
- •Общая физика
- •§ 1. Кинематика материальной точки и поступательного движения твердого тела
- •II закон Ньютона. Ускорение, приобретаемое материальной точкой (телом) пропорционально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точки (тела).
- •III закон Ньютона. Силы, с которыми действуют друг на друга тела, равны по модулю и противоположены по направлению.
- •2.2. Закон сохранения импульса (количества движения)
- •2.3. Энергия, работа, мощность
- •2.4. Закон сохранения и превращения энергии
- •2.5 Тяготение
- •2.6. Механика вращательного движения
- •Момент инерции, момент силы, момент импульса.
- •И вращательном движениях
- •2.7.Колебания и волны Механические колебания, математический маятник
- •2.8. Границы применимости законов классической механики и элементы специальной теории относительности
- •§ 1. Параметры термодинамических систем (параметры состояния)
- •§ 2. Законы идеальных газов
- •§ 3. Уравнение состояния реальных газов
- •Уравнение ван-дер-ваальса или уравнение состояния реальных газов
- •§4. Основы термодинамики.
- •Кинетической теории идеальных газов
- •Наиболее вероятная (максимальная)
- •§1. Электрическое поле
- •§1.1. Силовые характеристики электрического поля
- •§1. 2. Энергетические характеристики электрического поля
- •§1.3. Диполь
- •§1.4. Проводники в электрическом поле
- •§1.5. Диэлектрики в электрическом поле
- •§1.6. Электроемкость
- •§1.7. Конденсаторы
- •§1.8. Энергия электростатического поля
- •§2.1. Электродвижущая сила (эдс) (e ) источника
- •§2.2. Закон Ома для постоянного тока
- •§2.3. Закон Джоуля-Ленца
- •§2.4. Правила Кирхгофа (1847г.)
- •§2.5. Зонная теория
- •Гл. 3 электромагнетизм
- •§3.1. Характеристики магнитного поля
- •И мп на оси кругового тока.
- •§3.2. Вещество в магнитном поле
- •§3.3. Рамка с током в магнитном поле (Применения закона Ампера)
- •§3.4. Сила Лоренца
- •§3.5. Движение заряженных частиц в электрическом поле
- •§3.6. Движение заряженных частиц в магнитном поле
- •§ 3.7. Электромагнитная индукция: Закон Фарадея − Ленца
- •§3.8. Закон Ома для полной цепи
- •§3.9. Индуктивность, самоиндукция, взаимная индукция
- •1 Гн индуктивность такого контура, магнитный поток самоиндукции которого при токе 1 а равен 1 Вб.
- •§3.10. Энергия магнитного поля
- •§4.1. Полное сопротивление цепи при переменном токе.
- •§4.2. Резонанс
- •Шкала электромагнитных волн
- •§1.1. Поглощение света (Закон бугера)
- •§1.2. Законы геометрической оптики
- •§1.3. Формула призмы
- •§1.4. Линзы
- •Характер изображения собирающей линзы
- •§1.5. Аберрации или погрешности оптических систем
- •§2. Волновая оптика
- •§2.1. Интерференция света
- •§2.2. Дифракция света
- •РешеткаУсловияУсловия§2.3. Дисперсия света и спектральный анализ
- •§ 2.4. Поляризация света
- •Объяснение законов отражения и преломления с точки зрения волновой теории
- •§1. Тепловое излучение
- •Закон Стефана - Больцмана. Полная (по всему спектру) излучательная способность абсолютного черного тела прямо пропорциональна четвертой степени его абсолютной (термодинамической) температуре т:
- •§ 2. Фотоэффект
- •§ 3. Строение вещества
- •§ 3.1. Модели атома Резерфорда
- •§ 3.2. Постулаты Бора
- •§ 3.3. Правила отбора Паули, квантовые числа и таблица Менделеева
- •Периодическая система элементов Менделеева и распределение электронов по подоболочкам
- •§ 3.4. Радиоактивность
- •Закон радиоактивного распада
- •§ 3.5. Физика атомного ядра
- •§ 3.6. Элементарные и фундаментальные частицы
- •Классификация частиц
- •§3.7. Волновые свойства микрочастиц
- •§3.8. Соотношение неопределенности Гейзенберга
- •§3.9. Основы квантовой механики.
- •Основная литература
- •Вспомогательная литература
- •Контрольные вопросы по физике Трофимова т.И., Курс физики, «Высшая школа»,2000г.
- •Применение первого начала термодинамики к термодинамическим изопроцессам
- •Приложение к теме «Оптика» основные фотометрические величины и их единицы
§1.6. Электроемкость
Физическую величину, характеризующую способность проводника накапливать на себе заряды, называется электрической ёмкостью (электроемкостью).
Если уединенному
проводнику сообщить разное количество
зарядов q1,
q2,
q3,…qn,
то у него
появиться потенциалы φ1,
φ2,
φ3,…
φn,
но при этом всегда
![]() (т.е.
φ ~ q
или q~
φ и q=С
φ).
(т.е.
φ ~ q
или q~
φ и q=С
φ).
Электроемкостью (С) называют отношение заряда уединенного проводника q к его потенциалу φ:
![]() .
.
Таким образом, электроемкость уединенного проводника численно равна заряду, изменяющему потенциал проводника на единицу.
Единица электроемкости
Фарад(Ф):
![]() .
.
Размерность электроемкости [C]=[q]/[φ]=м-2кг-1с4А2.
С зависит от размеров и форм проводника,
но не зависит от материала и его
агрегатного состояния. Для геометрически
подобных проводниках С
прямо
пропорционально их
линейным размерам. Например, т.к. для
шара на расстояние r
от точечного заряда и на поверхности
однородного шара с радиусом
r
потенциал
поля φ
один и тот же, тогда из потенциала
точечного заряда q
(
зависит от размеров и форм проводника,
но не зависит от материала и его
агрегатного состояния. Для геометрически
подобных проводниках С
прямо
пропорционально их
линейным размерам. Например, т.к. для
шара на расстояние r
от точечного заряда и на поверхности
однородного шара с радиусом
r
потенциал
поля φ
один и тот же, тогда из потенциала
точечного заряда q
(![]() ),
получаем
),
получаем
C=4π ε0 ε r.
(Кстати, отсюда
![]() ,
,
![]() и [ε0]
= фарад на метр)
и [ε0]
= фарад на метр)
А также
![]() .
.
Для вакуума ε=1, при С=1Ф и ε0 =8,85.10-12ф/м, получаем, что r ≈ 9.106!
Т. е. 1Ф – чрезвычайно большая единица электроемкости, поэтому применяются его миллионные и более мелкие части фарада:
1 микрофарад (мкф) =10-6 фарад, что соответствует r =9 км;
1 пикофарад (пф) = 10-6 мкф =10-12 ф, что соответствует r =0,9 см.
У Земли (R ≈ 6400 км), С = 711мкф).
Т.к. в природе нет уединенных проводников, то в широком смысле электроемкость определяется как взаимная электроемкость (или взаимная емкость) между двумя проводниками:
![]()
Для двух проводников взаимная электроемкость – это физическая величина, численно равная заряду q, который нужно перенести из одного проводника на другой для того, чтобы изменить на единицу разность потенциалов между ними: φ1 и φ2 потенциалы этих проводников. Для уединенных проводников считается, что второй проводник находится в бесконечности, т.е. φ2 =0.
§1.7. Конденсаторы
Как мы убедились уединенные проводники с большими С имеют большие размеры. Но существуют системы (конденсаторы), которые дают большие С при малых размерах.
Конденсатор – это система двух близких расположенных проводников (обкладок), разделенных слоем диэлектрика.
В зависимости от формы обкладок конденсаторы делят на плоские (обкладки – две плоские пластины), цилиндрические (обкладки – два коаксиальные цилиндры) и сферические (обкладки – две концентрические сферы).
У простейшего плоского конденсатора электрическое поле внутри обкладок однородна; E=const.
П ри
зарядке одной из обкладке сообщается
некоторый +q
заряд, а другую обкладку заземляют: на
второй обкладке собирается равный q
, но противоположный по знаку заряд.
ри
зарядке одной из обкладке сообщается
некоторый +q
заряд, а другую обкладку заземляют: на
второй обкладке собирается равный q
, но противоположный по знаку заряд.
Из
![]() ,
учитывая, что q=σS,
φ1
–φ2=Ed
и
,
учитывая, что q=σS,
φ1
–φ2=Ed
и
![]() (см. пример эл. поля между двумя
параллельными плоскостями), получаем
формулу плоского конденсатора:
(см. пример эл. поля между двумя
параллельными плоскостями), получаем
формулу плоского конденсатора:
![]() .
.
Если обкладки имеют разные площади или частично перекрываются, то под S подразумевается меньшая или покрывающаяся часть площади.
Иногда роль диэлектрика играет пропарафинированная бумага.
Для всех типов конденсаторов существует пробивное напряжение Δφ - при котором происходит электрический разряд через слой диэлектрика.
Для сферического
конденсатора
![]() ,
где r1 и r2
радиусы сфер. Когда r2
- r1=Δr
<< r1=
r2 =r,
тогда
,
где r1 и r2
радиусы сфер. Когда r2
- r1=Δr
<< r1=
r2 =r,
тогда
![]()
Для цилиндрического
конденсатора
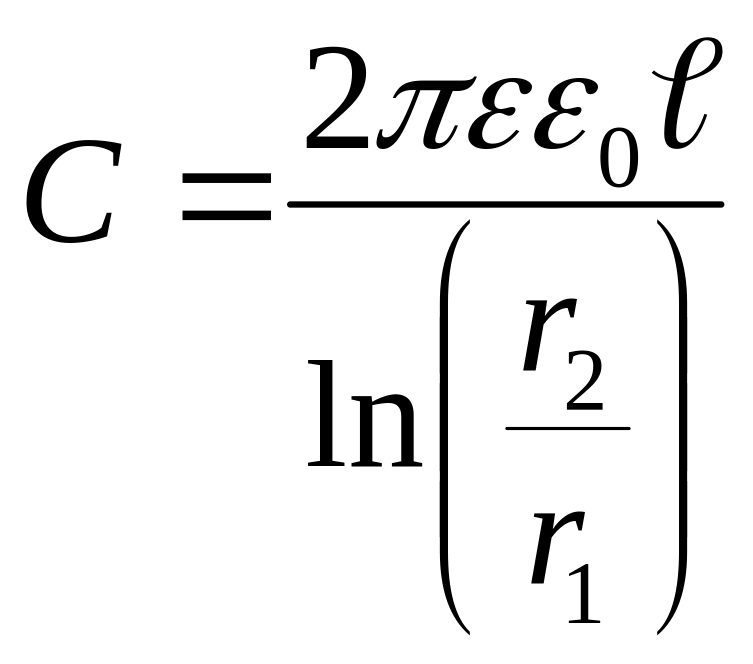 ,
где r1 и r2
радиусы оснований цилиндров, а ℓ-
его высота.
,
где r1 и r2
радиусы оснований цилиндров, а ℓ-
его высота.
Такой конденсатор с С = 10 мкф имеет размер спичечного коробка. (Металлический шар имел бы R ≈ 90 км).
В конденсаторе с переменной С применяются газообразные или жидкие диэлектрики.
Существуют Многопластинчатые конденсаторы, для которых
![]() или
или
![]() ,
,
где k - число промежуток, n - число пластинок, а d – расстояние между пластинок.
Вне конденсатора электрическое поле почти отсутствует (Е=0).
Соседние проводники уже не влияют на С конденсатора.
Конденсаторы можно рассматривать как накопители электрической энергии.
Батареи из конденсаторов
При параллельном соединении конденсаторов полная электроемкость равна сумме электроемкостей отдельных конденсаторов.
![]()
 ,
,
![]() ,
,
![]()
![]()
![]()
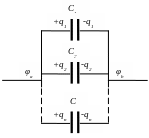
П ри
последовательном соединении
конденсаторов величина обратная величине
полной электроемкости, равна сумме
величин, обратных электроемкостей
отдельных конденсаторов.
ри
последовательном соединении
конденсаторов величина обратная величине
полной электроемкости, равна сумме
величин, обратных электроемкостей
отдельных конденсаторов.
Заряды всех обкладок одинаковы и равны q, тогда
Δφ = φ1- φn=(φ1 – φ2)+(φ2 – φ3)+…+(φn-1 – φn)
![]()
![]() .
Например, при n=2,
.
Например, при n=2,
![]() .
.
Биологические конденсаторы у некоторых рыб (электрический скат, электрический угорь и др.) имеют довольно большие электроемкости, и у них напряжение может достигнуть Δφ~1000B, а мощность W~1квт . Они состоят из проводящей (нервной) и непроводящей (соединительной) ткани.
Измеряя С конденсатора с исследуемым диэлектриком и без него, можно определить диэлектрическую проницаемость диэлектрика из соотношения ε=С/С0.
