Критерий окончания итерационного процесса
При заданной точности e>0 вычисления следует вести до тех пор, пока не окажется выполненным неравенство: ½xn – xn-1½<e
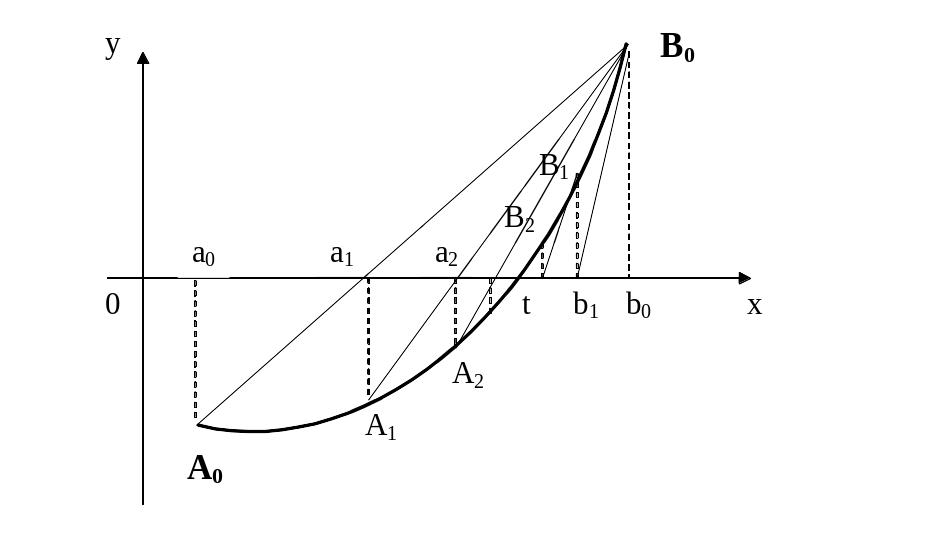
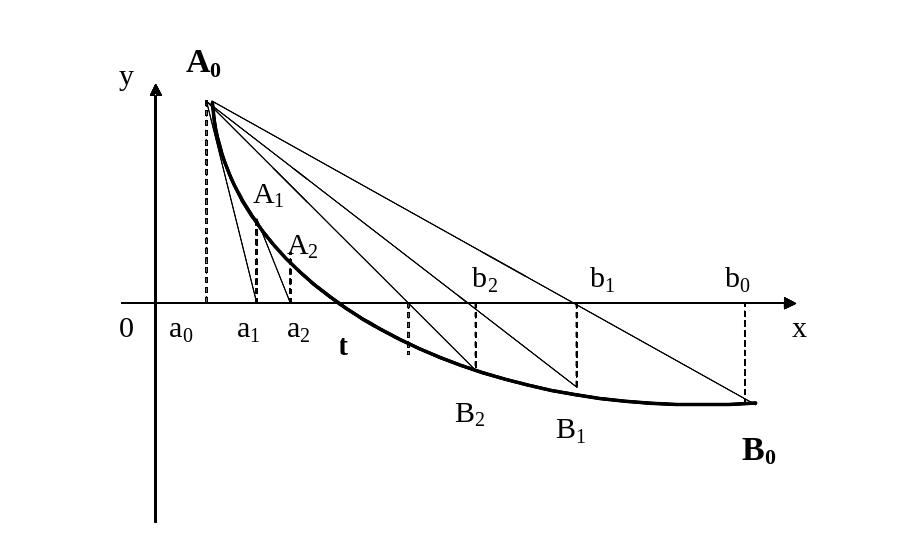
Комбинированный метод хорд и касательных.
Метод хорд и метод касательных часто применяют в сочетании друг с другом.
Пусть дано уравнение f(x)=0, корень t отделен и находится на отрезке [a,b]. Применим комбинированный метод хорд и касательных.
Если f¢(x)×f²(x)>0, то метод хорд дает приближение корня с недостатком, а метод касательных с избытком.
Е
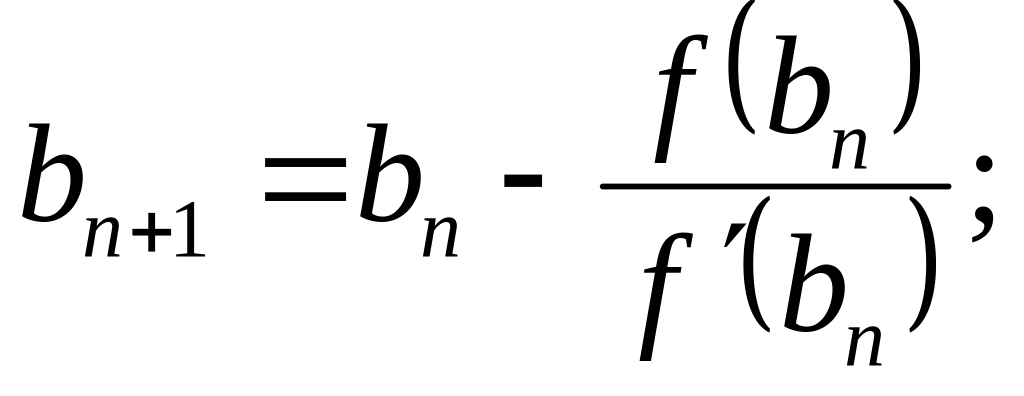сли
f¢
(x)×
f²
(x)>0:
f¢ (x)× f² (x)<0:
Если f¢ (x)× f² (x)<0:
П
роцесс
вычислений прекращается, как только
будет выполнено неравенство:
В
качестве приближенного значения корня
можно взять середину этого отрезка:
Метод итераций
Заменим уравнение f(x)=0 равносильным ему – x=j(x). Требуется найти вещественный корень этого уравнения на отрезке [a,b]. Возьмем произвольную точку x0 из области определения функции j(x) и будем строить последовательность чисел с помощью рекуррентной формулы xn+1=j(xn), т.е. x1=j(x0), x2=j(x1), x3=j(x2) и т.д.
Итерационная последовательность {xn} :
1)сходится, т.е. имеет предел, равный корню уравнения f(x)=0 или
2) расходится, т.е. не имеет предела.
Теорема о сходимости итерационной последовательности
П
усть
на отрезке [a, b] имеется единственный
корень уравнения x=j(x)
и во всех точках этого отрезка j¢
(x) удовлетворяет неравенству: új¢
(x)ú
£
q<1. Если при этом выполняется и условие
a£
j(x)£
b, то итерационный процесс сходится и
за нулевое приближение x0
можно взять любое число из отрезка
[a,b].
Чем меньше
- угловой коэффициент касательной, тем лучше сходимость итерационного процесса.
Критерий окончания итерационного процесса
Е
сли
поставить условие, что истинное значение
корня должно отличаться от приближенного
значения на величину e,
т.е. , то приближения
надо вычислять до тех пор пока будет
выполнено неравенство:
или ,
г
де
q
определяется из соотношения:
Задачи с решениями
Задача 1
Отделить корни
уравнения
аналитическим методом.
Решение Найдем первую производную функции
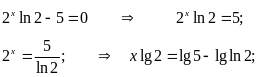
Знаки функции:
-
x
- ∞
2
3
+ ∞
f(x)
+
-
-
+
Знак меняется дважды, следовательно, уравнение имеет два корня.
Более мелкие интервалы:
-
x
-1
0
1
2
3
4
5
f(x)
+
-
-
-
-
-
+
Корни уравнения заключены в пределах (-1;0) и (4,5).
Задача 2
Методом хорд
уточнить до e=0,001
меньший корень уравнения
Корни отделены и
меньший содержится на отрезке
Решение:
Процесс
последовательного приближения к корню
следует продолжать до тех пор, пока не
будет выполнено условие
.
Определить знак второй производной:
Значит, за неподвижный
конец отрезка нужно принять
Тогда вычисления по формулам (3), (4), где
и
Если записать (4) в виде:
,
то сразу же можно будет получить разность
между последними приближениями и
проверять выполнение неравенства
Задача 3:
Найти методом касательных приближенное значение корня уравнения
f(x) = x - cosx = 0
на интервале [0,5;1].
Решение:
Рекуррентная формула метода касательных принимает в данном случае вид:
Выберем в качестве нулевого приближения x0=0,5 и подсчитаем следующие приближения. Результаты вычислений приведены в таблице:
N |
xn |
0 |
0,500000000000 |
1 |
0,755222417106 |
2 |
0,739141666150 |
3 |
0,739085133921 |
4 |
0,739085133215 |
5 |
0,739085133215 |
После двух шагов мы достигли точности 10-4
З
адача
4:
Р
ассмотрим
вычисление как задачу решения
уравнения: x2
- a
= 0 в области
x>0.
Написать для вычисления корня уравнения
итерационную последовательность по
методу касательных. Вычислить с её
помощью .
Р
ешение:
Р
екуррентная
формула метода касательных для уравнения
принимает вид:
(*)
П ерейдём к вычислению .
В
спомним,
что .
Выбирая x0=2, делаем несколько итераций по формуле (*):
x
0=2;
x1=1,5;
Третий шаг определяет
с погрешностью:
Задача 5:
Н
айти
приближенное значение корня на отрезке
[0,1] методом итераций
Р
ешение:
Н
а
отрезке [0,1]
т .е. выполняется условие
г
де
q=0,85.
П
ринимаем
за
(середина
отрезка)
Т
огда
,
, и т.д.