Степенной базис
Выберем
базисные функции
в виде последовательности степеней
аргумента
,
которые линейно независимы.
(8)
В
этом случае также как и при интерполяции,
мы будем аппроксимировать экспериментальную
зависимость полиномом. Однако степень
полинома
выбираем обычно
(при лангранжевой интерполяции
).
Аппроксимирующая кривая в МНК не проходит
через значения исходной функции в узлах,
но проведена из условия наименьшего
суммарного квадратичного отклонения.
Экспериментальные данные “сглаживаются“
с помощью функции
.
Если же выбрать
,
то на основании единственности
интерполяционного полинома получим
функцию
,
совпадающую с каноническим интерполяционным
полиномом степени
,
аппроксимирующая кривая пройдет через
все экспериментальные точки и величина
будет равна нулю. Последнее обстоятельство
используется для отладки и тестирования
программ, реализующих алгоритмы МНК.
Запишем расширенную матрицу системы нормальных уравнений для базиса:
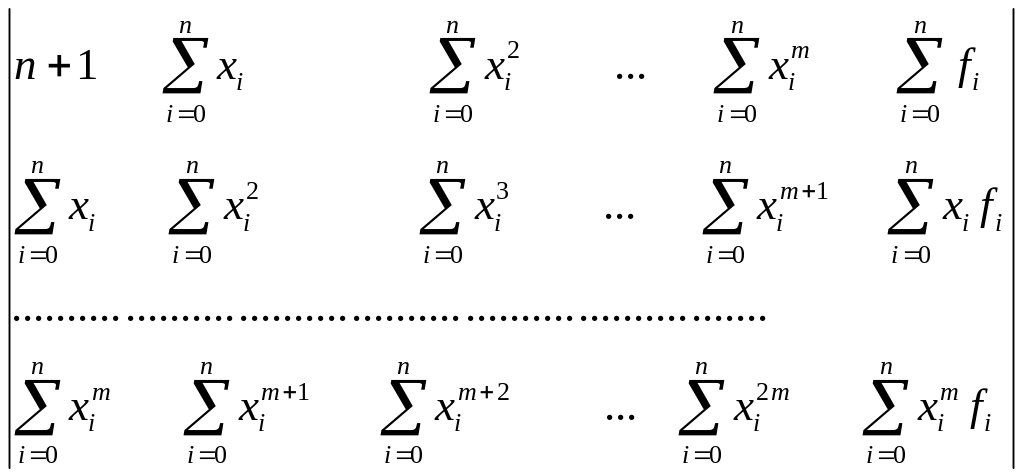(9)
Нетрудно видеть, что для формирования расширенной матрицы (9) достаточно вычислить только элементы первой строки и двух последних столбцов, остальные элементы не являются “оригинальными” и заполняются с помощью циклического присвоения.
Р
ешение
данной задачи показано в следующем
фрагменте рабочего листа Excel,
на примере аппроксимации данных о
количестве осадков степенным полиномом
второго порядка. Для того, чтобы посмотреть
какие формулы введены в ячейки таблицы,
щелкните два раза <ЛК> мыши по
приведенному фрагменту.