1.Высокие температуры(kT h )

Разложим в ряд знаменатель:

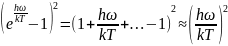
В числители:

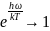
Тогда:

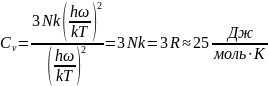
Т.е. при высоких температурах значение теплоемкости приводит к закону Дюлонга и Пти.

2.Низкие температуры (kT h )

В этом случаи и в знаменателе единицей можно пренебречь, тогда

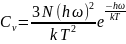
Как следствие из этого выражения при стремлении температуры твердого тела к 0, экспоненциальный множитель оказывается преобладающим, так что теплоемкость стремится к 0 по закону .

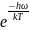Основной причиной убывания теплоемкости является то, что при низких температурах закон равномерного распределения энергии по степеням свободы становится несправедливым.

Средняя энергия осциллятора 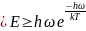при kT h экспоненциально быстро падает до 0 при температуре, стремящейся к 0, в то время как в соответствии с законом равномерного распределения она падает до нуля линейно. Таким образом, модель Эйнштейна действительно хорошо описывает факт резкого уменьшения теплоемкости при низких температурах при надлежащем подборе частоты осциллятора .

Температура, при которой начинается быстрый спад теплоемкости и получившая название характеристической температуры Эйнштейна(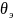 ), очевидно, определяется близостью к :

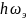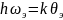
если положить 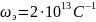; ;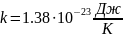 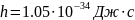, то

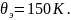
Реальная температура Эйнштейна зависит от свойств веществ, для большинства твердых тел она порядка 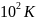, но есть вещества(бериллий, алмаз), у которых аномально высока(выше 1000К).

Характеристическая температура является одной из важнейших характеристик кристалла. При температурах ниже характеристической 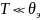необходимо квантовое рассмотрение.

При 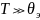квантование энергии можно не учитывать и рассмотрение вести исходя из обычных классических представлений.

Теория Дебая

Дебай учел, что колебания атомов в кристаллической решетки не являются независимыми. Смещение одного из атомов из положения равновесия влечет за собой смещение других соседних с ним атомов. Таким образом, кристалл представляет собой систему N упруго связанных друг с другом атомов, обладающую s=3N степенями свободы.

Произвольное колебание струны является суперпозицией гармонических стоячих волн. Следовательно, каждое нормальное колебание струны представляет собой стоячую волну.

Аналогично, каждому нормальному колебанию кристаллической решетки соответствует стоячая волна, устанавливающаяся в объеме кристаллического тела. Действительно, из-за связи между атомами колебание, возникающее в каком-то месте кристалла, передается от одного атома к другому, в результате чего возникает упругая волна. Дойдя до границы кристалла волна отражается. При положении прямой и отраженной волн образуется стоячая волна. Стоячие волны могут возникать для частот(или длин волн), удовлетворяющих определенным условием. Если взять кристаллическое тело в виде параллелепипеда со сторонами a,b,c, то эти условия выражаются формулами:

, ,

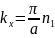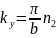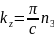
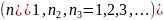
Где 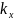, ,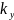 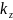-проекции волнового вектора по оси x,y,z.

Число стоячих волн, т.е. нормальных колебаний, частоты которых заключены в интервале от 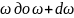, определяется выражением:

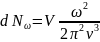
где -фазовая скорость волны в кристалле.

Данная формула не учитывает возможных видов поляризации волны. В твердой среде вдоль некоторого направления могут распространяться три разные волны с одним и тем же значением , отличающиеся направлением поляризации: одна продольная и две поперечные с взаимно перпендикулярными направлениями колебаний.

В соответствии с этим значением запишем предыдущую формулу, как

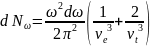(1)

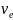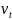Где -фазовая скорость продольных волн, а -фазовая скорость поперечных упругих волн. Положим для простоты, что 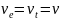. Тогда

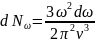(2)

Максимальную частоту 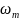нормальных колебаний решетки можно найти, приравняв полное число колебаний к числу степеней свободы, равному 3n (n- число атомов в единице объема кристалла):

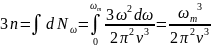I

Отсюда:

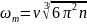(3)

Тогда наименьшая длина волны, возбуждаемая в кристалле равна:

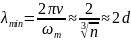
где 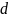- расстояние между соседними атомами в решетке. Этот результат согласуется с тем, что волны, длина которых меньше удвоенного межатомного расстояния, не имеют физического смысла.

Исключив из равенств (2) и (3) скорость 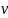, получим для числа нормальных колебаний 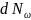в интервале частот 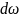, приходящегося на единицу объема кристалла, следующее выражение:

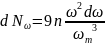(4) II

Внутренняя энергия единицы объема кристалла может быть представлена в виде

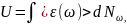
где 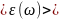-среднее значение энергии нормального колебания частоты . Подставив выражение 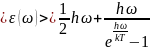и (4) для , придем к формуле:

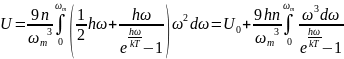(5)

Здесь 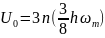-энергия нулевых колебаний кристалла.

Производная от U по T дает теплоемкость единицы объема кристалла:

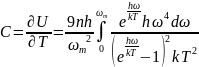
Величину 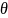, определяемую условием: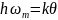 , называют характеристической температурой Дебая. По определению,

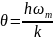(6)

Температура Дебая указывает для каждого вещества ту область, где становится существенным квантование энергии колебаний.

Введем переменную 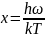. III

Тогда выражение для теплоемкости примет вид

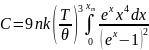(7)

где .
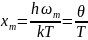