2. Динамика материальной точки Основные определения и формулы

Первый закон Ньютона – закон инерции: материальная точка сохраняет состояние покоя или равномерного прямолинейного движения при отсутствии воздействия внешних сил . Служит для определения инерциальной системы отсчета (ИСО).

Второй закон Ньютона

(2.1)

где – равнодействующая всех сил, приложенных к материальной точке массы , – импульс материальной точки.

Свойство силы быть скоростью изменения импульса является общим для сил любой природы и поэтому может служить определением силы. Обратите внимание на то, что импульс обладает тем удивительным свойством, что его изменение не зависит от величины самого импульса:

.

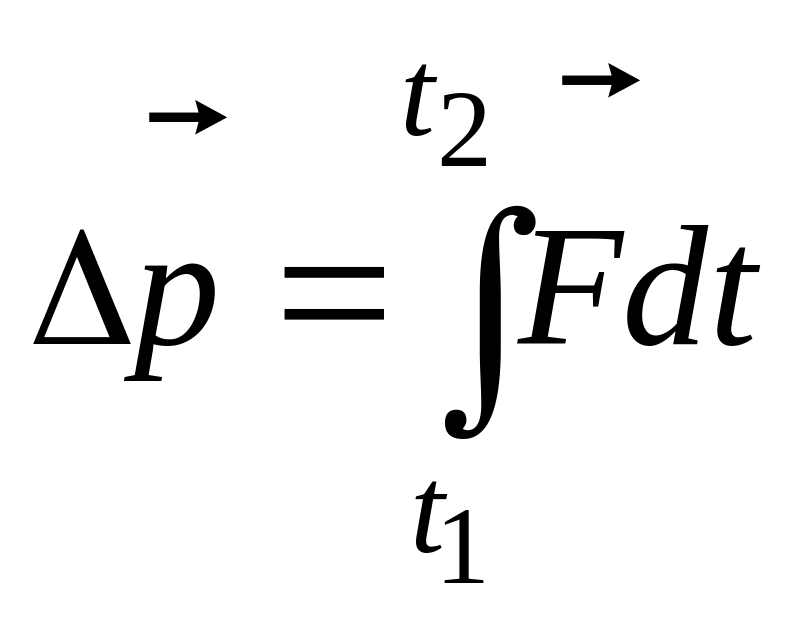Второй закон можно записать иначе:

или

, (2.2)

где – ускорение.

Здесь предполагается, что ускорение не зависит от скорости тела и направлено всегда вдоль силы . Это утверждение справедливо лишь при .

Третий закон – в ИСО тела (материальные точки) взаимодействуют с силами, равными по модулю и противоположными по направлению:

, (2.3)

где и – силы взаимодействия двух тел (они приложены к разным телам). В неинерциальной системе отсчета (НСО) второй закон Ньютона имеет вид

(2.4)

Здесь – сила инерции; – ускорение неинерциальной системы отсчета относительно инерциальной; ускорение тела в неинерциальной системе отсчета.

Сила трения скольжения

(2.5)

где – коэффициент трения скольжения, – сила нормальной реакции опоры.

Упругая сила

(2.6)

где – величина упругой деформации, – коэффициент упругости.

Суммарный импульс системы материальных точек

. (2.7)

Закон сохранения импульса (ЗСИ): в ИСО полный импульс замкнутой системы материальных точек сохраняется:

. (2.8)

Работа, совершаемая силой ,

. (2.9)

Мощность силы

. (2.10)

Кинетическая энергия частицы массой , движущейся со скоростью ,

. (2.11)

Изменение кинетической энергии материальной точки (теорема о кинетической энергии)

(2.12)

где – работа всех сил, действующих на материальную точку.

Работа сил потенциального поля (консервативных сил) определяется уменьшением потенциальной энергии системы:

. (2.13)

Соотношение между силой и потенциальной энергией частицы в поле

в декартовых координатах

. (2.14)

Потенциальная энергия тела, поднятого на высоту вблизи поверхности Земли,

(2.15)

Потенциальная энергия упруго-деформированного тела с коэффициентом жёсткости

(2.16)

где величина деформации.

Сумма потенциальной и кинетической энергий называется полной механической энергией:

(2.17)

Закон сохранения механической энергии (ЗСЭ): В ИСО полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной:

const. (2.18)

В общем случае изменение полной механической энергии системы

(2.19)

где А_внеш – работа внешних сил; А_{внутр неконс} – работа внутренних неконсервативных сил.

Закон всемирного тяготения:

(2.20)

где и – массы материальных точек, – расстояние между ними, – гравитационная постоянная, сила направлена вдоль прямой, соединяющей массы и .

Ускорение свободного падения в поле тела массы (по аналогии с электростатическим полем является напряженностью гравитационного поля) на расстоянии от него:

(2.21)

Потенциальная энергия гравитационного взаимодействия двух материальных частиц на расстоянии :

(2.22)

Принцип суперпозиции сил (полей): результат воздействия на частицу нескольких внешних сил есть просто сумма результатов воздействия каждой из сил. Без этого принципа невозможно решить задачу о взаимодействии более чем двух тел. Это очень общий принцип физики, выходящий далеко за пределы механики.

Принцип относительности Галилея: законы механики инвариантны относительно преобразований Галилея.