
- •Л.И. Васильева, н.А. Иванова, д.Л. Федоров, с.Н. Соколова механика пособие к решению задач
- •1. Кинематика поступательного движения материальной точки. Кинематика вращательного движения абсолютно твердого тела Основные определения и формулы
- •Методические указания
- •Примеры решения задач
- •2. Динамика материальной точки Основные определения и формулы
- •Методические указания
- •Примеры решения задач
- •3. Динамика твердого тела Основные определения и формулы
- •Методические указания
- •Примеры решения задач
- •Законы сохранения момента импульса и энергии
- •Примеры решения задач
- •Поступательного и вращательного движений
- •Механика
- •190005, С.-Петербург, 1-я Красноармейская ул., д.1
Л.И. Васильева, н.А. Иванова, д.Л. Федоров, с.Н. Соколова механика пособие к решению задач
Министерство образования и науки Российской Федерации
Балтийский государственный технический университет “Военмех”
Л.И. Васильева, Н.А. Иванова, Д.Л. Федоров, С.Н. Соколова
МЕХАНИКА
Пособие к решению задач
Под редакцией Н.А. Ивановой
Санкт-Петербург
2010
УДК 531/.534(076)
М55
Механика:
пособие к решению задач /
Л.И.
Васильева [и др.]; под ред. Н.А. Ивановой;
Балт. гос. техн. ун-т. – СПб., 2010. – 65 с.
ISBN
978-5-85546-568-6
Кратко
изложены необходимые теоретические
сведения по механике. Подробно разобраны
решения ряда типовых задач.
Предназначено
для студентов 1-го курса всех технических
специальностей
М55
УДК 531/.534(076)
Р е ц е н з е н т В.В. Лентовский
Утверждено
редакционно-издательским
советом университета
ISBN 978-5-85546-568-6 © Авторы, 2010
© БГТУ, 2010
1. Кинематика поступательного движения материальной точки. Кинематика вращательного движения абсолютно твердого тела Основные определения и формулы
Вектор перемещения
![]() – вектор, направленный из “начальной”
точки траектории в “конечную” (за
данный интервал времени ∆t).
– вектор, направленный из “начальной”
точки траектории в “конечную” (за
данный интервал времени ∆t).
Длина пути
![]() – длина траектории между выбранными
точками.
– длина траектории между выбранными
точками.
Средняя скорость
![]() ср
ср![]() (1.1)
(1.1)
Мгновенная или истинная скорость
![]() (1.2)
(1.2)
Вектор мгновенной скорости направлен в каждой точке траектории по касательной к траектории.
Модуль мгновенной скорости
![]() (1.3)
(1.3)
Ускорение
![]() (1.4)
(1.4)
Криволинейное движение
Вектор полного ускорения (рис. 1.1)
![]()
его модуль
![]()
 (1.5)
(1.5)
где
![]() – нормальное (центростремительное)
ускорение, направлено перпендикулярно
вектору скорости и отвечает за изменение
ее направления.
– нормальное (центростремительное)
ускорение, направлено перпендикулярно
вектору скорости и отвечает за изменение
ее направления.
Любое криволинейное
движение происходит при наличии
![]() ,
модуль которого
,
модуль которого
![]() ,
(1.6)
,
(1.6)
где R – радиус кривизны траектории.
![]() – тангенциальное
или касательное ускорение, направленное
вдоль вектора скорости и ответственное
за изменение ее модуля. Модуль
тангенциального ускорения
– тангенциальное
или касательное ускорение, направленное
вдоль вектора скорости и ответственное
за изменение ее модуля. Модуль
тангенциального ускорения
![]() (1.7)
(1.7)
Путь,
пройденный телом за время
![]()
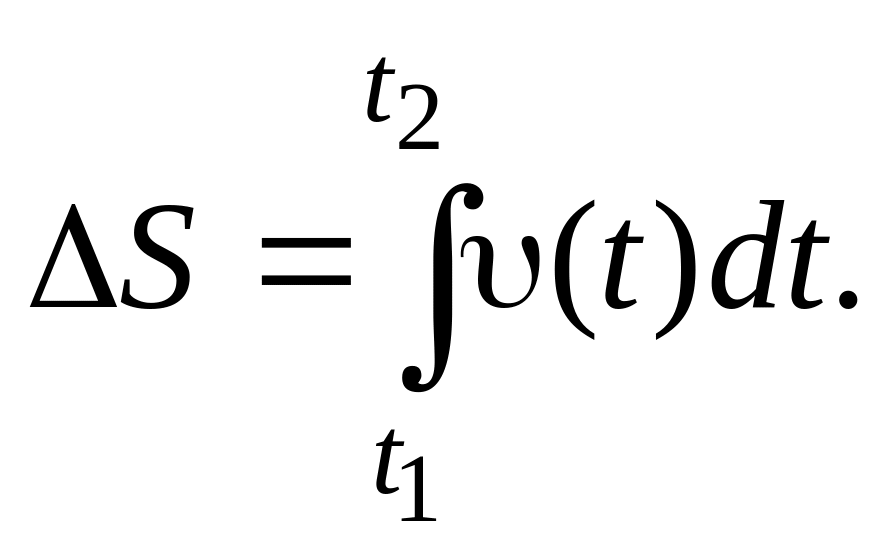 (1.8)
(1.8)
Вектор перемещения
за
![]() при
при
![]() =
const
=
const
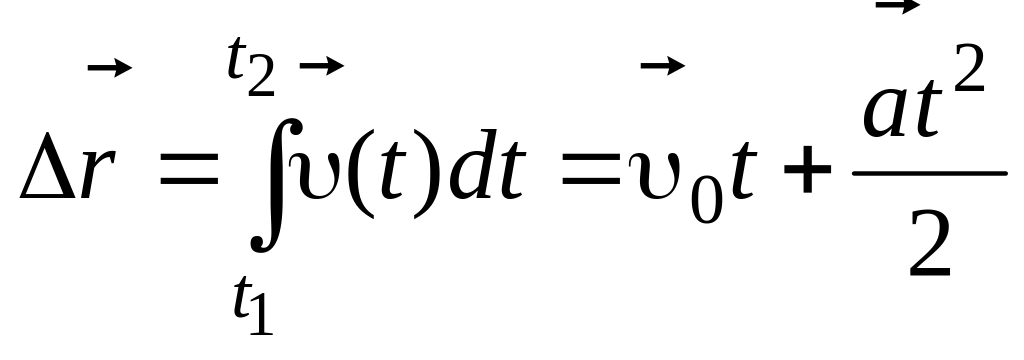 . (1.9)
. (1.9)
Изменение вектора
скорости за
![]()
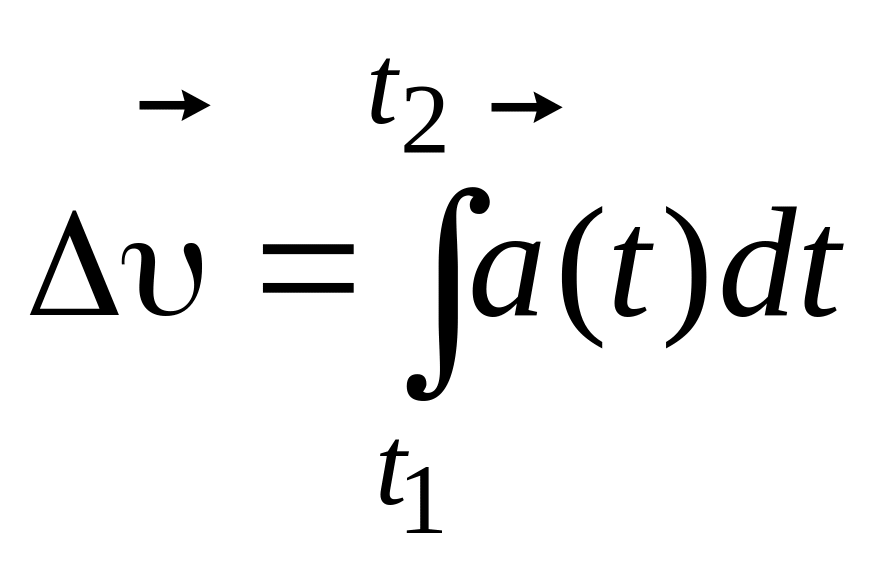 . (1.10)
. (1.10)
Тогда, при
![]() ,
зависимость
,
зависимость
![]() от времени
от времени
![]()
![]() . (1.11)
. (1.11)
Угловая скорость (рис. 1.2)
![]()
 (1.12)
(1.12)
где
![]() – вектор углового перемещения,
направленный вдоль оси вращения
– вектор углового перемещения,
направленный вдоль оси вращения
![]() по правилу правого винта. (Обратите
внимание на то, что угловая скорость
направлена тоже вдоль оси вращения по
правилу правого винта.)
по правилу правого винта. (Обратите
внимание на то, что угловая скорость
направлена тоже вдоль оси вращения по
правилу правого винта.)
Угловое ускорение
![]() (1.13)
(1.13)
В
случае закрепленной оси вектор углового
ускорения направлен вдоль оси: по
направлению вектора угловой скорости
![]() ,
если вращение ускоренное, и против
вектора
,
если оно замедленное.
,
если вращение ускоренное, и против
вектора
,
если оно замедленное.
Угол поворота за
при
![]() можно рассчитать по формуле
можно рассчитать по формуле
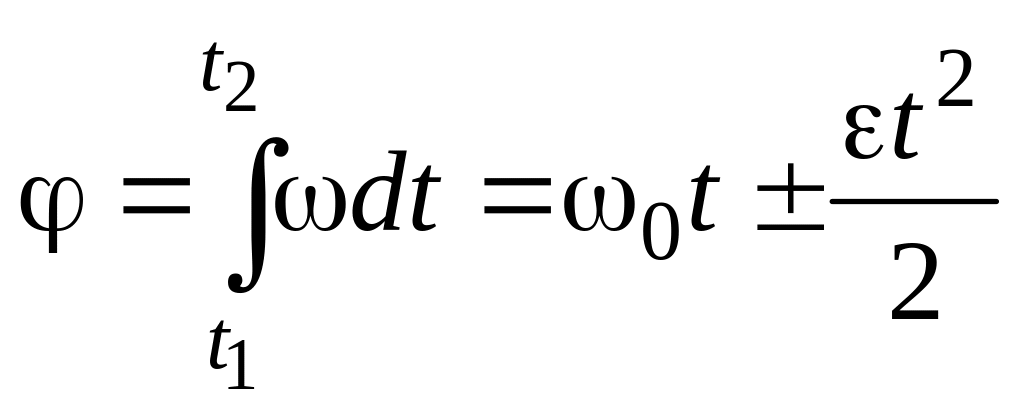 . (1.14)
. (1.14)
Изменение угловой скорости за
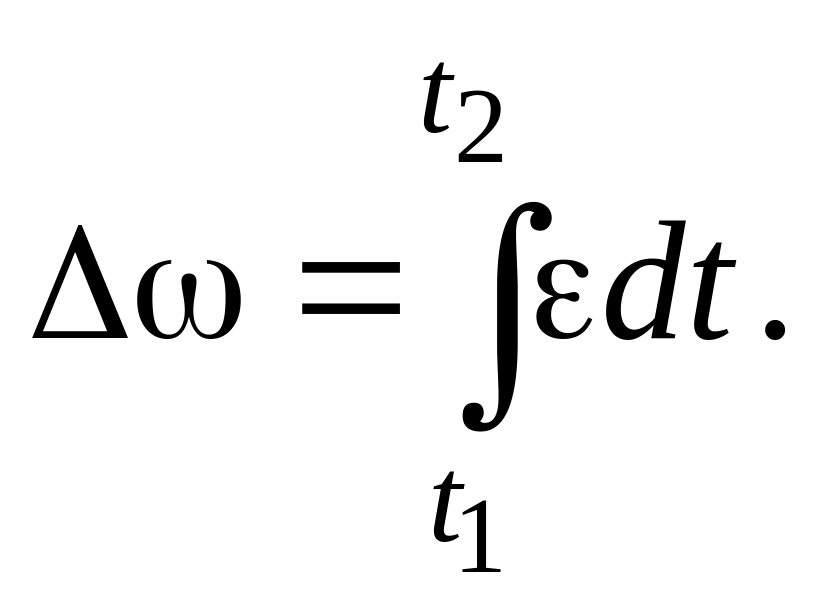
Тогда, при ,
![]() . (1.15)
. (1.15)
Связь между угловыми характеристиками вращающегося тела и линейными характеристиками движения его точек осуществляется следующими отношениями:
![]() (1.16)
(1.16)
![]() (1.17)
(1.17)
![]() (1.18)
(1.18)
![]() (1.19)
(1.19)
В случае неподвижной оси вращения эти соотношения принимают вид
![]() (1.20)
(1.20)
![]() (1.21)
(1.21)
![]() (1.22)
(1.22)
![]() (1.23)
(1.23)
где
![]() – расстояние точки тела до оси вращения.
– расстояние точки тела до оси вращения.
Тело, относительно которого рассматривается движение, и связанная с ним система координат и система отсчёта времени образуют систему отсчета. Любой закон физики может быть записан математически лишь относительно определенной системы отсчета.
