12.4Обработка результатов измерений

1. По результатам измерений в п. 1 (табл. 6,1) вычислить параметры индуктивной катушки, резистора и конденсатора на частоте первой гармоники. Результаты записать в графы «вычислено» табл. 6,1.

2. По виду периодического несинусоидального напряжения и его параметрам (п. 3) разложить входное напряжение в ряд Фурье (до пятой гармоники) и определить параметры гармоник. По действующим значениям гармоник входного напряжения определить его действующее значение. Результат записать в строке «вычислено» для соответствующей цепи (табл. 6.2).

3. По известному входному напряжению (его гармоническому составу) и параметрам цепи (табл. 6.1) рассчитать соответствующие цепи и определить действующие значения токов и напряжений элементов электрической цепи, а также определить активную мощность всей цепи. Результаты расчета записать в графы «вычислено» табл. 6.2.

4. Сравнить кривые токов в ветвях цепей №1 и №2 и объяснить влияние параметров реактивных элементов и мест их включения на форму токов.

12.5Контрольные вопросы и задания

1. Определить, какой вид примет ряд Фурье, если f(ωt) = f(–ωt)?

2. Каким видом симметрии обладает кривая, заданная в виде i = 5Sin(ωt) + 3Sin(ωt)?

3. Определить мгновенное и действующее значения тока в цепи, если i = 3 + 4Sin(ωt)?

4. Как измениться действующее значение тока в последовательной R – L – C цепи, если значение индуктивности будет увеличено в двое? К цепи приложено несинусоидальное напряжение U = 100 + 150Sin(ωt).

5. Как измениться действующее значение тока в последовательной R – L – C цепи, значение емкости будет увеличено вдвое? К цепи приложено несинусоидальное напряжение U = 50 + 100Sin(ωt).

6. Условие резонанса напряжений на k-ой гармоники. Последовательное соединение R – L – C (R = 10 Ом; X_L⁽¹⁾= 10 Ом; X_C⁽¹⁾ = 30 Ом). К цепи приложено напряжение U = 100 + 50Sin(3ωt). Определить мгновенное и действующее значение тока.

7. Условие резонанса токов на k-ой гармонике. Параллельное соединение двух ветвей: R₁ – L и R₂ – C (g₁⁽³⁾ = 0,2 См; g₂⁽³⁾ = 0,2 См; b_L⁽³⁾=b_C⁽³⁾=0,1 См). Определить ток в цепи (мгновенное и действующее значение), если к цепи приложено напряжение U = 50 + 10Sin(3ωt).

8. Как влияют параметры реактивных элементов на форму тока в неразветвленной части цепи при последовательном и параллельном их соединении?

13Лабораторная работа № 14

Переходные процессы в неразветвленной электрической цепи с источником постоянного напряжения

Цель работы – исследование переходных процессов в электрических цепях R – L, R – C и R – L – C при помощи электронного осциллографа, выяснение характера переходного процесса в зависимости от вида элементов цепи и величины их параметров.

13.1Основные положения

1) Подключение цепи с последовательным соединением резистивного и емкостного элемента к источнику постоянного напряжения (рис. 7.1).

Если при t = 0 – конденсатор емкостью C не заряжен, то при t ≥ 0 имеем режим заряда конденсатора через резистор .

Рисунок 7.1 – Электрическая схема подключения цепи RC к источнику постоянного напряжения

Для t ≥ 0 имеем

или

(7.1)

Решение уравнения (7.1) имеет вид:

(7.2)

Постоянная интегрирования А определяется из второго закона коммутации: U_C(0+) = U_C(0–) = 0 = U + A. Отсюда A = –U.

Тогда напряжение на конденсаторе изменяется по закону:

(7.3)

Ток в цепи заряда конденсатора

(7.4)

Величина RC = τ называется постоянной времени цепи. Она имеет размерность времени и характеризует скорость протекания переходного процесса. Графически τ равна величине, подкасательной к кривой тока i(t) или напряжения U_C(t). Переходный процесс может считаться практически завершенным через t = (3 ÷ 5)τ.

2) Короткое замыкание цепи R – C.

Пусть конденсатор с емкостью С, заряженный до напряжения U, в момент t = 0 подключается к резистору с сопротивлением R (рис. 7.2).

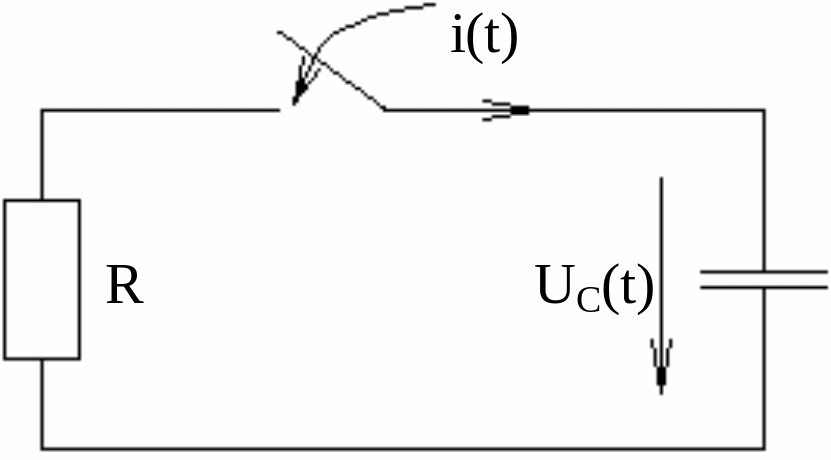
Рисунок 7.2 – Схема короткого замыкания цепи R – C

После замыкания ключа для цепи справедливо уравнение

(7.5)

решение которого, т.е. напряжение на конденсаторе, имеет вид:

(7.6)

Так при разряде конденсатора

(7.7)

3) Включение и короткое замыкание индуктивной катушки. Этот процесс подобно предыдущему описывается уравнением первого порядка и характеризуется постоянной времени . При подключении цепи R – L к источнику постоянного напряжении ток в цепи определяется выражением

, (7.8)

а напряжение на индуктивности

. (7.9)

Если ток в индуктивности до коммутации был равен i(0–)=U/R, то при коротком замыкании цепи R – L изменение тока будет определяться выражением

, (7.10)

а напряжение на индуктивности

. (7.11)

4) Подключение цепи с последовательным соединением R – L – C к источнику постоянного напряжения (рис. 7.3).

Рисунок 7.3 – Схема подключения цепи R – L – C к источнику постоянного напряжения

Пусть при t = 0 – напряжение на конденсаторе и ток в цепи до коммутации равно нулю. Это соответствует заряду конденсатора с емкостью С через резистор с сопротивлением R и индуктивную катушку с индуктивностью L. При t ≥ 0 уравнение, описывающее электрическую цепь, будет иметь вид:

. (7.12)

Характеристическое уравнение цепи

Имеет два корня

(7.13)

При решении 7.12 возможны при случае (в зависимости от вида корней характеристического уравнения):

а) , – переходный процесс в цепи имеет апериодический характер. Напряжение на конденсаторе в переходном режиме

(7.14)

б) , – предельный случай апериодического процесса. Напряжение на конденсаторе в переходном режиме

(7.15)

в) , – переходный процесс в цепи имеет колебательный характер. Напряжение на конденсаторе в переходном режиме

, (7.16)

где – угловая частота колебаний.

5) Короткое замыкание цепи R – L – C. Пусть заряженный до напряжения U конденсатор в момент времени t = 0 подключает к цепи с последовательно соединенными резистором и индуктивной катушкой (рис. 7.4).

Рисунок 7.4 – Схема короткого замыкания цепи R – L – C

Переходный процесс будет соответствовать разряду конденсатора на резистор и индуктивную катушку. Электрическая цепь (рис. 7.4) в переходном режиме характеризуется уравнением

. (7.17)

Решение уравнения (7.17) будет иметь вид:

а) апериодический разряд конденсатора (корни отрицательные, вещественные и разные):

(7.18)

б) предельный случай апериодического разряда (корни отрицательные, вещественные и равные):

(7.19)

в) колебательный разряд конденсатора (корни комплексно-сопряженные):

(7.20)

6) Визуальное наблюдение на экране электронного осциллографа переходного процесса в электрической цепи осуществляется путем периодического повторения наблюдаемого процесса с соответствующей частотой и его записью во времени на экране. Для осуществления такого периодического повторения питание электрической цепи осуществляется прямоугольными импульсами с частотой f = 50 Гц и длительностью равной половине периода, т.е. t_п = 0,01 с.

7) При исследовании цепи R – C заряд и разряд конденсатора будет происходить 50 раз в секунду. При этом необходимо обеспечить практическое завершение переходного процесса заряд – разряд в течении ∆t = t_п = 0,01 с. Исходя из указанного условия при известной емкости (при известном сопротивлении), предварительно нужно рассчитать сопротивление (емкость) так, чтобы изменение напряжения U_C(t) от нуля до 0,99U₀ (U₀ – амплитуда прямоугольного импульса) при его зарядке, или от U₀ до 0,01U₀ – при разрядке осуществлялось за время не больше 0,01 с. для этого необходимо, чтобы τ = RC = 0,002 с.

8) Исследование цепи R – L осуществляется повторным включением и коротким замыканием ее с частотой 50 Гц. Это обеспечивает длительное наблюдение переходного процесса. Значение с обеспечивает выбор сопротивления в цепи катушки.

9) В цепи R – L – C могут иметь место:

а) апериодический;

б) предельный случай апериодического;

в) колебательные переходного процесса.

Чтобы иметь возможность наблюдать периодический процесс в цепи, необходимо определить сопротивление контура из условия 10L/R ≤ 0,01 с. При выборе дополнительного сопротивления R_д = R – R_к необходимо знать сопротивление катушки R_к.