
- •2.10.3 Задание
- •1. Изучить зависимость эдс индукции от числа витков во вторичной цепи.
- •2.Изучить зависимость эдс индукции от частоты переменного тока.
- •3. Проверить независимость коэффициента взаимной индукции от частоты генератора.
- •4. Проверить независимость коэффициента взаимной индукции от силы тока, создающего магнитное поле.
- •2.10.4 Контрольные вопросы
- •Литература:
- •Рабочая формула
Министерство образования Республики Беларусь
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНФОРМАТИКИ И РАДИОЭЛЕКТРОНИКИ

Кафедра физики
ЛАБОРАТОРНАЯ РАБОТА
№ 2.10
ИЗУЧЕНИЕ ЯВЛЕНИЯ
ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
МЕТОДИЧЕСКОЕ ПОСОБИЕ
Минск 2011
ЛАБОРАТОРНАЯ РАБОТА № 2.10
ИЗУЧЕНИЕ ЯВЛЕНИЯ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
2.10.1 ЦЕЛЬ РАБОТЫ
Экспериментально изучить частные случаи основного закона электромагнитной индукции.
2.10.2 КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Явление электромагнитной индукции состоит в том, что при изменении магнитного потока через поверхность, ограниченную контуром, в последнем возбуждается электродвижущая сила индукции. Если проводящий контур замкнутый, то под действием этой ЭДС в нем возникает электрический ток, называемый индукционным. Согласно закону Ленца, индукционный ток всегда имеет такое направление, что его магнитное поле противодействует изменению магнитного потока.
Магнитный поток Ф сквозь поверхность, ограниченную произвольным замкнутым контуром, может изменяться по ряду причин: за счет изменения геометрии контура, изменения его расположения в магнитном поле, вследствие зависимости магнитной индукции от времени. Согласно закону Фарадея, электродвижущая сила индукции, возникающая в контуре, численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную этим контуром:
![]() . (2.10.1)
. (2.10.1)
Уравнение (2.10.1) выражает основной закон электромагнитной индукции в общем виде.
Рассмотрим контур, состоящий из N витков, в котором индуцируется ЭДС. Поскольку витки соединяются последовательно, ЭДС, возбуждаемые в отдельных витках, будут складываться. Поэтому
![]() .
.
Величину
![]() называют
потокосцеплением или полным магнитным
потоком. Если потоки Фi,
пронизывающие каждый из витков,
одинаковы, то
называют
потокосцеплением или полным магнитным
потоком. Если потоки Фi,
пронизывающие каждый из витков,
одинаковы, то
![]() .
Отсюда
.
Отсюда
![]() .
(2.10.2)
.
(2.10.2)
Хотя величина ЭДС
индукции не зависит от способа изменения
магнитного потока, однако механизм ее
возникновения при этом оказывается
разным. Обратимся сначала к случаю,
когда поток изменяется вследствие
движения проводящего контура (или
изменения его геометрии) в постоянном
магнитном поле. Здесь роль сторонних
сил, разделяющих разноименные заряды
в проводнике, играет магнитная составляющая
силы Лоренца
![]()
![]() .
.
Если неподвижный
проводник находится в изменяющемся со
временем магнитном поле, то механизм
возникновения ЭДС оказывается другим.
Изменяющееся магнитное поле
![]() возбуждает вихревое электрическое
поле
возбуждает вихревое электрическое
поле
![]() ,
под действием которого носители заряда
приходят в движение. Таким образом, в
неподвижном контуре возникает ЭДС
индукции
,
под действием которого носители заряда
приходят в движение. Таким образом, в
неподвижном контуре возникает ЭДС
индукции
![]() .
.
Собственное
магнитное поле проводника с током I
создает полный поток
![]() через поверхность, ограниченную этим
проводником. Согласно закону
Био-Савара-Лапласа, индукция поля B
пропорциональна току I.
Значит, величины
и I
тоже пропорциональны друг другу, т.е.
через поверхность, ограниченную этим
проводником. Согласно закону
Био-Савара-Лапласа, индукция поля B
пропорциональна току I.
Значит, величины
и I
тоже пропорциональны друг другу, т.е.
![]() , (2.10.3)
, (2.10.3)
где L индуктивность проводника. Величина L зависит от геометрии контура (т.е. от его формы и размеров), а также от магнитных свойств среды, в которой он находится, характеризуемых проницаемостью . Однако если среда ферромагнитная, то является сложной функцией от тока. Значит, индуктивность проводника оказывается зависящей от величины тока. Формула (2.10.3) остается справедливой и для такого случая.
Если ток в контуре
изменяется каким-либо образом, то это
приводит к изменению собственного
потока
.
В результате в контуре возбуждается
ЭДС, называемая электродвижущей силой
самоиндукции
![]() .
Из выражений (2.10.2)
и
(2.10.3)
следует, что
.
Из выражений (2.10.2)
и
(2.10.3)
следует, что
![]() .
.
Если среда неферромагнитная и контур не деформируется, то L = const и
![]() .
.
Под действием ЭДС самоиндукции возникает индукционный ток, который по закону Ленца противодействует изменению тока в цепи: замедляет его возрастание или убывание.
Рассмотрим два контура, расположенных близко друг к другу (рис.2.10.1).

При прохождении
электрического тока I1
по контуру 1 в каждой точке пространства
создается магнитное поле. Индукция
этого поля пропорциональна току I1.
Поэтому магнитный поток через поверхность,
ограниченную контуром
2, также пропорционален I1:
![]() ,
где коэффициент пропорциональности
L21
называется коэффициентом взаимной
индукции. При изменении тока I1
меняется также магнитный поток 21
и в контуре 2
индуцируется
ЭДС:
,
где коэффициент пропорциональности
L21
называется коэффициентом взаимной
индукции. При изменении тока I1
меняется также магнитный поток 21
и в контуре 2
индуцируется
ЭДС:
![]() .
.
Аналогично при
протекании в контуре
2 тока I2
создается магнитное поле и поверхность,
ограниченную контуром 1, пронизывает
магнитный поток
![]() .
При изменении тока I2
индуцируется ЭДС в контуре
1:
.
При изменении тока I2
индуцируется ЭДС в контуре
1:
![]() .
.
Говорят, что между этими контурами существует магнитная связь, само же явление возникновения ЭДС в одном из проводников вследствие изменения тока в другом называют взаимной индукцией. Коэффициенты L12 и L21 называются коэффициентами взаимной индукции. Их величина зависит от формы, размеров и взаимного расположения проводников, а также от магнитной проницаемости среды. В отсутствие ферромагнетиков L12 = L21. На явлении взаимной индукции основано действие трансформаторов.
В работе предлагается проверить на опыте некоторые частные случаи явления электромагнитной индукции. Схема установки приведена на рис. 2.10.2. Изменяющееся магнитное поле в длинном соленоиде L0 возбуждает вихревое электрическое поле, под действием которого носители заряда в катушках L1 L5 приходят в движение.
Таким образом, в этих катушках возникает ЭДС индукции, амплитудное значение которой измеряется осциллографом (ЭО) (рис.2.10.2.). Кнопочный переключатель (П) дает возможность подключить одну из секций L1 L5 (число витков в каждой секции катушки одинаково).

![]()

 П
П


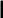



 L1
L2
L3
L4
L5
L1
L2
L3
L4
L5



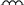



![]() L0
L0


![]()
![]()
Согласно закону электромагнитной индукции
![]() ,
,
где 2 ЭДС индукции, возникающая во вторичной катушке; Ф21 магнитный поток пронизывающий вторичную катушку; I1 – ток, текущий в первичной катушке и создающий магнитное поле.
Так как в катушке L0 течет переменный ток I1, изменяющийся по закону
![]() ,
то
,
то
![]() .
.
Амплитудное значение тока во вторичной цепи
![]() ,
,
где R сопротивление вторичной цепи.
Следовательно,
 , (2.10.4)
, (2.10.4)
где
![]()
ЭДС, определяемая с помощью осциллографа.
ЭДС, определяемая с помощью осциллографа.
Переключатель П2 дает возможность катушкам меняться ролями (рис. 2.10.3). Звуковой генератор (ЗГ) подключается к одной из катушек L1 L5, а осциллограф (ЭО) к соленоиду L0. При этом коэффициент взаимной индукции находят по формуле
 . (2.10.5)
. (2.10.5)
Рассчитав коэффициент взаимной индукции, легко убедиться в справедливости формулы
![]() . (2.10.6)
. (2.10.6)
 L1-L5
L1-L5
П2
L0
2.10.3 Задание
1. Изучить зависимость эдс индукции от числа витков во вторичной цепи.
Установить
на макете переключатели П1 в положение
"ПРЯМО" и П2 в положение "ГЕНЕРАТОР".
Увеличивая число секций вторичной
катушки, поочередно переключая кнопки
L1
– L5
, измерить величину ЭДС индукции
осциллографом. Установить частоту
генератора 4000 Гц, а ток, проходящий через
соленоид
L0
(ручка Рег. выхода генератора), поддерживать
постоянным (20 мА). Величину ЭДС индукции
определить по формуле
![]() ,
где ly
амплитуда сигнала на экране осциллографа
в больших делениях шкалы, y
чувствительность осциллографа ("в/дел.")
указана на передней панели осциллографа.
Результаты измерений и вычислений
занести в табл. 2.10.1.
,
где ly
амплитуда сигнала на экране осциллографа
в больших делениях шкалы, y
чувствительность осциллографа ("в/дел.")
указана на передней панели осциллографа.
Результаты измерений и вычислений
занести в табл. 2.10.1.
Таблица 2.10.1
К, число секций |
ly, дел |
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
|
|
Построить график
зависимости
![]() .
.
Измерить ЭДС индукции во вторичной катушке L5 при включении ее в противоположном направлении ( П1 в положении “ОБРАТНО”). Проанализировать результат.
2.Изучить зависимость эдс индукции от частоты переменного тока.
Установить П2 в положение "ГЕНЕРАТОР". Изменяя частоту генератора (от 2000 Гц до 20000 Гц, с шагом 2000 Гц), определить ЭДС индукции на одной из секций (L3) вторичной катушки. Силу тока поддерживать постоянной (10 мА). Результаты измерений и вычислений записать в табл. 2.10.2.
Таблица 2.10.2
№ |
f, Гц |
ly, дел |
, В |
1. |
|
|
|
2. |
|
|
|
… |
|
|
|
Построить график
зависимости
![]() .
.
3. Проверить независимость коэффициента взаимной индукции от частоты генератора.
Подать сигнал с генератора на соленоид L0 (П2 в положении “ГЕНЕРАТОР”), нажать кнопку L3 вторичной катушки и определить амплитуду ЭДС индукции с помощью осциллографа. Миллиамперметром контролировать ток (10 мА) через соленоид L0. Используя формулу (2.10.4) определить L21 для трех частот (8000 гц 10000 гц 12000 гц). Затем переключатель П2 перевести в положение "ОСЦИЛЛОГРАФ" и снять такие же показания ЭДС индукции на соленоиде L0, необходимые для вычисления L12 по формуле (2.10.5). Миллиамперметром контролировать ток через катушку L3 (20мА). Результаты измерений и вычислений записать в табл. 2.10.3.
Таблица 2.10.3
№ |
f Гц |
I1 = 10, mA |
I2 = 20, mA |
L21/L12 |
||
, В |
L21, Гн |
|
L12, Гн |
|||
1. |
8000 |
|
|
|
|
|
2. |
10000 |
|
|
|
|
|
3. |
12000 |
|
|
|
|
|
