Распределение молекул по скоростям

Полученное выражение (5) для функции распределения молекул газа по z-компонентам скоростей не может быть «привилегией» именно этой скорости. Такие же выражения должны определять и распределения молекул по другим компонентам скоростей, так что

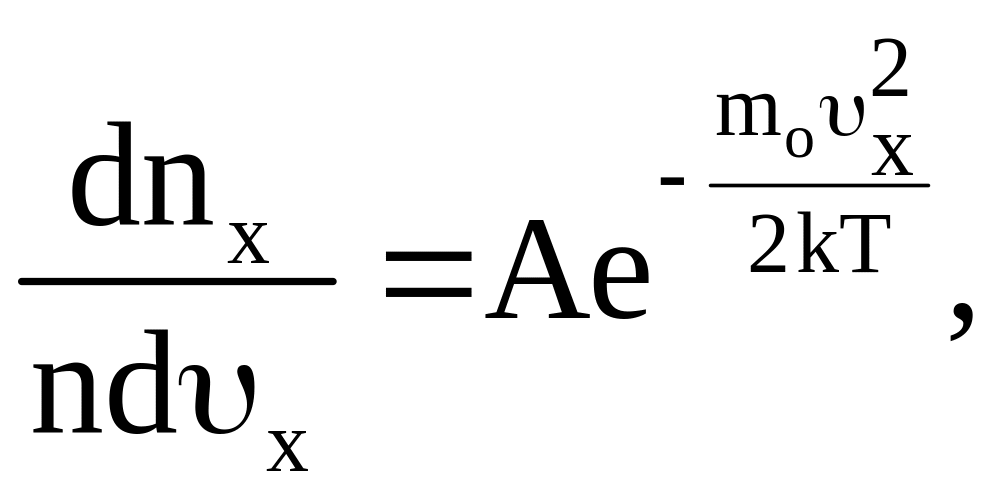
Теперь можно найти вероятность того, что скорость молекулы удовлетворяет одновременно трем условиям:

1. ее составляющая по оси X лежит в пределах от υ_х до υ_х + dυ_х.

2. составляющая по оси У лежит в пределах oт υ_у до υ_у + dυ_у.

3. составляющая по оси Z лежит в пределах от υ_г до υ_z + dυ_z.

Значения составляющих скорости по каждой из осей координат не зависят от значений составляющих по другим осям. Поэтому вероятность того, что скорость молекулы одновременно удовлетворяет трем указанным условиям, есть вероятность сложного события. Она равна произведению вероятностей каждого из событий в отдельности. Если обозначить через dn_xуz число молекул в единице объема газа, составляющие которых по осям координат лежат в пределах, указанных выше, то можно записать:

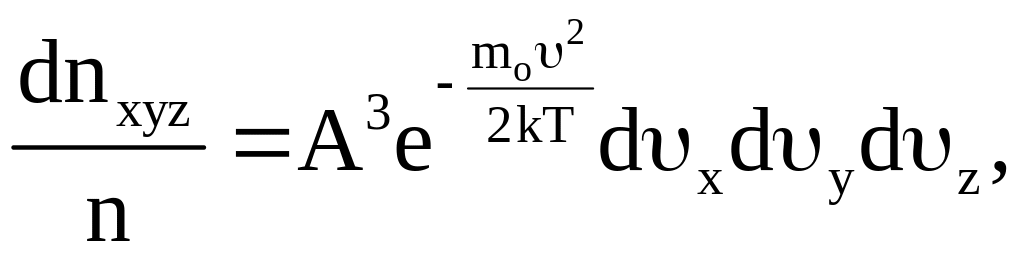(9)

где Учитывая (7), выражение (9) можно переписать в виде

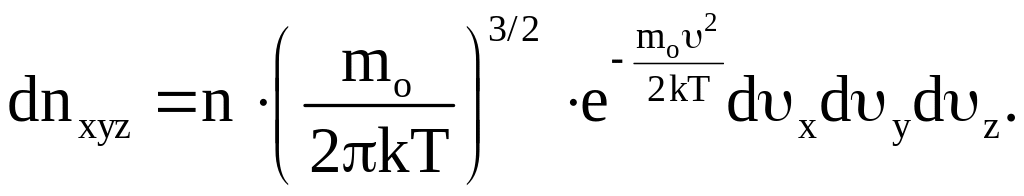(10)

Эта формула показывает, сколько молекул, из числа находящихся в единице объема газа, обладают скоростями, составляющие которых по осям координат лежат в интервалах между υ_х и υ_х + dυ_х, υ_у и υ_у + dυ_у, υ_г до υ_z + dυ_z. То есть обладают скоростью, лежащей в интервале, заданном и по величине, и по направлению. Этой формуле можно дать наглядное геометрическое толкование. Представим себе, что собрали все молекулы единицы объема газа, компоненты скорости υ которых заключены в указанных выше интервалах, и выпустили их. Через 1 секунду все они окажутся на расстоянии υ от начального положения в параллелепипеде со сторонами dυ_х, dυ_у и dυ_z, т. е. в объеме dV = dυ_х dυ_у dυ_z. Это показано на рис. 3, на котором этот мысленный опыт представлен в своеобразной системе координат, по осям которой отложены составляющие υ_х, υ_у и υ_z. Число молекул, отнесенное к единице объема этого параллелепипеда (не путать с числом молекул в единице объема газа; здесь идет речь о единице объема в «пространстве» скоростей), согласно (10) равно

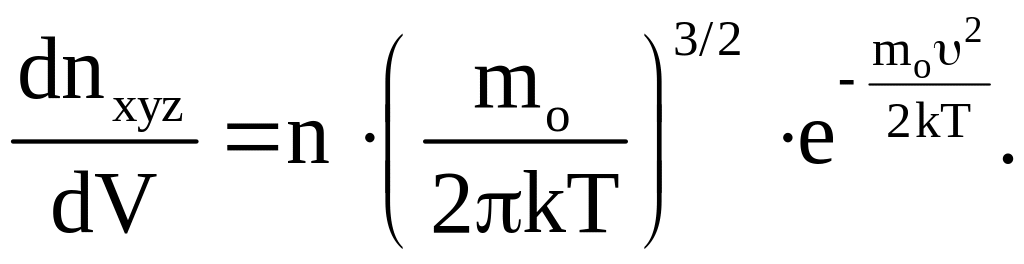(11)

Рис. 3. Пространство скоростей	Рис. 4. Шаровой слой толщиной dυ и радиусом υ

Величина эта не может, конечно, зависеть от направления вектора скорости υ. Поэтому нетрудно теперь найти и функцию распределения молекул по скоростям независимо от их направления. Действительно, если собрать вместе все молекулы единицы объема газа, скорости которых заключены в интервале от υ до υ +dυ по всем направлениям, и выпустить их, то они, разлетаясь по всем направлениям, через 1 секунду окажутся равномерно распределенными в шаровом слое толщиной dυ и радиусом υ (рис. 4). Этот шаровой слой складывается из тех «параллелепипедов», о которых говорилось выше. Число молекул в единице объема этого слоя (его, опять-таки, нельзя путать с числом молекул в единице объема газа) такое же, как и в каждом параллелепипеде, т. е. определяется формулой (10). Число же молекул во всем слое – это и есть число молекул в единице объема газа, скорости которых лежат в интервале от υ до υ +dυ. Число это равно:

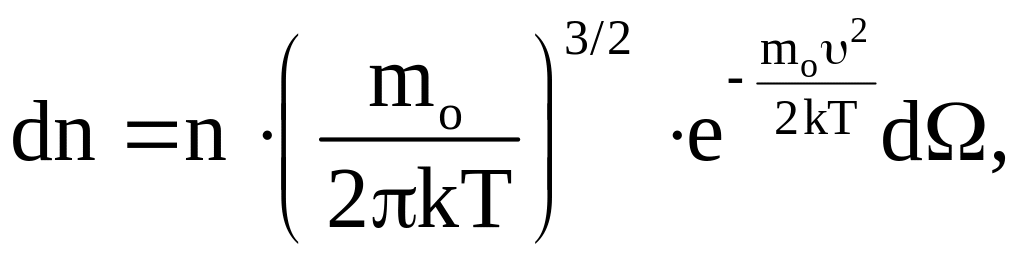
где d – объем шарового слоя, равный 4υ²dυ. Таким образом,

или

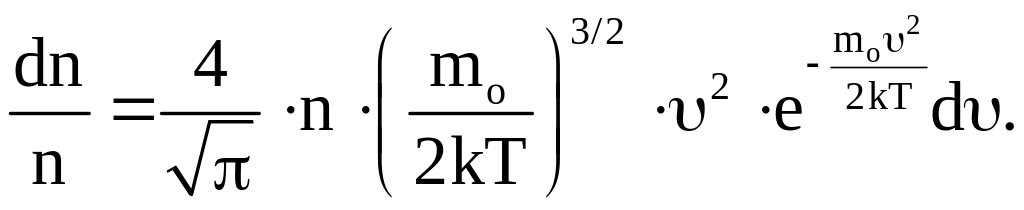(12)

Формула (12) выражает закон Максвелла распределения молекул по скоростям.

Величина dn/n это вероятность того, что у произвольно выбранной молекулы газа скорость окажется лежащей в интервале между υ до υ +dυ. Иными словами, dn/n это доля всех молекул единицы объема, скорости которых лежат в интервале от υ до υ +dυ.

Величина

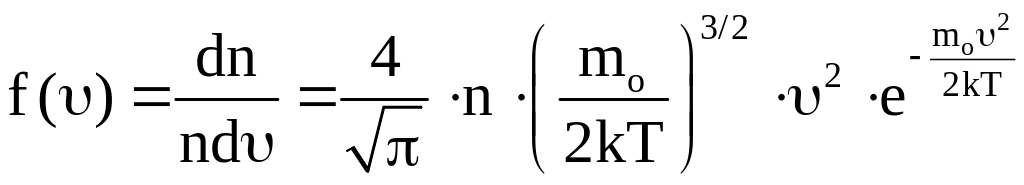(13)

представляет собой функцию распределения молекул по скоростям. Она определяет долю молекул единицы объема газа, скорости которых заключены в интервале скоростей, равном единице, включающем данную скорость.