Распределение Максвелла – равновесное распределение

При выводе распределения молекул по скоростям (Приложение 1) не принимались во внимание столкновения между молекулами, хотя они не могут не влиять на скорости молекул, а значит и на распределение их по скоростям. В действительности именно благодаря столкновениям и устанавливается максвелловское распределение по скоростям. Представим, что газ находится в таком состоянии, что все молекулы имеют одинаковые (по модулю) скорости. Такое состояние не может быть устойчивым (равновесным), потому что столкновения между молекулами непременно приведут к тому, что скорости молекул перестанут быть одинаковыми. При каждом столкновении двух молекул скорость одной из них увеличивается, а скорость другой уменьшается.

Дж. Максвелл впервые обратил внимание на то, что должно существовать такое состояние, при котором число молекул, скорость которых при столкновениях увеличивается, будет равно числу молекул, у которых скорость в результате столкновений уменьшается. Такое состояние и является равновесным. Это состояние, при котором параметры системы (P, V, T) сохраняют определенное значение сколь угодно долго при неизменных внешних условиях. Именно такому состоянию и соответствует максвелловское распределение по скоростям.

Позже Людвиг Больцман показал, что если газ находится в состоянии, в котором его молекулы распределены по скоростям не по Максвеллу, то такой газ, благодаря столкновениям молекул, сам собой переходит в состояние с максвелловским распределением. Распределение Максвелла (иногда говорят: распределение Максвелла – Больцмана) – это равновесное распределение. При неравновесном состоянии газа распределение в нем молекул по скоростям будет отличаться от максвелловского.

Молекулярные движения, происходящие в газе, называют хаотическими. Можно дать следующее определение понятию хаотичности тепловых движений: движение молекул полностью беспорядочно (хаотично), если скорости молекул распределены по закону Максвелла.

Такие вполне хаотические движения молекулы совершают, когда газ находится в состоянии равновесия. Это состояние характеризуется величиной температуры, которая в свою очередь определяет среднюю кинетическую энергию движения молекул. Отсюда следует, что температура определяет среднюю кинетическую энергию именно хаотических движений. Всякое же направленное движение молекул, каковы бы ни были их скорости в таком движении, никакого отношения к температуре не имеет.

Практическая часть Идея метода

Для изучения закона распределения молекул газа по скоростям используется механическая модель газа. На рис. 4 приведена схема установки для моделирования распределения Максвелла. Роль молекул играют шарики, определенное количество которых засыпается во внутреннее пространство прибора 1. Шарики приводятся в движение из-за колебательного движения основания 11 и абсолютно упруго сталкиваются друг с другом и со стенками сосуда. Так имитируется тепловое движение молекул.

Интенсивность «теплового» движения можно изменять, меняя напряжение, подаваемое на прибор от источника (2). Величина подаваемого напряжения U и высота H поршня (6) (рабочие параметры) влияют на движение шариков, моделируя различную интенсивность теплового движения. За движением шариков можно наблюдать через боковые стеклянные стенки устройства (1).

Если регулятор (7) переместить вверх, то выходное отверстие прибора будет открыто и шарики, вылетая из отверстия кюветы, попадут в верхний приемник (4), разделенный на 24 отсека. Верхний приемник жестко крепится на нижнем приемнике (3), отсеки которого имеют цилиндрическую форму и совпадают с отсеками верхнего приемника. Каждый верхний отсек заполняется шариками, имеющими вполне определенное значение горизонтальной скорости. Все шарики, попавшие в отсеки верхнего приемника, осыпаются через отверстия в дне в отдельные отсеки нижнего приемника с прозрачными стенками. Полученное в результате этого распределение шариков по отсекам нижнего приемника подобно распределению Максвелла для скоростей молекул газа.

При получении распределения с выбранными рабочими параметрами количество шариков в приборе будет непрерывно уменьшаться, поэтому необходимо периодически пополнять количество шариков. Для того чтобы определить необходимое количество шариков и интервал времени, через который это нужно делать, необходимо провести подготовительную работу. Для этого в наборе кювет есть кюветы-накопители (рис.5 а). Они имеют глухую прозрачную стенку (не видна на рис. 5а) и круглое отверстие посередине или вверху выпуклой части. Эту кювету помещают выпуклой частью внутрь на выходное отверстие прибора (рис. 4). В этом случае, если открыть регулятор 7, то шарики, вылетая из выходного отверстия, прибора попадут в кювету-накопитель, а не в верхний приемник шариков. Так можно определить количество вылетевших шариков и время заполнения кюветы при заданных рабочих параметрах.

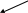
Рис. 4. Экспериментальная установка.

1 – прибор для имитации теплового движения;

2 – источник питания; 3 – нижний приемник шариков;

4 – верхний приемник шариков; 5 – место крепления кюветы на выходном отверстии; 6 – поршень; 7 – регулятор, открывающий выходное отверстие; 8 – рукоятка для перемещения поршня по высоте; 9 – регулировочный винт для перемещения поршня по высоте; 10 – отверстие для засыпания шариков; 11 – основание внутренней камеры прибора, которое совершает колебательные движения, приводя шарики в движение; 12 – весы; 13 – крышка с отверстием для извлечения шариков из отсеков приемника.

а

дополнительное

отверстие

) б)

Р

дополнительное

отверстие

ис. 5. Кюветы с отверстием посередине выпуклой части:

а) кювета-накопитель для подготовки эксперимента;

б) кювета для получения распределения с дополнительным отверстием в нижней части

Для выполнения части работы, связанной непосредственно с моделированием распределения Максвелла в наборе кювет есть кюветы, имеющие узкое отверстие на прозрачной стенке (не видно на рис. 5б) и два круглых отверстия на выпуклой части (посередине или вверху выпуклой части и дополнительное – внизу). Если открыть регулятор (7), то шарики, вылетая из выходного отверстия, через круглое отверстие на выпуклой части попадут из прибора (1) в кювету, затем, вылетев с горизонтальной скоростью через узкое направляющее отверстие кюветы, попадут в отсеки верхнего приемника (4). Нижнее отверстие меньшего диаметра служит для того, чтобы шарики, вылетевшие из прибора, но имеющие недостаточную скорость, высыпались обратно во внутреннюю камеру прибора.

Число шариков N₁, попавших в первый отсек, эквивалентно числу молекул, скорости которых имеют значения от 0 до υ₁. Число шариков N₂, попавших во второй отсек, эквивалентно числу молекул со скоростями от υ₁ до υ₂ и т. д. Обозначим общее число шариков (молекул) N. Отношение N_i / N есть вероятность того, что молекулы модельного газа имеют скорости в интервале υ_i ÷ υ_i + υ.

крышка-фиксатор кюветы кювета

Рис.6. Крупный план места крепления кюветы на устройстве (1)

Экспериментальные результаты (количество шаров с разной скоростью) можно в соответствии с (3) представить в виде графика функции:

(12)

где F_Э – плотность вероятности в условиях эксперимента, υ – изменение скорости, соответствующее изменению пути на s, определяемое как

Δυ = υ_i+1 – υ_i, (13)

s – длина ячейки верхнего приемника.

В случае движения тела под действием силы тяжести горизонтальная составляющая его скорости остается постоянной. Если шарик вылетает из отверстия установки горизонтально, то скорость шарика, попавшего в i-й отсек можно найти, зная его дальность полета s_i:

(14)

где s_i – это расстояние по горизонтали от отверстия кюветы до соответствующего отсека верхнего приемника шариков, определяемое как s_i = s ^. i; где i – номер отсека приемника (i = 1, …24).

В вертикальном направлении шарик, вылетает из отверстия установки горизонтально, движется равноускоренно. Время движения шарика по вертикали можно найти, зная высоту h, с которой он падает как

(15)

где g – ускорение свободного падения на поверхности Земли, h – разница высот между отверстием кюветы и основанием верхнего приемника шариков.

Подставив (14) в (13), получим

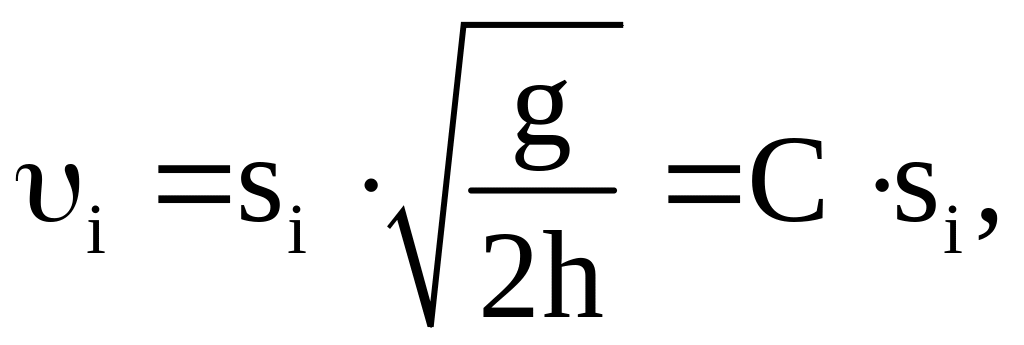(16)

где С – постоянная в условиях одного эксперимента величина, определяемая как

Зная общее количество шариков N в отсеках, количество шариков в каждом отсеке N_i и среднее значение скорости для данного отсека υ_i*, можно найти среднюю арифметическую скорость

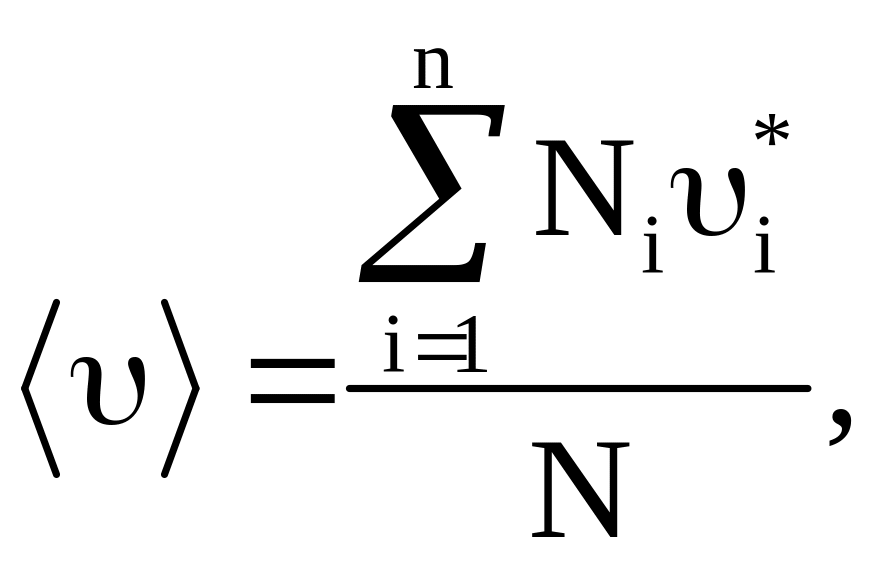(17)

где n – число заполненных отсеков.

Среднюю квадратическую скорость можно найти как

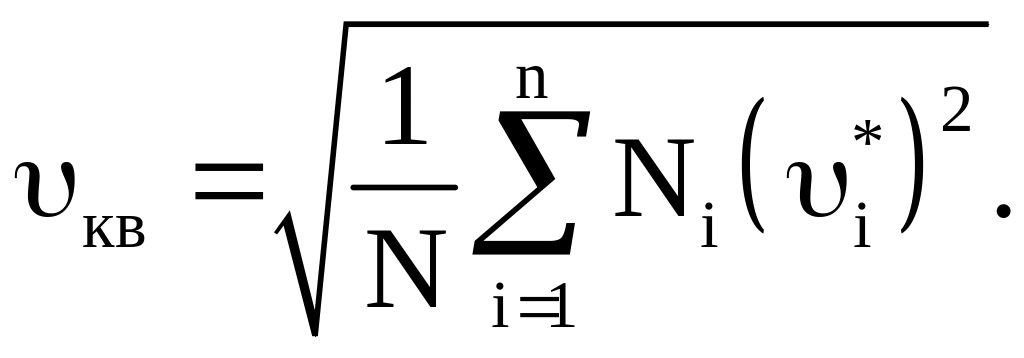(18)

Максимум кривой распределения Максвелла соответствует наиболее вероятной скорости υ_в, определяемой по соотношению (7). Зная характерные скорости распределения, можно проверить справедливость соотношения (11), устанавливающего связь между ними. Закон распределения Максвелла (5), учитывая выражение (7) для υ_в, можно представить как

. (19)

Таким образом, зная значение наиболее вероятной скорости, можно рассчитать теоретическое распределение Максвелла F(υ) и сравнить его с полученным экспериментально F_Э(υ).

Упражнение 1. Подготовка эксперимента

1. Соберите установку в соответствии с рис. 4.

2. Определите среднюю массу одного стеклянного шара m_о путем взвешивания известного числа шаров (например, 50).

3. Подняв крышку-фиксатор, на выходном отверстии закрепите кювету-накопитель (рис. 5, 6) выпуклой частью внутрь. Проверьте, чтобы круглые выходные отверстия на самом приборе и кювете были точно отцентрированы. При необходимости дополнительно зафиксируйте положение кюветы скотчем.

4. Поршень (7) с помощью регулировочного винта (8) (рис. 4) установите на высоте H = 6-8 см.

5. Заполните прибор 1 шариками так, чтобы они образовали слой высотой не более, чем 3-4 шарика (что составляет примерно 3 мм). Точное количество шариков подбирается экспериментально. Общее количество шариков в приборе должно быть таким, чтобы при включении напряжения они могли двигаться и распределяться по всему объему внутренней камеры между основанием 11 и поршнем 6 (рис. 4). Для каждого рабочего напряжения необходимо тщательно подбирать нужное количество шариков, производя пробное включение напряжения. Напряжение U (рабочее напряжение) задается на источнике 2 поворотом ручки регулировки напряжения. Значение U выберите в диапазоне 10-12 В. Установите значение силы тока 2А.

Примечание: Шарики засыпайте медленно и следите, чтобы они не застревали.

6. После заполнения прибора (1) шариками определите время  заполнения кюветы-накопителя и массу М (или количество) шариков, вылетевших из выходного отверстия и скапливающихся в кювете за это время для заданных рабочих параметров (U, H). Для этого подождите, пока все шарики придут в движение. Затем, перемещая регулятор (7) вверх, откройте выходное отверстие, включите секундомер и зафиксируйте время заполнения кюветы. После завершения измерений уменьшите напряжение на источнике до нуля и закройте выходное отверстие, перемещая регулятор (7) вниз.

7. Аккуратно снимите кювету-накопитель с выходного отверстия, пересыпьте шарики в емкость с заранее определенной массой. Определите массу М и количество вылетевших шаров N* = М/m_о, которые попали в кювету-накопитель.

Примечание: Во время выполнения упражнения 2 в прибор нужно будет подсыпать шарики в количестве равном примерно N*/3 (или М/3) с интервалом времени   3, чтобы сохранять среднюю плотность частиц во внутренней камере устройства (1) при движении шариков.

8. Подготовьте требуемые для подсыпания в ходе эксперимента шарики, поместив их в пробирки или мерные стаканчики.

У пражнение 2. Получение распределения Максвелла для модели идеального газа.

1. На выходном отверстии закрепите кювету для получения распределения (рис. 5, 6) выпуклой частью внутрь. Проверьте, чтобы круглые выходные отверстия на самом приборе и кювете были отцентрированы. От этого зависит результат эксперимента! При необходимости дополнительно зафиксируйте положение кюветы скотчем.

2. Досыпьте в устройство (1) шарики, вылетевшие оттуда в кювету-накопитель при выполнении п. 6 подготовительного эксперимента.

3. Установите напряжение, при котором вы выполняли Упражнение 1. Подождите, пока все шарики придут в движение, затем, перемещая регулятор 7 вверх, откройте выходное отверстие, включите секундомер. В течение 10 - 20 минут наблюдайте за заполнением отсеков нижнего приемника. Не забывайте во время эксперимента подсыпать в прибор шарики с интервалом времени  в количестве, определенном при выполнении Упражнения 1.

4. По окончании эксперимента выключите секундомер и уменьшите напряжение на источнике до нуля. Закройте выходное отверстие, перемещая регулятор 7 вниз.

5. С помощью кисточки очистите ячейки верхнего приемника от оставшихся там шариков. Аккуратно снимите верхний приемник.

Упражнение 3. Расчет характерных скоростей для экспериментально полученного распределения.

1. Измерьте высоту столбиков Y_i во всех отсеках нижнего приемника и занесите в таблицу результаты измерений.

2. Определите массу шариков m в каждом из отсеков. Для этого необходимо закрепить специальную крышку с отверстием на нижнем приемнике и, осторожно перемещая ее по длине приемника, последовательно совмещать отверстие в крышке с каждой из 24 ячеек нижнего приемника. Шарики из каждого отсека поместите в емкости для взвешивания и взвесьте.

3. Рассчитайте число N_i шариков в каждом отсеке. Результаты занесите в таблицу.

4. Запишите измеренную с помощью штангенциркуля длину ячейки верхнего приемника – расстояние s.

5. С помощью штангенциркуля измерьте расстояние h – разницу высот между выходным отверстием прибора и приемным устройством.

6. По формуле (16) рассчитайте скорости шариков υ_i для всех отсеков приемника. Результаты измерений занесите в таблицу.

7. Найдите υ по (13). (Нужно ли это делать для всех отсеков?)

8. Рассчитайте среднее значение скорости υ_i* для каждого интервала скоростей по формуле:

υ_i* = υ_i + υ/2.

9. По формуле (12) рассчитайте плотность вероятности для каждого отсека.

10. Постройте график зависимости F_Э(υ), он будет отображать экспериментально полученное распределение.

11. По графику зависимости F_Э(υ) определите наиболее вероятную скорость υ_в для распределения, полученного экспериментально.

12. По формуле (17) вычислите среднюю арифметическую скорость для данных эксперимента. В качестве значения скорости для каждого отсека используйте значение υ_i*.

13. По формуле (18) вычислите среднеквадратичную скорость. В качестве значения скорости для каждого отсека используйте значение υ_i*.

14. Проверьте, выполняется ли соотношение (11) между среднеквадратичной и средней арифметической скоростью. Для этого найдите частное этих величин по данным вычислений пп. 12, 13. Сделайте вывод.

15. Используя соотношение (11), найдите наиболее вероятную скорость υ_в, используя для этого, значение средней арифметической скорости. Повторите вычисления υ_в, используя теперь значение среднеквадратичной скорости.

16. Усредните результаты вычислений наиболее вероятной скорости υ_в, полученные в пп. 11, 15.

17. По среднему значению наиболее вероятной скорости, по формуле (19) рассчитайте теоретический вид распределения Максвелла. Для этого рассчитайте значение функции F_i (υ_i*) для середины каждого интервала скоростей.

18. По результатам расчетов п. 17 постройте график, отражающий теоретический вид распределения Максвелла. Рекомендуется этот график построить в тех же осях, что и экспериментальное распределение. Сравните представленные на графике экспериментальные данные и теоретическое распределение и сделайте вывод.

Таблица 2.

Таблица для записи результатов измерений.

Рабочие параметры U = В, H = см
i	Yi, см	mi,г	Ni	si, м	i м/с	i* м/с		Ni . i*	( i*)2(м/с)2	Ni .( i*)2	Fi( i*)
1
2
….
24

Упражнение 4*. Изучение влияния рабочих параметров установки на вид распределения Максвелла.

1. Для получения нового распределения выполните подготовительные работы, предусмотренные пп.2-3 Упражнения 1.

2. Задайте другие рабочие параметры, изменив или высоту поршня, или значение напряжения на единицу.

3. Следуя указаниям пп.5-6 определите время заполнения кюветы и массу М шариков, вылетающих из выходного отверстия при новых параметрах.

4. Затем выполните задания упражнений 2,3.

5. Сравните распределения, полученные при различных параметрах.

Упражнения, отмеченные *, выполняются студентами физичесrих специальностей.