
Приложение б
Информационный материал практической направленности
Действия над матрицами: |
1
|
2
|
|
3
|
|
Вычисление определителя: |
1
|
2
«
+ – |
|
3
|
|
Обратная матрица: |
|
Матричные уравнения: |
1
|
2
|
|
Формулы Крамера: |
|
Метод Гаусса |
Прямой ход
С помощью элементарных преобразований
расширенная матрица системы
Обратный ход Осуществляется переход к системе и выполняется поиск неизвестных |
Пример выполнения заданий
Задание 1. Выполнить действия над
матрицами
![]() ,
где
,
где
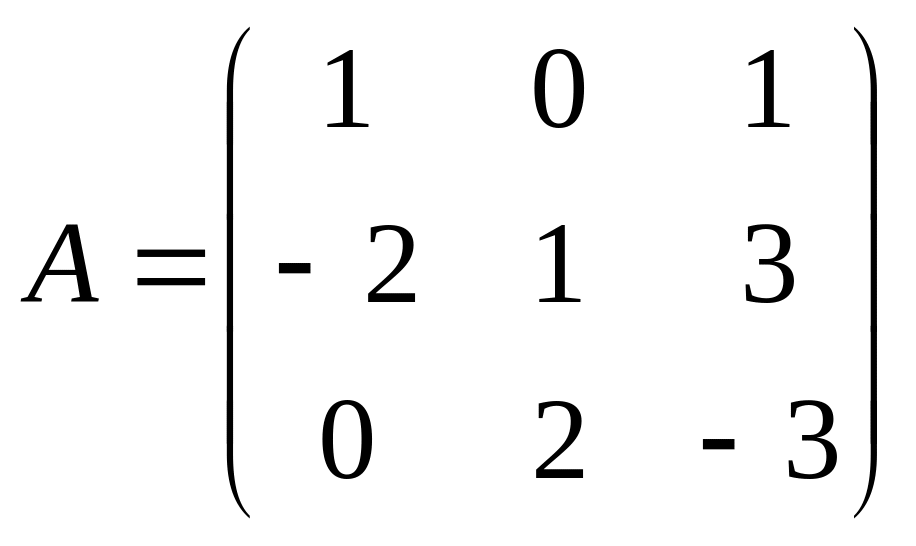 и
и
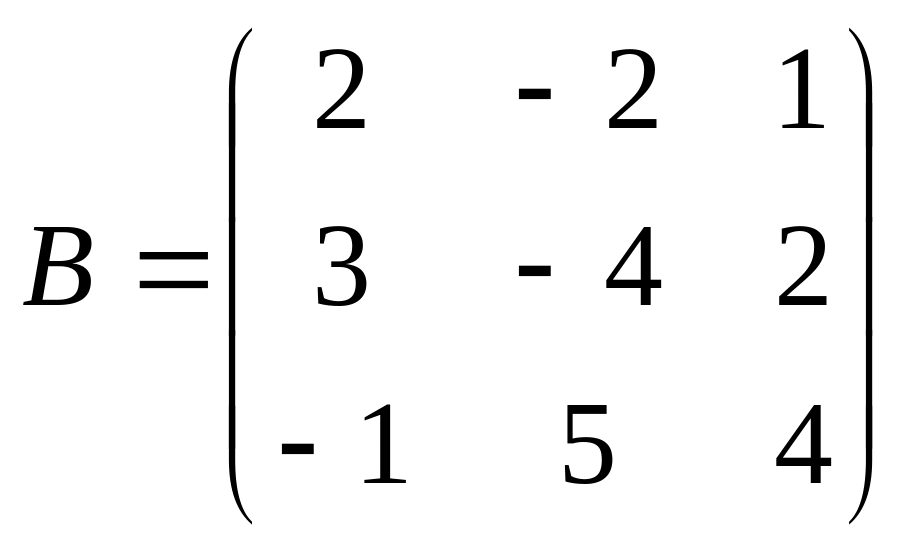 .
.
Решение:
1 Вычислим
![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Получили
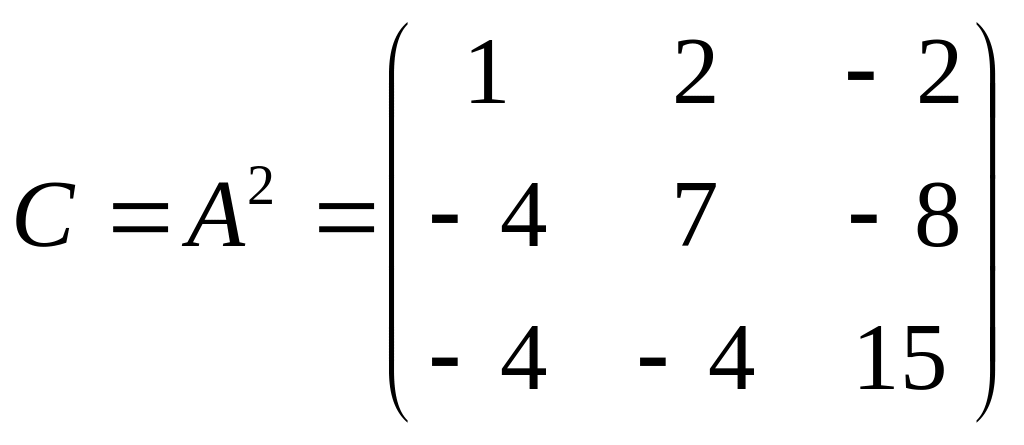 .
.
2 Вычислим
![]() :
:
 .
.
3 Вычислим
![]() :
:
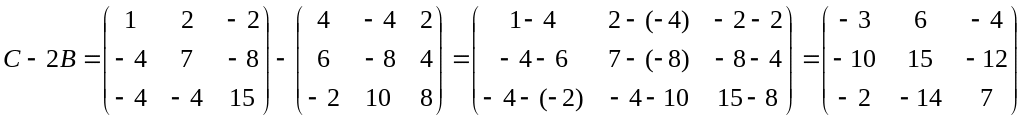 .
.
Ответ:
 .
.
Задание 2. Вычислить определитель
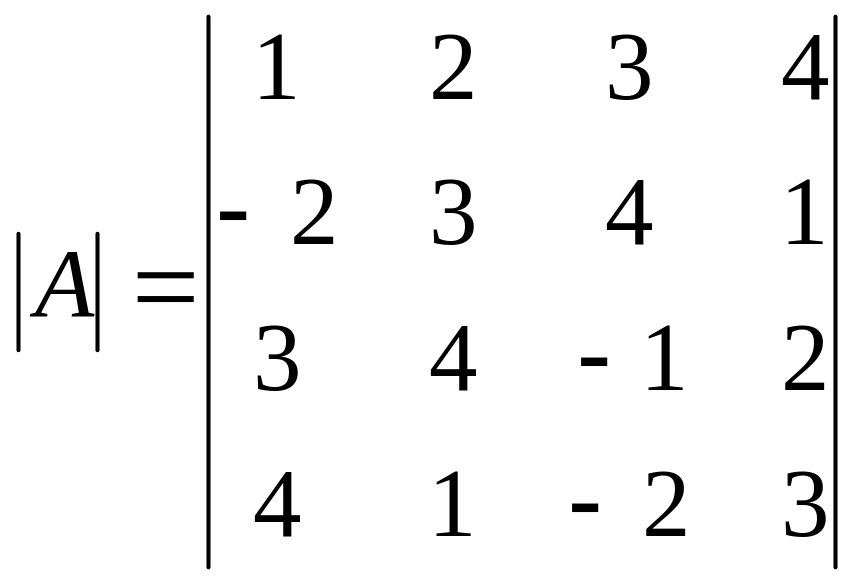 .
.
Решение:
Выполним элементарные преобразования
определителя для того, чтобы получить
нули для элементов
![]() и
и
![]() .
.
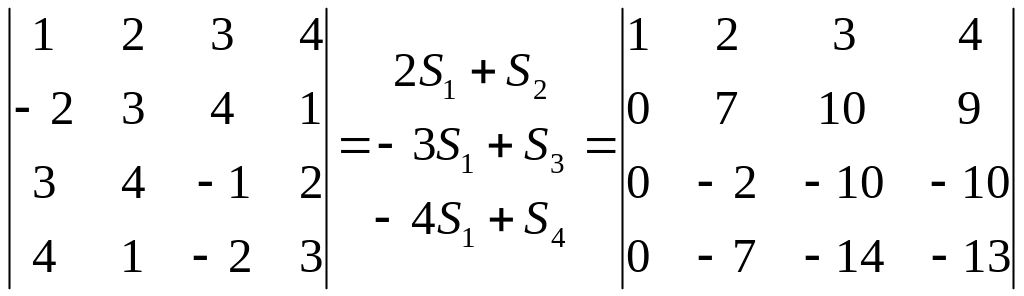 ,
где Si
–соответствующая строка определителя.
,
где Si
–соответствующая строка определителя.
Запишем разложение по первому столбцу.
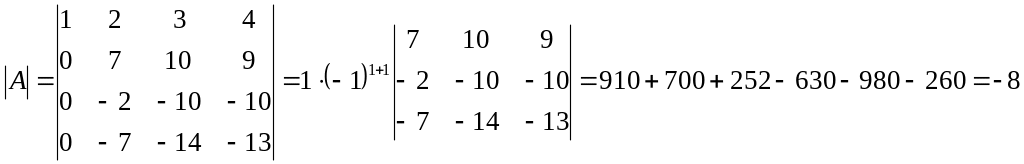 .
.
Определитель третьего порядка вычислен по правилу «Треугольника».
Задание № 3. Решить систему уравнений
![]() методом Крамера и с помощью обратной
матрицы.
методом Крамера и с помощью обратной
матрицы.
Решение:
1 Метод Крамера
Вычислим определитель матрицы системы:
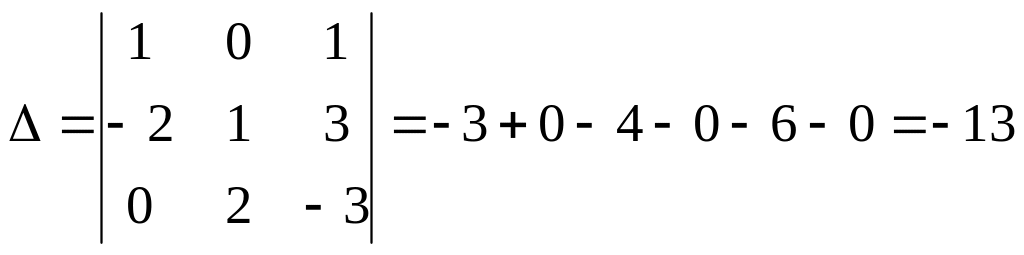 .
.
Составим и вычислим дополнительные определители путем замены соответствующего столбца определителя матрицы системы на столбец свободных членов:
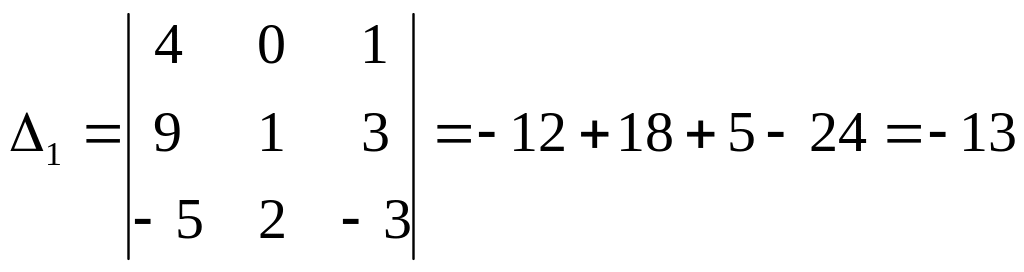 ;
; 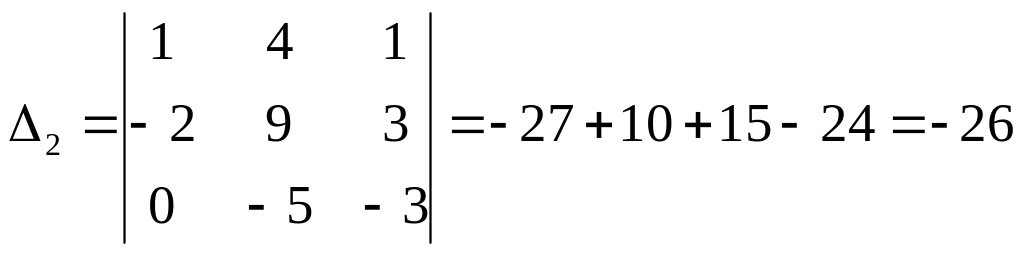 ;
;
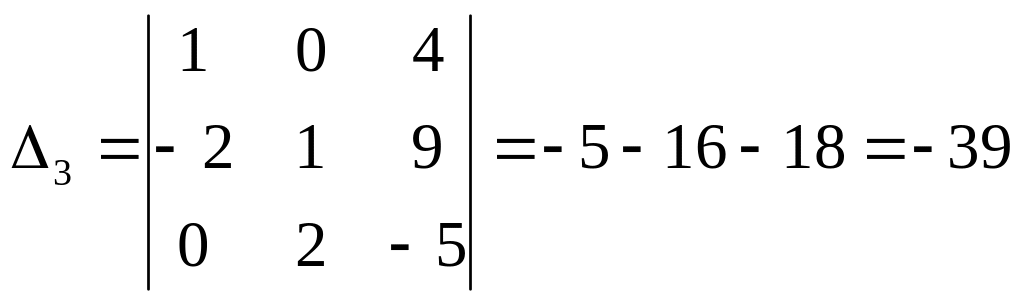 .
.
![]() ;
; ![]() ;
; ![]() .
.
Ответ:
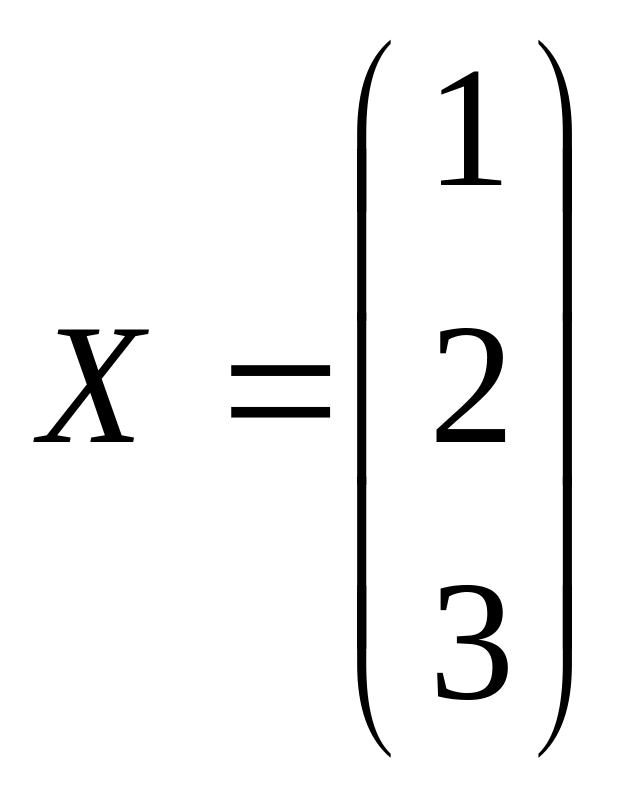 .
.
2 С помощью обратной матрицы:
![]()
Вычислим обратную матрицу;
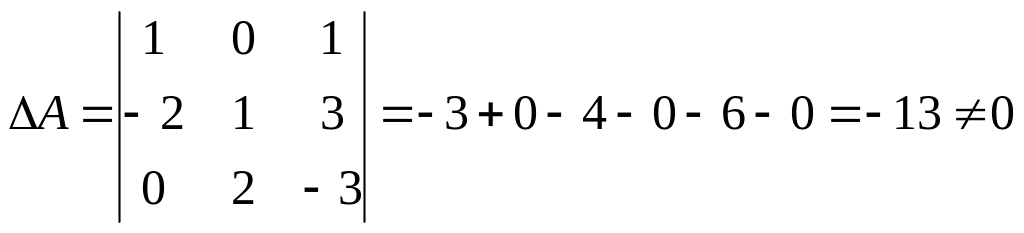 ;
;
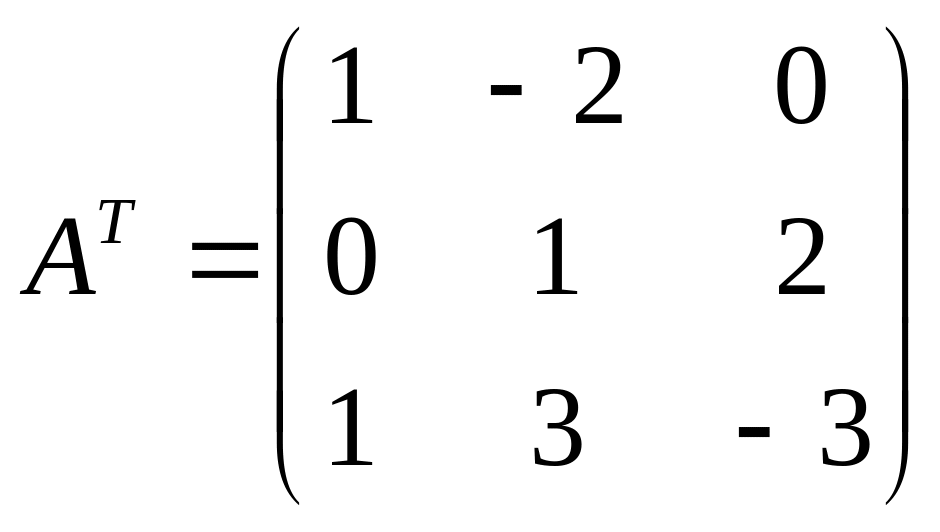 ;
;
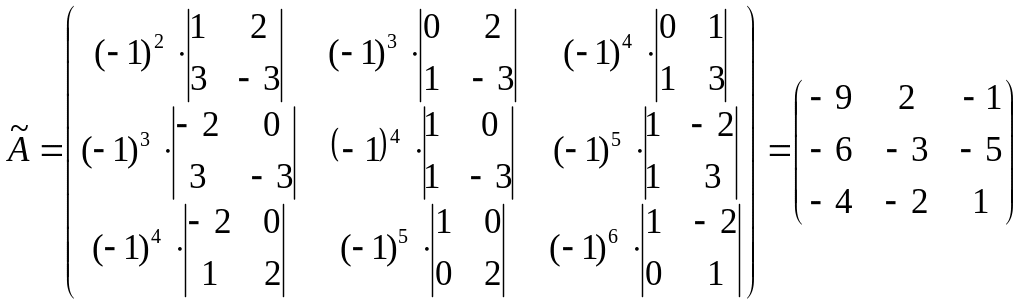 ;
;
 .
.
Вычислим матрицу Х:
![]() ;
;
![]() ;
;
![]() .
.
Ответ: .
Задание 4. Решить систему уравнений
![]() методом Гаусса.
методом Гаусса.
Решение:
Прямой ход
Составим расширенную матрицу системы:
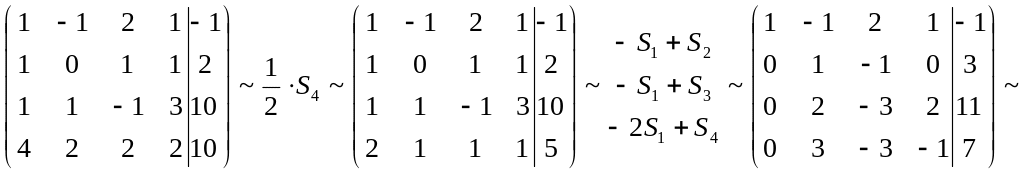
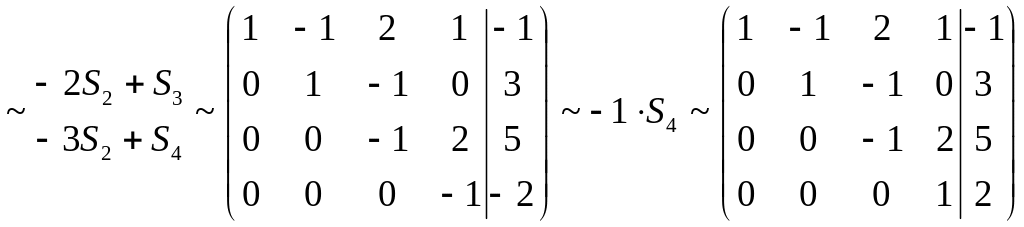 .
.
Si – номер соответствующей строки расширенной матрицы
Обратный ход
Составим систему уравнений:
![]()
Ответ:
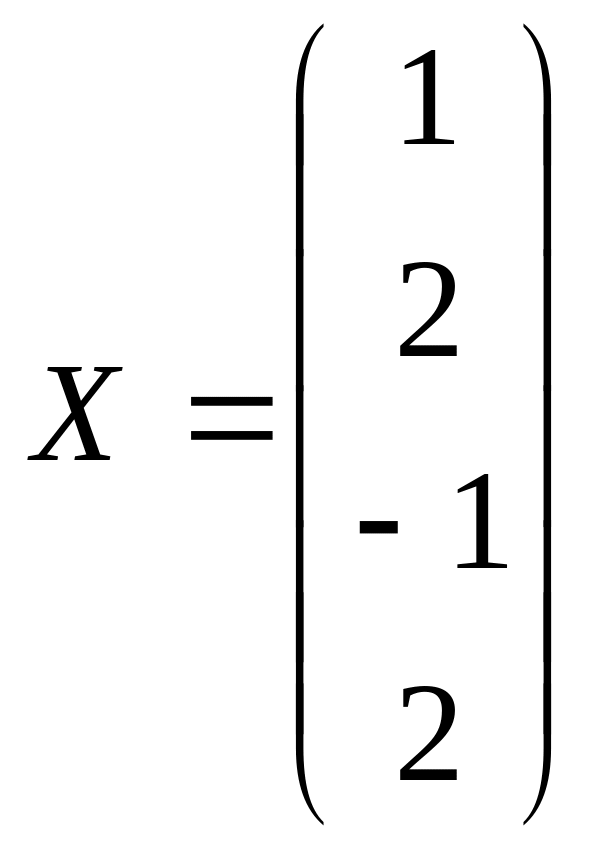

 Правило
треугольника»
Правило
треугольника»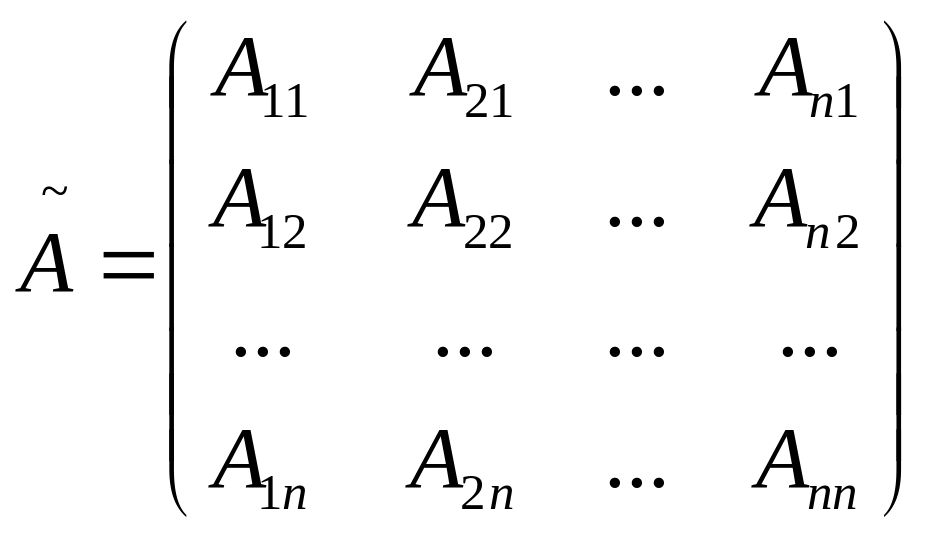 ,
,
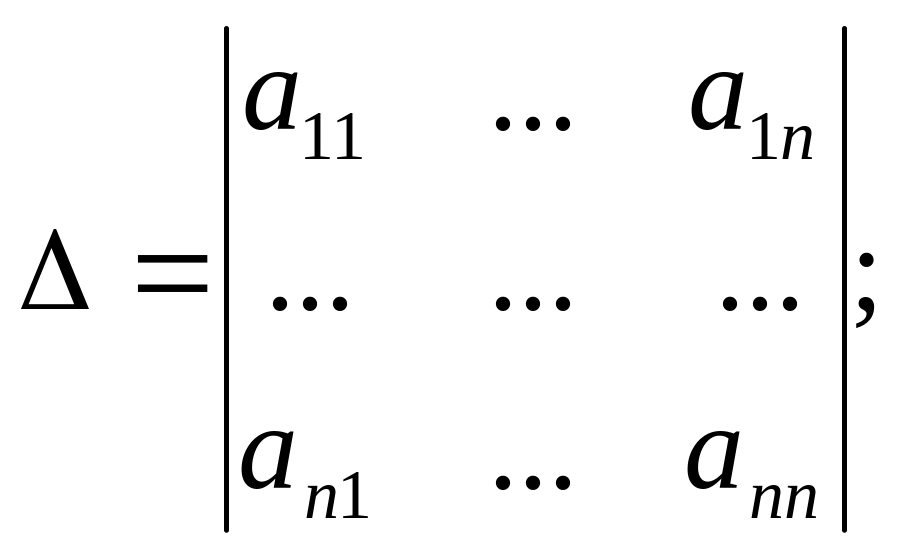
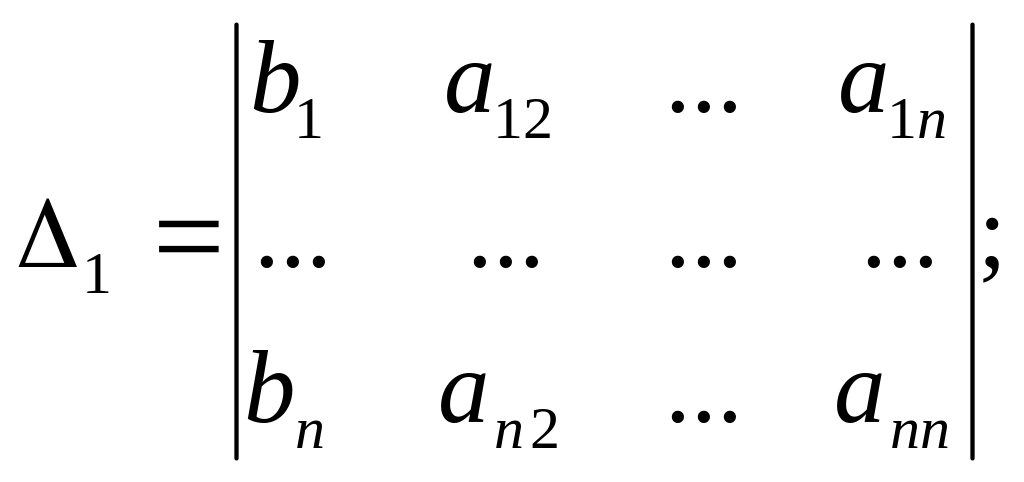
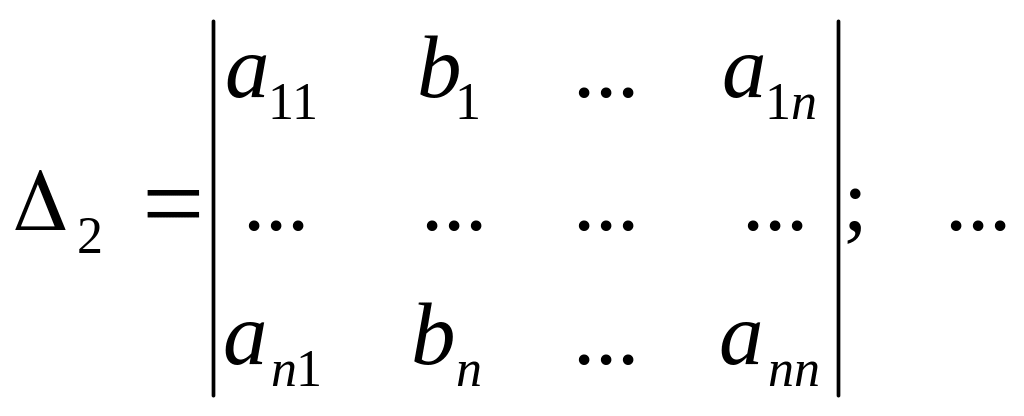
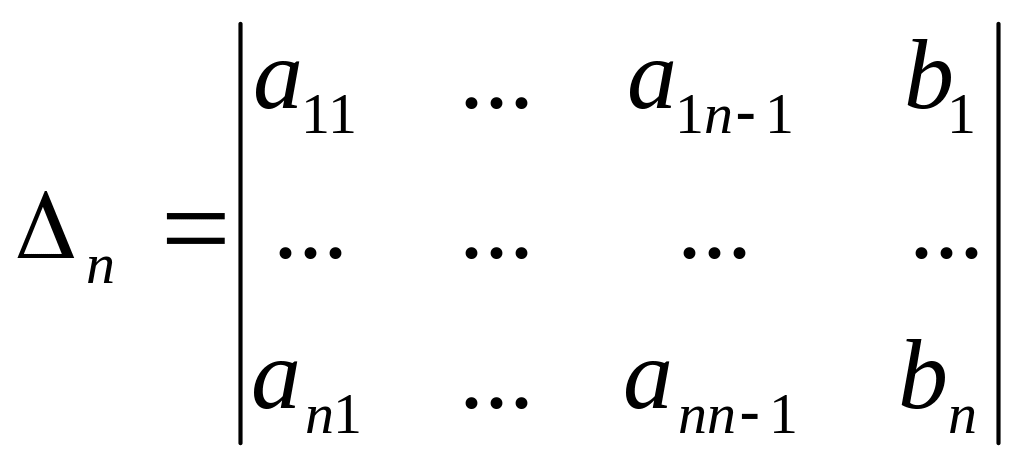
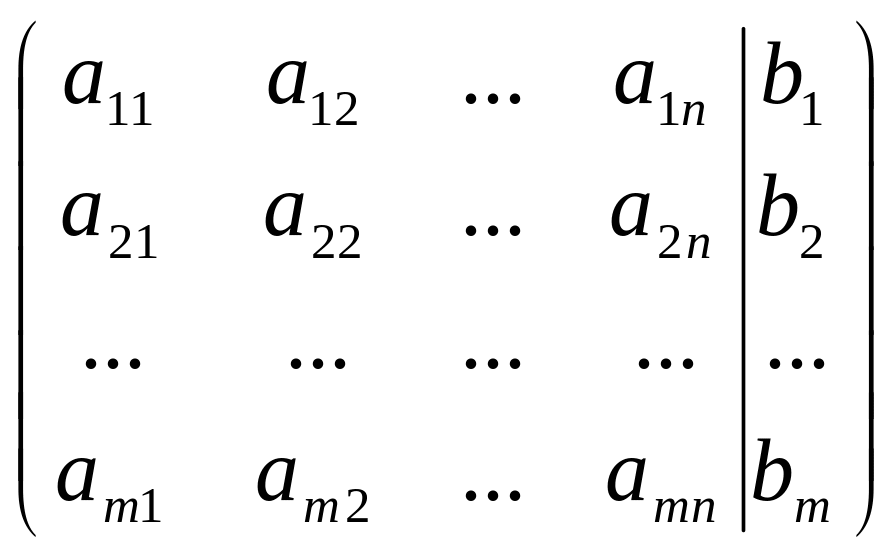 приводится к виду
приводится к виду
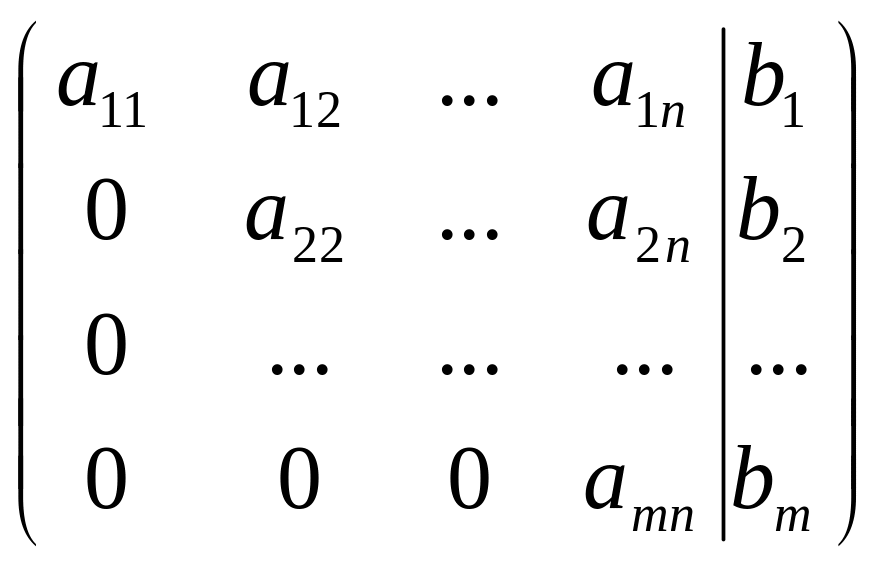 .
.