
- •7. Элементы теории статистического синтеза оптимальных радиотехнических устройств
- •7.1. Классификация задач оптимальных методов радиоприема
- •7.2. Апостериорная плотность вероятности
- •7.3. Линейная фильтрация
- •7.4. Линейная оптимальная фильтрация по критерию максимума отношения сигнал/шум
- •7.5. Оптимальная фильтрация стационарных случайных сигналов
- •7.6. Фильтрация Калмана
- •Методические указания
- •Список литературы
7.4. Линейная оптимальная фильтрация по критерию максимума отношения сигнал/шум
Если линейный фильтр в соответствии с заданным критерием обрабатывает аддитивную смесь сигнала и шума наилучшим образом, то такой линейный фильтр называется оптимальным. В этом подразделе рассмотрим оптимальную линейную фильтрацию сигналов известной формы. Такая ситуация характерна для радиолокации, где принятый сигнал является точной масштабной копией переданного сигнала.
Пусть на вход линейного стационарного
фильтра с импульсной характеристикой
![]() воздействует сумма полезного сигнала
и шума. На выходе линейного фильтра
полезный сигнал создает отклик
воздействует сумма полезного сигнала
и шума. На выходе линейного фильтра
полезный сигнал создает отклик
![]()
Попытаемся отыскать такую импульсную
характеристику
,
чтобы величина![]() ,
определяемая значением отклика фильтра
в точке
,
определяемая значением отклика фильтра
в точке
![]() ,
достигала максимально возможного
значения. Фильтр с такой импульсной
характеристикой называется согласованным
с заданным входным сигналом или кратко
согласованным фильтром.
,
достигала максимально возможного
значения. Фильтр с такой импульсной
характеристикой называется согласованным
с заданным входным сигналом или кратко
согласованным фильтром.
Таким образом, необходимо отыскать
такую импульсную характеристику
,
чтобы отклик на выходе в момент времени
![]()
![]() (7.8)
(7.8)
достигал максимально возможного значения по модулю. Применим к правой части выражения (7.8) известное неравенство Шварца-Буняковского в интегральной форме:
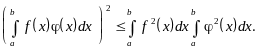
Получим:
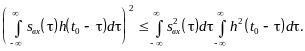 (7.9)
(7.9)
Знак равенства в выражении (7.9) достигается в том случае, когда подынтегральные функции пропорциональны друг другу, т.е.
![]() (7.10)
(7.10)
где
![]() -
произвольный числовой коэффициент.
Тогда, используя в выражении (7.10) замену
переменной
-
произвольный числовой коэффициент.
Тогда, используя в выражении (7.10) замену
переменной
![]() ,
получаем, что модуль правой части
выражения (7.8) достигнет максимума при
,
получаем, что модуль правой части
выражения (7.8) достигнет максимума при
![]()
Рис.
7.1. Импульсная характеристика фильтра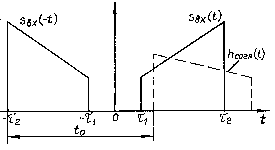
Как видно из рис 7.1, чтобы импульсная
характеристика
![]() удовлетворяла условию физической
реализуемости, т.е.
=0
при t<0, необходимо, чтобы выполнялось
неравенство
удовлетворяла условию физической
реализуемости, т.е.
=0
при t<0, необходимо, чтобы выполнялось
неравенство
![]()
Применяя преобразование Фурье к обеим частям соотношения (7.10), находим частотный коэффициент передачи согласованного фильтра
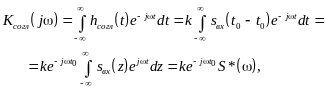 (7.11)
(7.11)
где
![]() спектральная плотность, комплексно
сопряженная со спектральной плотностью
спектральная плотность, комплексно
сопряженная со спектральной плотностью
![]() входного сигнала
входного сигнала
![]() .
.
Таким образом, частотный коэффициент
передачи согласованного фильтра
выражается через спектральную плотность
полезного сигнала
,
для выделения которого из шума и
предназначен фильтр. В формуле (7.11)
коэффициент k
определяет уровень усиления фильтра,
а множитель
![]() определяет смещение отклика фильтра
по оси времени на время
определяет смещение отклика фильтра
по оси времени на время
![]() .
.
Особенностью согласованного фильтра является то, что при формировании отклика на своем выходе им используется как информация об амплитудно-частотном спектре входного сигнала, так и его фазово-частотный спектр. Фильтр с малым ослаблением должен пропускать лишь гармонические компоненты, частоты которых расположены в области, где спектральная плотность полезного сигнала отличается от нуля. Кроме того, фильтр выполняет коррекцию фазовых сдвигов гармонических составляющих входного сигнала таким образом, что в момент все эти гармонические составляющие складываются на выходе когерентно, имея одни и те же фазовые сдвиги. Тем самым отклик на выходе фильтра в момент достигает максимально возможного уровня
![]() (7.12)
(7.12)
где
![]() энергия полезного выделяемого сигнала
энергия полезного выделяемого сигнала
![]() .
.
Из выражения (7.12) следует, что максимальное значение отклика согласованного фильтра не зависит от формы сигнала, а определяется его энергией.
Найдем отношение сигнал/шум на выходе фильтра, определяемое как отношение пикового значения мощности выходного сигнала в момент к средней мощности выходного шума:
Для определенности положим, что шум
![]() представляет собой стационарный белый
гауссов шум с равномерным спектром
мощности уровня
представляет собой стационарный белый
гауссов шум с равномерным спектром
мощности уровня
![]() на всей числовой оси. В этом случае
дисперсия шума на выходе
на всей числовой оси. В этом случае
дисперсия шума на выходе

Тогда, учитывая полученный результат и формулу (7.12), находим:
Рис. 7.2. Прямоугольный
видеоимпульс и напряжения на выходе
отдельных элементов согласованного
фильтра
Перейдем теперь к вопросам синтеза согласованных фильтров. Для этого рассмотрим конкретный пример построения согласованного филь-тра для прямоугольного видеоимпульса (рис. 7.2).
Положим, что импульс возникает в момент
времени
![]() ,
имеет длительность
,
имеет длительность
![]() и амплитуду А. Найдем спектральную
плотность такого сигнала:
и амплитуду А. Найдем спектральную
плотность такого сигнала:
 (7.13)
(7.13)
Найдем частотный коэффициент передачи
фильтра
![]() в предположении, что на его выходе
максимум отклика достигает в момент
в предположении, что на его выходе
максимум отклика достигает в момент![]() , т.е.
, т.е.
![]() .
В соответствии с формулой (7.11) и с учетом
(7.13), находим:
.
В соответствии с формулой (7.11) и с учетом
(7.13), находим:
 (7.14)
(7.14)
Рис. 7.3. Согласованный
фильтр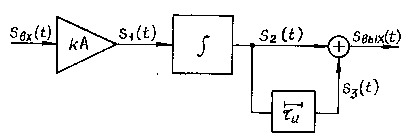
![]() ,
интегратора, которому в частной области
соответствует умножение на
,
интегратора, которому в частной области
соответствует умножение на
![]() (см. формулу (7.14)), линии задержки на время
и вычитающего устройства. На вычитающее
устройство в соответствии с формулой
(7.14) подается напряжение по двум каналам:
непосредственно с интегратора и через
линию задержки. На выходе согласованного
фильтра получаем сигнал треугольной
формы высотой
(см. формулу (7.14)), линии задержки на время
и вычитающего устройства. На вычитающее
устройство в соответствии с формулой
(7.14) подается напряжение по двум каналам:
непосредственно с интегратора и через
линию задержки. На выходе согласованного
фильтра получаем сигнал треугольной
формы высотой
![]() и длительностью
и длительностью![]() :
:
![]()
где энергия прямоугольного видеоимпульса
![]() .
.
Для некоторых простых по форме сигналов с небольшой базой удается добиться приемлемых результатов при их линейной фильтрации более простыми в конструктивном исполнении фильтрами по сравнению с оптимальными. Такие фильтры называют квазиоптимальными, т.е. фильтрами, близкими по характеристикам к оптимальным.
Рассмотрим простую интегрирующую
RC-цепочку
с импульсной характеристикой
![]() где
где
![]() - постоянная времени цепи. Пусть на вход
такой цепи воздействует сумма полезного
сигнала в виде прямоугольного видеоимпульса
(см. рис. 7.2) и гауссов белый шум со
спектральной плотностью мощности
.
В этом случае отклик на воздействие
полезного сигнала достигает максимума
при
- постоянная времени цепи. Пусть на вход
такой цепи воздействует сумма полезного
сигнала в виде прямоугольного видеоимпульса
(см. рис. 7.2) и гауссов белый шум со
спектральной плотностью мощности
.
В этом случае отклик на воздействие
полезного сигнала достигает максимума
при
![]() .
Таким образом, используя формулу (7.8)
при
.
Таким образом, используя формулу (7.8)
при![]() ,
находим:
,
находим:
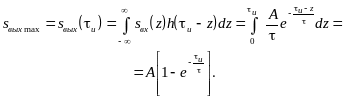
Частотный коэффициент передачи
интегрирующей RC-цепи
![]() .
.
Поэтому, с учетом формулы (7.7), дисперсия шума на выходе будет:
![]()
Отсюда максимальное значение отношения сигнал/шум на выходе RC-цепи:
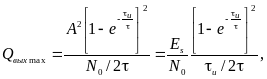 (7.15)
(7.15)
где в последнем равенстве учтено, что
![]() -
энергия прямоугольного видеоимпульса.
-
энергия прямоугольного видеоимпульса.
Как следует из предыдущих результатов,
первый сомножитель правой части
соотношение (7.15) равен максимальному
отношению сигнал/шум на выходе
согласованного фильтра, а второй
сомножитель
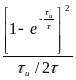 характеризует проигрыш в отношении
сигнал/шум интегрирующей RC-цепи по
сравнению с согласованным фильтром,
приведенным на рис. 7.3. Второй сомножитель
достигает максимума при
характеризует проигрыш в отношении
сигнал/шум интегрирующей RC-цепи по
сравнению с согласованным фильтром,
приведенным на рис. 7.3. Второй сомножитель
достигает максимума при
![]() ,
равного 0,814. Таким образом, при
соответствующем выборе постоянной
времени RC-цепи получим, что интегрирующая
RC-цепь при фильтрации прямоугольного
видеоимпульса на фоне шума проигрывает
в эффективности (в смысле отношения
сигнал/шум на выходе) всего лишь на 18,6
%. Именно RC-цепь с такими характеристиками
и будет квазиоптимальным согласованным
фильтром для прямоугольного видеоимпульса.
,
равного 0,814. Таким образом, при
соответствующем выборе постоянной
времени RC-цепи получим, что интегрирующая
RC-цепь при фильтрации прямоугольного
видеоимпульса на фоне шума проигрывает
в эффективности (в смысле отношения
сигнал/шум на выходе) всего лишь на 18,6
%. Именно RC-цепь с такими характеристиками
и будет квазиоптимальным согласованным
фильтром для прямоугольного видеоимпульса.
