Программирование на Pascal / Delphi / Лекции по Паскалю / Алгоритмы вычисления некоторых математических функций

Алгоритмы вычисления некоторых математических функций

Некоторые математические функции, такие как синус, косинус, натуральный логарифм, экспонента вычисляются в ЭВМ как суммы убывающих последовательностей чисел (суммы рядов).

Общая математическая модель таких задач следующая

где ,

Метод решения

Так как постановке задачи вычисляется бесконечная сумма, то прямой подход – суммирование всех элементов не является приемлемым алгоритмом (нарушается свойство конечности алгоритма – алгоритм должен выполняться за конечное число шагов). Исходя из того, что последовательность чисел убывающая, то «маленькие» числа в сумму можно не включать. Поэтому пока значение очередного числа, входящего в сумму больше заданной точности (малого числа е), это число добавляется к сумме.

Если для вычисления очередного числа входящего в сумму требуется некоторый алгоритм, то пытаются свести вычисление очередного числа к рекуррентной формуле. Для этого последовательность чисел, входящих в сумму представляют как геометрическую прогрессию. Предварительно (до разработки алгоритма) вычисляют первое число, входящее в сумму и выводят формулу знаменателя геометрической прогрессии

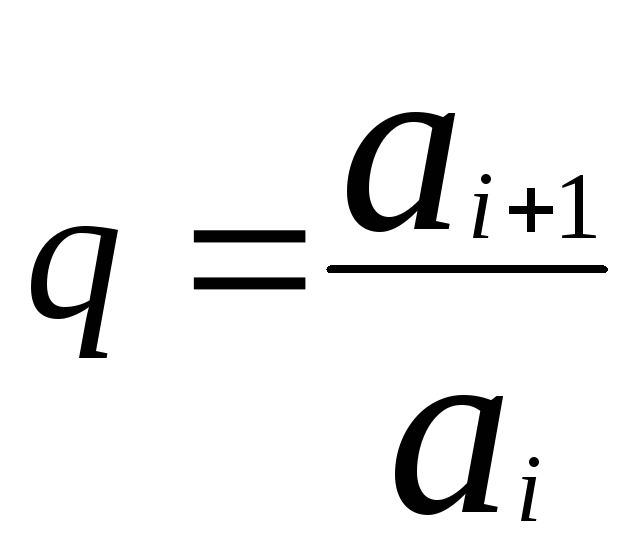. Если эту формулу можно записать в виде выражения на языке программирования, то для решения поставленной задачи применяется следующий метод

1. Переменная, в которой накапливается сумма, обнуляется

F:=0;

2. Текущему числу присваивается предварительно вычисленное первое значение

a:=<первое число>;

3. Фиксируется первый номер числа

i:=1;

4. Пока абсолютная величина очередного числа, входящего в сумму больше заданной точности eps повторяются следующие действия:

а) очередное число добавляется к сумме;

б) вычисляется значение нового числа по рекуррентной формуле – новое число равняется старому значению, умноженному на предварительно выведенную формулу знаменателя геометрической прогрессии;

в) номер числа увеличивается на 1