
- •Законы физики должны быть одинаковыми для всех наблюдателей, движущихся с постоянной скоростью друг относительно друга, независимо от величины и направления скорости.
- •Замедление времени12
- •Преобразование Лоренца
- •Лоренцево сокращение длины
- •Парадокс близнецов
- •Релятивистское сложение скоростей
- •Релятивистские импульс и энергия
- •Энергия системы невзаимодействующих частиц
- •Энергия системы связанных частиц.
Релятивистское сложение скоростей
 «До сих пор мы считали, что предметы
или частицы покоятся в одной системе
координат и движутся со скоростью v
в другой. Рассмотрим теперь случай,
когда в одной из систем отсчёта предмет
имеет скорость ux,
а в другой ux΄.
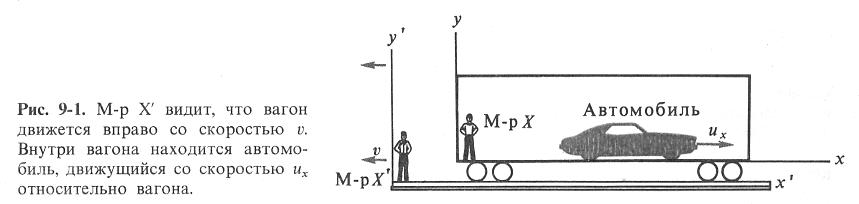
На рис 9-1 приведён пример ситуации такого
типа, в которой по измерениям м-ра X
скорость автомобиля ux,
а по измерениям м-ра Х΄ он движется
быстрее – со скоростью ux΄.
В классической механике ux΄=
ux+
v. Релятивистское
правило сложения скоростей получается
с помощью преобразований Лоренца,
записанных в дифференциальной форме:
dx΄=γdx+γvdt,
dt΄=γdt+(γv/c2)dx.
Разделим первое уравнение на второе:
«До сих пор мы считали, что предметы
или частицы покоятся в одной системе
координат и движутся со скоростью v
в другой. Рассмотрим теперь случай,
когда в одной из систем отсчёта предмет
имеет скорость ux,
а в другой ux΄.
На рис 9-1 приведён пример ситуации такого
типа, в которой по измерениям м-ра X
скорость автомобиля ux,
а по измерениям м-ра Х΄ он движется
быстрее – со скоростью ux΄.
В классической механике ux΄=
ux+
v. Релятивистское
правило сложения скоростей получается
с помощью преобразований Лоренца,
записанных в дифференциальной форме:
dx΄=γdx+γvdt,
dt΄=γdt+(γv/c2)dx.
Разделим первое уравнение на второе:
![]()
![]() .
.
Обозначая dx/dt и dx΄/dt΄ соответственно через ux и ux΄, получаем:
ux΄=
![]() .
.
Это соотношение называется релятивистским (или эйнштейновским) правилом сложения скоростей. Очевидно, результирующая скорость меньше суммы двух скоростей ux и v. Однако если обе скорости малы по сравнению со скоростью света, то результирующая скорость очень близка к сумме скоростей.
Если теория непротиворечива, то полученное выражение должно запрещать скорости больше чем с. Допустим, что в нештрихованной системе отсчёта частица движется уже со скоростью света (это может быть частица света – фотон); таким образом, ux=c. При этом наблюдатель в штрихованной системе обнаружит, что
![]() .
.
Мы видим, что свет (или что-то другое), распространяющийся со скоростью с, должен казаться имеющим эту же скорость всем наблюдателям – независимо от того, сколь быстро они движутся. Как указывалось ранее, уравнения Лоренца преобразуют время и пространство таким образом, что свет распространяется с одинаковой скоростью с с точки зрения всех наблюдателей.
Предположим, что автомобиль на рис. 9-1 движется теперь влево со скоростью, равной по величине u. Чему тогда равна скорость автомобиля в штрихованной системе отсчёта? В данном случае ux=-u. Тогда релятивистское правило сложения скоростей примет вид:
![]() .
.
Этот результат относится к случаю, когда скорости ux и v имеют противоположные знаки.»
Релятивистские импульс и энергия
В СТО импульс даётся выражением:![]() ,
где
,
где
![]() - скорость тела. Именно это выражение
для импульса обеспечивает выполнение
фундаментального закона сохранения
импульса в рамках СТО. И ещё, видно, что
до тех пор , пока скорость тела значительно
меньше скорости света, приведённое
здесь выражение для импульса практически
совпадает с выражением для импульса в
классической физике:
- скорость тела. Именно это выражение
для импульса обеспечивает выполнение
фундаментального закона сохранения
импульса в рамках СТО. И ещё, видно, что
до тех пор , пока скорость тела значительно
меньше скорости света, приведённое
здесь выражение для импульса практически
совпадает с выражением для импульса в
классической физике:
![]() .
.
В СТО вводится также новое определение
энергии (полной):
![]() .
Это выражение также обеспечивает
выполнение фундаментального закона
сохранения энергии в рамках СТО, в
частности, при переходе из нештрихованной
системы отсчёта в штрихованную. Посмотрим
теперь , к чему приведёт новое определение
энергии в «классическом пределе», т. е.
при скоростях, значительно меньших, чем
скорость света:
.
Это выражение также обеспечивает
выполнение фундаментального закона
сохранения энергии в рамках СТО, в
частности, при переходе из нештрихованной
системы отсчёта в штрихованную. Посмотрим
теперь , к чему приведёт новое определение
энергии в «классическом пределе», т. е.
при скоростях, значительно меньших, чем
скорость света:
![]() для u/c<<1.
Здесь было использовано биномиальное
разложение:
для u/c<<1.
Здесь было использовано биномиальное
разложение:
![]() .
Таким образом в пределе малых скоростей
эйнштейновская энергия принимает вид
.
Таким образом в пределе малых скоростей
эйнштейновская энергия принимает вид
![]() .
Заметим, что второе слагаемое – это
классическая энергия свободной частицы
с массой m и скоростью
u. Следовательно,
данное Эйнштейном определение энергии
согласуется с классической механикой,
если к кинетической энергии прибавить
постоянную величину mc2.
В классической механике аддитивная
постоянная в выражении для энергии
может быть выбрана совершенно произвольно,
однако в теории Эйнштейна это уже не
так. В 1905 году Эйнштейн пришёл к выводу
о том, что частица в состоянии покоя
обладает запасом энергии E0=mc2;
он назвал её энергией покоя (или
собственной энергией). С тех пор получено
огромное число подтверждений такого
смелого вывода, и одно из них –
существование атомной бомбы.
.
Заметим, что второе слагаемое – это
классическая энергия свободной частицы
с массой m и скоростью
u. Следовательно,
данное Эйнштейном определение энергии
согласуется с классической механикой,
если к кинетической энергии прибавить
постоянную величину mc2.
В классической механике аддитивная
постоянная в выражении для энергии
может быть выбрана совершенно произвольно,
однако в теории Эйнштейна это уже не
так. В 1905 году Эйнштейн пришёл к выводу
о том, что частица в состоянии покоя
обладает запасом энергии E0=mc2;
он назвал её энергией покоя (или
собственной энергией). С тех пор получено
огромное число подтверждений такого
смелого вывода, и одно из них –
существование атомной бомбы.
При переходе из одной системы отсчёта в другую импульс и энергия преобразовываются в соответствие со следующими выражениями: p΄x=γpx+γβ(E/c), p΄y=py, p΄z=pz, E΄/c=γ(E/c)+γβpx, где E≡mγ(u)c2, E΄≡mγ(u΄)c2 и β≡v/c. Отсюда видно, что четыре величины px, py, pz, E/c преобразуются в точности по тем же формулам, что и четыре величины x, y, z, ct, т. е. с помощью преобразований Лоренца.
В теории относительности определение
кинетической энергии является тем же
самым, что и в классической физике –
это энергия, обусловленная движением
частицы. Для свободной частицы её можно
получить, вычитая из полной энергии
энергию покоя:
![]() .
Как указывалось ранее, если использовать
разложение в ряд по малому параметру,
то в случае скоростей, значительно
меньших, чем скорость света, мы получим
классическое выражение для кинетической
энергии.
.
Как указывалось ранее, если использовать
разложение в ряд по малому параметру,
то в случае скоростей, значительно
меньших, чем скорость света, мы получим
классическое выражение для кинетической
энергии.
Релятивистская масса
Релятивистская масса даётся выражением:
![]() ,
где m – масса покоя
(обычная масса). При данном выше определении
релятивистских импульса и энергии это
выражение не имеет физического смысла,
и большинством серьёзных физиков
отвергается.
,
где m – масса покоя
(обычная масса). При данном выше определении
релятивистских импульса и энергии это
выражение не имеет физического смысла,
и большинством серьёзных физиков
отвергается.
Релятивистская сила
В СТО сила определяется выражением
![]() .
При этом выполняется третий закон
Ньютона. Заметим, что при таком определении
силы, её величина и направление будут
зависеть от скорости движущегося
наблюдателя, тогда как в классической
механике сила не зависит от скорости
наблюдателя.
.
При этом выполняется третий закон
Ньютона. Заметим, что при таком определении
силы, её величина и направление будут
зависеть от скорости движущегося
наблюдателя, тогда как в классической
механике сила не зависит от скорости
наблюдателя.
Релятивистские инварианты
Под инвариантом понимается физическая величина, не меняющаяся при переходе из одной системы отсчёта в другую14.
В СТО, как можно было заметить, при переходе из одной системы отсчёта в другую изменяются координаты тела, время (!), энергия, импульс, сила, значения вектора напряжённости электрического поля и вектора индукции магнитного поля и др. В частности, правила преобразования координат и времени даются т. н. преобразованиями Лоренца. По сходным правилам преобразуются и другие физические величины. Но существуют некие комбинации этих физических величин, имеющие определённый физический смысл, которые остаются неизменными (т. е. они – инварианты) в любых системах отсчёта. Рассмотрим некоторые из них.
Инвариантом является алгебраическая сумма электрических зарядов системы. Этот факт означает, что в СТО действует фундаментальный закон – закон сохранения электрического заряда.
Инвариантом является т. н. интервал:
s=![]() ,
где
,
где
![]() .
Заметим, что в обычной механике инвариантом
является как раз R.
.
Заметим, что в обычной механике инвариантом
является как раз R.
Инвариантом является величина
![]() =
=![]() ,
где Е и
,
где Е и
![]() – полная энергия и импульс частицы
соответственно. Это выражение можно
рассматривать как определение массы.
И масса частицы в СТО – это инвариант.
– полная энергия и импульс частицы
соответственно. Это выражение можно
рассматривать как определение массы.
И масса частицы в СТО – это инвариант.
Инвариантом является величина Е2-с2В2,
где
![]() - вектор напряжённости электрического
поля, а
- вектор напряжённости электрического
поля, а
![]() -
вектор индукции магнитного поля. Отсюда
следует вывод: единой физической
реальностью является электромагнитное
поле, а не отдельно взятые электрическое
и магнитное поля15.
Можно так выбрать систему отсчёта
(например, такую, где заряд покоится),
что
будет равно нулю, но в другой системе
отсчёта обнаруживаются оба вектора: и
,
и
.
-
вектор индукции магнитного поля. Отсюда
следует вывод: единой физической
реальностью является электромагнитное
поле, а не отдельно взятые электрическое
и магнитное поля15.
Можно так выбрать систему отсчёта
(например, такую, где заряд покоится),
что
будет равно нулю, но в другой системе
отсчёта обнаруживаются оба вектора: и
,
и
.
