Примеры решения задач

Задача 6.1. Луч МN, не параллельный главной оптической оси, падает на собирающую линзу, фокус которой известен. Постройте дальнейший ход луча через линзу.

Решение. Через центр линзы С проводим побочную оптическую ось KC || MN, которая пересекается с фокальной плоскостью аb в точке – побочном фокусе линзы (рис. 6.10). Соединив точки N и , находим направление дальнейшего хода луча.

Задача 6.2. Докажите, что оптическая сила двух соприкасающихся тонких линз равна сумме их оптических сил.

Решение. Предположим, что вторая линза более длиннофокусная ( ), а так же, что обе линзы – собирающие (рис. 6.11)

Пусть источник света находится слева в фокусе первой линзы ( ). Пучок света, пройдя первую линзу, далее распространяется параллельно главной оптической оси. Этот пучок, попав на вторую линзу, сходится в ее фокусе, т. е. . Таким образом, для системы из двух линз получаем

, или

Подставляя , получим

.

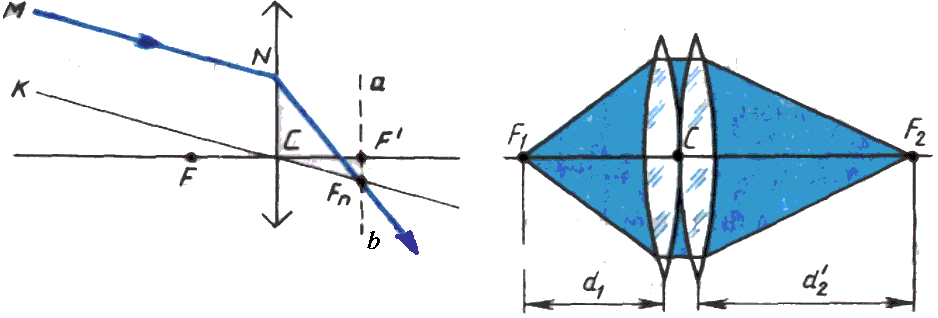
Рис. 6.10 Рис. 6.11

Задача 6.3. Предмет расположен на расстоянии 40 см от линзы, имеющей оптическую силу 5 дптр. Вторая линза с оптической силой 6 дптр расположена на расстоянии 60 см от первой линзы. Определите, где находится изображение н каково поперечное увеличение, даваемое оптической системой.

Решение. Построим изображение предмета в первой линзе (рис. 6.12). По формуле линзы имеем:

, откуда

Считая это изображение предметом для второй линзы, находим расстояние до нее: . По формуле находим расстояние от второго изображения до второй линзы:

Первая линза дает изображение, равное предмету, поскольку и . Увеличение дает только вторая линза. Отсюда определяем увеличение, даваемое всей оптической системой:

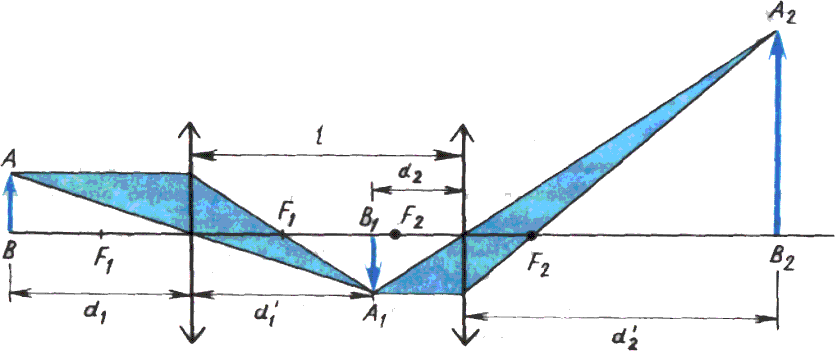
Рис. 6.12

3Адача 6.4. На каком расстоянии от собирающей линзы с фокусным расстоянием 20 см нужно расположить предмет, чтобы получить изображение, увеличенное в 4 раза?

Решение. Увеличение , отсюда . Подставляем это соотношение в формулу тонкой линзы:

;

Задача 6.5. Даны положения главной оптической оси собирающей линзы, светящейся точки S и ее изображения S' (рис. 6.13, а). Найдите построением положение оптического центра и фокуса линзы.

Решение. Проводим отрезок прямой, соединяющий светя­щуюся точку и ее изображение (рис. 6.13, б). Точка пересечения С главной оптической оси с этой прямой является оптическим центром линзы. Через эту точку перпендикулярно главной опти­ческой оси проводим главную плоскость линзы. Затем из точки S проводим отрезок прямой параллельно главной оптической оси до пересечения с главной плоскостью в точке A. Соединяя точки А и S', определяем положение главного фокуса линзы F. Построив S'А' параллельно главной оптической оси и соединив A' и S, получим положение второго главного фокуса F'. Нетрудно доказать, что .

З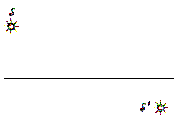 адача 6.6. Оптическая система состоит из двух собирающих линз с фокусными расстояниями и , расположенных на расстоянии друг от друга. Определите, на каком расстоянии от второй линзы

Рис. 6.13 а) расположен фокус этой оптической системы.

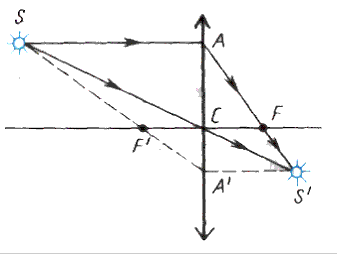
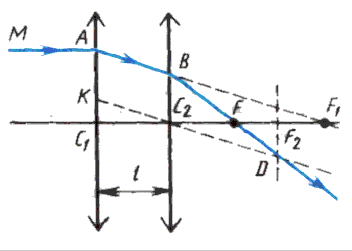
Рис. 6.13 а) и б) Рис. 6.14

Решение. Определим графически, где находится фокус системы (рис. 6.14). Для этого направим на левую линзу параллельный пучок (луч МА), который (если бы не было второй линзы) собрался бы в точке . Однако присутствие второй линзы приводит к тому, что этот пучок сходится в точке F, которую находим следующим образом: проводим луч KC₂ || АВ, находим его пересечение с фокальной плоскостью второй линзы в точке D и на пересечении луча ВD с главной оптической осью находим точку F. Рассматриваем образовавшиеся треугольники. Анализ рисунка 6.14 показывает, что здесь есть подобные треугольники:

и

Из подобия треугольников следует:

и .

Разделив первое соотношение на второе, получим:

, откуда

Заметим, что из полученной формулы получается результат решения задачи 6.2, если положить . Докажите это.

Задача 6.7. На горизонтально расположенное вогнутое зеркало с радиусом кривизны 0,5 м налили воду. Какова оптическая сила этой системы?

Решение. Данная оптическая система состоит из вогнутого зеркала с радиусом кривизны R = 0,5 м и плосковыпуклой водя­ной линзы с показателем преломления и радиусами кри­визны м и (рис. 6.15). Поскольку оба опти­ческих прибора сложены вплотную, то их оптическая сила равна их сумме (см. задачу 6.2). При этом следует учесть, что через линзу свет проходит дважды – при падении на зеркало и отраже­нии от него. Имеем:

Задача 6.8. Двояковыпуклая линза из стекла ( ) с радиусами кривизны помещена в сероуглерод ( ). Определите оптическую силу линзы.

Решение. Оптическую силу найдем по формуле (6.7), где относительный показатель преломления . Тогда

Как видно, в данном случае двояковыпуклая линза оказывается рассеивающей.

Задача 6.9. Через отверстие в непрозрачном экране проходит сходящийся пучок, собирающийся в точке А, находящейся от экрана на расстоянии AC=42 см. Если в отверстие вставить собирающую линзу с фокусным расстоянием 21 см, то пучок соберется в точке А' (рис. 6.16). Определите расстояние А'С.

Решение. Точка А является «мнимым предметом» для действительного изображения А'. Имеем. Подставив в формулу линзы (6.3) значения величин, получим:

или

Отсюда

.

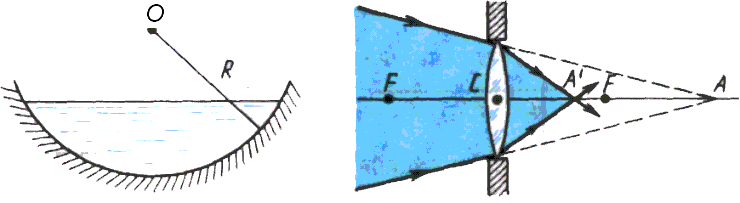
Рис. 6.15 Рис. 6.16