11

Геометрическая оптика

Геометрическая оптика – это раздел классической физики, где принципиально не ставится вопрос, что такое свет, а, основываясь на определённой концепции, рассматриваются с единой точки зрения некоторые (не всё!) оптические явления. Следует сразу подчеркнуть, что геометрическая оптика - это частная, приближённая теория; целый ряд оптических явлений геометрическая оптика объяснить не в состоянии. Тем не менее, это очень полезная теория, так как при всей своей относительной простоте там, где она «работает», экспериментальные результаты с высокой степенью точности соответствуют теоретическим расчётам.

Содержание

1. Основные понятия геометрической оптики……………………………………….1

2. Принцип Ферма, законы отражения и преломления…………………………….. 3

3. Призма как оптический прибор…………………………………………………… 5

4. Полное отражение………………………………………………………………….. 6

5. Зеркала……………………………………………………………………………….12

6. Линзы……………………………………………………………………………….. 16

7. Глаз как оптическая система………………………………………………………. 25

8. Приборы, увеличивающие угол зрения…………………………………………... 30

9. Фотоаппарат, проектор…………………………………………………………….. 35

Приложение. Элементы волновой оптики, законы отражения и преломления……. 37

1. Основные понятия геометрической оптики

Первые оптические приборы и устройства, основанные на идеях геометрической оптики, появились много столетий назад. Создавались они искусными умельцами, обладавшими не только умелыми руками, но и большой наблюдательностью. Первые линзы и телескопы были сделаны на основе расчетов и предшествующего опыта. Расчеты велись с помощью законов геометрической оптики: закона прямолинейного распространения света в однородной среде, законов отражения и преломления света, полученных опытным путем. При этом использовались понятия «световой пучок» и «световой луч», причем последний рассматривался как бесконечно тонкий пучок. Были разработаны весьма изящные методы расчета оптических систем на основе этих понятий и законов. Эти методы сохранили свое значение и после того, как была выяснена волновая природа света.

В приложении показано, как законы отражения и преломления света можно вывести с помощью принципа Гюйгенса исходя из волновой теории. С помощью принципа Гюйгенса – Френеля можно решить вопрос и о прямолинейном распространении света. Выясним, как же соотносится понятие светового пучка, проходящего через диафрагму, с явлением дифракции света - явления, наблюдаемого экспериментально, но не объяснимого с точки зрения геометрической оптики.

Световой пучок и дифракция. Пусть на диафрагму-отверстие падает нормально параллельный пучок света; с волновой точки зрения это означает, что на экран 1 падает плоская волна (рис. 1.1). Если исходить из представлений геометрической оптики, в частности из закона прямолинейного распространения света, то на экране 2 должно получиться световое пятно точно такого же диаметра, как и отверстие.

Опыт показывает, что если диаметр отверстия (диафрагмы) достаточно велик, а расстояние между экранами L не очень велико, то мы получаем ожидаемый результат. Но если отверстие не очень велико, а расстояние между диафрагмой и экраном большое, то пятно на экране расширяется; кроме того, на краях пятна наблюдается чередование светлых и темных колец – интерференционных максимумов и минимумов.

Причина очевидна – сказывается явление дифракции света (см. соответствующие разделы волновой оптики). Исходя из этого опыта, попытаемся выяснить, когда дифракцией можно пренебречь и когда она явно проявляется.

Как известно, дифракционный угол φ между направлениями на центральный максимум и ближайший к нему первый ми­нимум можно найти из приближенного соотношения .

Риc. 1.1 Риc. 1.2

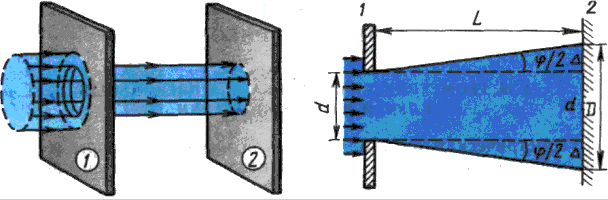
Из рисунка 1.2 видно, что ширина пятна на экране 2 равна D = d+2∆, где ∆ = L tg (φ/2). Учитывая, что длина световой волны очень мала (λ≈0,5 мкм), т.е. λ∙ d, можно считать, что . Тогда φ≈λ/d и ∆≈Lφ/2 = Lλ/(2d) . Поэтому для диаметра пятна будем иметь:

(1.1)

Из соотношения (1.1) следуют важные выводы.

1) Дифракция не наблюдается, если Lλ/d<<d. В этом случае D≈d, т.е. свет распространяется прямолинейно, как и должно быть в соответствии с положениями геометрической оптики.

Таким образом, закон прямолинейности распространения света оказывается приближенным законом. Им можно пользоваться, если выполняется неравенство

(1.2)

2) Дифракция наблюдается, если . В этом случае , т. е. размер пятна на экране 2 много больше размера отверстия диафрагмы, и закон прямолинейности распространения света нарушается. Дифракция на диафрагме будет хорошо наблюдаться, если справедливо неравенство

(1.3)

Это условие определяет границы применимости геометричес­кой оптики.

Пучок и луч. Иногда говорят, что луч – это очень узкий пучок света. Данное утверждение – принципиально ложно.

В самом деле, представим себе, что имеется диафрагма, диаметр которой мы можем неограниченно уменьшать. Пока выполняется условие (1.2), пучок остается параллельным и слабо расходится. Но по мере уменьшения диаметра диафрагмы второе слагаемое в выражении (1.1) возрастает, и при условии, например, пятно на экране станет вдвое шире, т.е. .

Итак, сжимая пучок света путем уменьшения размера диафрагмы, мы получаем обратный эффект: пучок не только не сжимается, но, наоборот, за счет дифракции расширяется. Отсюда следует, что бесконечно узких световых пучков не бывает! Этот результат – следствие волновой природы света.

Что же такое луч? Это не физическая модель, а чисто геометрическое понятие. Луч – это направление, в котором световой волной переносится энергия, это перпендикуляр к фронту световой волны. До создания волновой оптики луч считали физическим объектом, и эта терминология по традиции сохраняется, иногда и в учебниках, а особенно в быту и популярной литературе. С этим приходится мириться, но при этом следует помнить, что реальными физическими объектами являются световая волна и световой пучок. Световой луч – это полезное геометрическое понятие, облегчающее решение ряда задач методами геометри­ческой оптики.