
- •Практическое занятие 9 Метод потенциалов решения транспортной задачи
- •Алгоритм метода потенциалов.
- •(Ден. Единиц);
- •Примеры для самостоятельного решения
- •2. Менеджер отдела логистики составляет план перевозок продукции фирмы с четырех ее складских комплексов к четырем клиентам. Составьте план перевозок, минимизирующий издержки
Практическое занятие 9 Метод потенциалов решения транспортной задачи
В
симплекс-методе для нахождения нового
базиса и принятия решения об оптимальности
опорного плана используется
величина
 .
В методе потенциалов предлагается
другой прием, уменьшающий объем
вычислений. Для этого вводится понятие
цикла транспортной задачи.
.
В методе потенциалов предлагается
другой прием, уменьшающий объем
вычислений. Для этого вводится понятие
цикла транспортной задачи.
Циклом
в таблице условий транспортной задачи
(табл.15) называется замкнутая ломаная,
состоящая из звеньев, расположенных
вдоль строк и столбцов, все вершины
которой, кроме одной, расположены в
занятых клетках таблицы. Для любой
свободной клетки, то есть клетки, где
на месте
 находится прочерк, можно построить лишь
один цикл.
находится прочерк, можно построить лишь
один цикл.
Суть
метода потенциалов заключается в том,
что после нахождения опорного плана
каждому поставщику (строке) ставится в
соответствие число
 ,
называемое потенциалом поставщика
,
называемое потенциалом поставщика
 ,
а каждому потребителю (столбцу) – число
,
а каждому потребителю (столбцу) – число
 ,
называемое потенциалом потребителя.
Числа
и
выбирают так, чтобы в любой занятой
клетке
выполнялось равенство
,
называемое потенциалом потребителя.
Числа
и
выбирают так, чтобы в любой занятой
клетке
выполнялось равенство
 .
.
Если
план
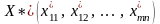 транспортной задачи является оптимальным,
то ему соответствует система из
транспортной задачи является оптимальным,
то ему соответствует система из
 чисел
чисел
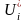 и
и
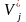 ,
удовлетворяющих условиям
,
удовлетворяющих условиям
 для
для
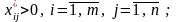 (1)
(1)
 для
для
 (2)
(2)
Необходимое
и достаточное условие оптимальности
плана транспортной задачи в
том, что ему должны соответствовать
числа
и
,
удовлетворяющие условиям
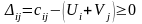 для свободных и
для свободных и
 для занятых клеток.
для занятых клеток.
Потенциалы
находят из условия
,
где
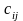 – стоимость перевозки единицы груза,
указанная в i-ой
строке и j-м
столбце занятой клетки. Опорный план
задачи содержит
– стоимость перевозки единицы груза,
указанная в i-ой
строке и j-м
столбце занятой клетки. Опорный план
задачи содержит
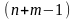 линейно независимых уравнений вида
(53) с
линейно независимых уравнений вида
(53) с
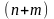 неизвестными. Число уравнений (число
занятых клеток
неизвестными. Число уравнений (число
занятых клеток
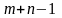 )
на единицу меньше числа неизвестных,
поэтому одному неизвестному (обычно
)
на единицу меньше числа неизвестных,
поэтому одному неизвестному (обычно
 )
придают нулевое значение. Тогда остальные
потенциалы определяются однозначно.
Если
в транспортной задаче число положительных
компонент
опорного плана
)
придают нулевое значение. Тогда остальные
потенциалы определяются однозначно.
Если
в транспортной задаче число положительных
компонент
опорного плана
 ,
то его называют вырожденным.
,
то его называют вырожденным.
Алгоритм метода потенциалов.
Находят первоначальный опорный план одним из рассмотренных методов.
Проверяют, будет ли число занятых клеток . Если это условие не выполнено, то опорный план вырожденный, недостающее число клеток заполняют нулевыми перевозками
 .
.Вычисляют потенциалы и из условия, что для занятых клеток , при этом приравнивают нулю.
Для каждой свободной клетки определяют величину
 .
Если все
.
Если все
 ,
полученный план является оптимальным.
Если
,
полученный план является оптимальным.
Если
 ,
этот план единственный. Если хотя бы
одно
,
этот план единственный. Если хотя бы
одно
 ,
задача имеет бесконечное множество
оптимальных планов. Если хотя бы одна
оценка
,
задача имеет бесконечное множество
оптимальных планов. Если хотя бы одна
оценка
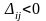 ,
переходят к пункту 5.
,
переходят к пункту 5.Находят значение , максимальное по модулю. Для соответствующей свободной клетки строят замкнутый цикл пересчета. Пусть
 .
Построенный цикл обходят против часовой
стрелки, присваивая вершинам по очереди
знаки "+" и "–", начиная с
клетки
.
Построенный цикл обходят против часовой
стрелки, присваивая вершинам по очереди
знаки "+" и "–", начиная с
клетки
 .
Среди клеток с отрицательным знаком
выбирают ту, в которую поставляется
меньше всего груза.
.
Среди клеток с отрицательным знаком
выбирают ту, в которую поставляется
меньше всего груза.
Пусть
 .
Тогда количество груза, равное
.
Тогда количество груза, равное
 ,
вычитают из клеток, отмеченных знаком
"–", и прибавляют в клетках,
отмеченных знаком "+". Так перемещают
груз по вершинам цикла и получают новый
опорный план. Для него вычисляют величину
расходов на перевозку и переходят к
пункту 3.
,
вычитают из клеток, отмеченных знаком
"–", и прибавляют в клетках,
отмеченных знаком "+". Так перемещают
груз по вершинам цикла и получают новый
опорный план. Для него вычисляют величину
расходов на перевозку и переходят к
пункту 3.
Если при перемещении груза по вершинам цикла отрицательных вершин с одинаковым значением несколько, то освобождают только одну вершину, а остальные считают занятыми с поставками груза , равными нулю. Занятые клетки, не являющиеся вершинами замкнутого цикла, переписывают, не меняя.
С
экономической точки зрения клетка,
которой отвечает значение
 ,
является наиболее «перспективной»,
ведущей к максимальному удешевлению
транспортных издержек, так как
,
является наиболее «перспективной»,
ведущей к максимальному удешевлению
транспортных издержек, так как
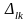 показывает, на сколько единиц уменьшатся
транспортные расходы при поставке в
клетку
одной единицы груза. При поставке груза
в количестве
единиц транспортные расходы уменьшатся
на величину
показывает, на сколько единиц уменьшатся
транспортные расходы при поставке в
клетку
одной единицы груза. При поставке груза
в количестве
единиц транспортные расходы уменьшатся
на величину
 .
.
Пример 3. Найти оптимальный план транспортной задачи, исходные данные которой приведены в табл.20. Таблица 20
|
|
|||
30 |
30 |
10 |
20 |
|
50 |
1
|
2
|
4
|
1
|
30 |
2
|
3
|
1
|
5
|
10 |
3
|
2
|
4
|
4
|
Решение.
Проверим закрытость модели:
 .
.
Составим
первоначальный опорный план, используя
метод северо-западного угла. Число
занятых клеток должно быть 3 + 4 – 1 = = 6.
Для занятых клеток найдем потенциалы
поставщиков и потребителей
и
,
принимая
 .
Получим табл. 21.
.
Получим табл. 21.
Таблица 21
|
|
|
||||
30 |
30 |
10 |
20 |
|||
50 |
1 30 |
– 2 2 |
4
|
+ 1
|
0 |
|
30 |
2
|
+ 3 10 |
1 10 |
– 5 10 |
1 |
|
10 |
3
|
2
|
4
|
4 10 |
0 |
|
|
1 |
2 |
0 |
4 |
|
|
Найдем транспортные издержки и оценки для свободных клеток:



 0
0