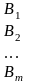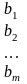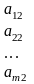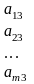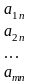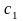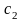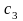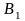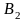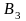Практическое занятие 1 Математические модели задач математического программирования
Математическое моделирование – это изучение явления или процесса с помощью математической модели, т.е. математического описания изучаемого процесса, которое с достаточной степенью точности, но упрощенно отражает действительный процесс или явление.
Для составления математической модели следует:
Выбрать для задачи переменные величины
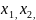 ...
... ,
которые полностью характеризуют
описываемый процесс;
,
которые полностью характеризуют
описываемый процесс;Составить систему ограничений, представляющих совокупность уравнений и неравенств, которым удовлетворяют переменные задачи;
Задать целевую функцию L(X)= f( ...
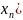 переменных задачи, которая характеризует
качество выполнения задачи , экстремум
которой необходимо найти.
переменных задачи, которая характеризует
качество выполнения задачи , экстремум
которой необходимо найти.
Если целевая функция и система ограничений линейны, то задача математического программирования называется задачей линейного программирования (ЗЛП).
В общем случае она формулируется так:
Найти переменные ... , доставляющие экстремум целевой функции
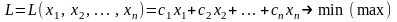 ;
(1)
;
(1)
и удовлетворяющие системе ограничений :
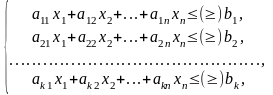 (2)
(2)
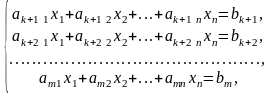 (3)
(3)
 ,
,
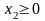 ,
… ,
,
… ,
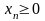 .
(4)
.
(4)
Вектор
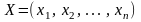 ,
удовлетворяющий условиям (2)-(4), называется
допустимым
планом ЗЛП.
,
удовлетворяющий условиям (2)-(4), называется
допустимым
планом ЗЛП.
Опорный
план
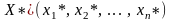 ,
доставляющий
минимум (максимум) целевой функции
, называют оптимальным
решением ЗЛП.
,
доставляющий
минимум (максимум) целевой функции
, называют оптимальным
решением ЗЛП.
Рассмотрим примеры составления математических моделей некоторых управленческих задач:
1. Задача оптимального производственного планирования. Для изготовления п видов продукции используют m видов сырья. Запасы сырья, количество единиц сырья, затрачиваемых на изготовление единицы продукции, а также величина прибыли, получаемая от реализации единицы продукции, приведены в табл.1. Необходимо составить такой план выпуска продукции, чтобы от её реализации получить максимальную прибыль.
Таблица 1
Вид сырья |
Запас сырья |
Количество единиц сырья, необходимого для изготовления единицы продукции |
||||||||
1 |
2 |
3 |
… |
n |
||||||
|
|
|
|
|
|
|
||||
Прибыль от единицы продукции |
|
|
|
|
|
|||||
Обозначим
через
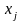 –
количество единиц продукции, планируемой
к выпуску,
–
количество единиц продукции, планируемой
к выпуску,
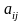 – количество единиц сырья, необходимого
для изготовления единицы продукции,
индекс j
соответствует виду продукции, индекс
– количество единиц сырья, необходимого
для изготовления единицы продукции,
индекс j
соответствует виду продукции, индекс
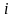 – виду сырья. Учитывая количество единиц
сырья, затрачиваемых на изготовление
единицы продукции, а также объем запасов
сырья, получим систему ограничений
– виду сырья. Учитывая количество единиц
сырья, затрачиваемых на изготовление
единицы продукции, а также объем запасов
сырья, получим систему ограничений
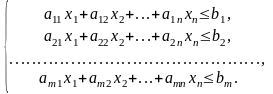
Ее смысл в том, что количество сырья, расходуемое на изготовление продукции, не может превысить имеющихся запасов. Исходя из экономического смысла задачи, переменные не могут быть отрицательными
≥ 0,
j
=
 .
.
Конечная
цель решаемой задачи – получить
максимальную прибыль. Она описывается
линейной функцией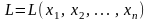
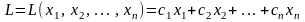 .
.
Итак, математическая модель рассматриваемой экономической задачи имеет вид
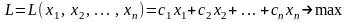 ;
;
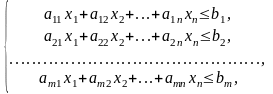
, , … , .
2. Задача о диете, или задача об оптимальном составе смеси. Такие задачи возникают при смешивании различных компонент для получения смеси, удовлетворяющей определённым требованиям. Например, при получении наиболее экономичной смеси горючего для двигателей различных типов; составлении экономичной шихты для выплавки чугуна и стали. Задачи на смеси приходится решать при определении рациональных норм потребления продуктов питания, при планировании снабжения продуктами питания детских учреждений, больниц и т.д. Эти задачи возникают в животноводстве при составлении оптимального рациона откорма скота.
Рассмотрим простейшую постановку задачи. В сутки организм человека нуждается в m видах питательных веществ A1 , A2 , …, Am в количествах не менее b1, b2, … , bm соответственно. Эти питательные вещества содержатся в п видах продуктов B1 , B2 , …, Bn . Известно, что в одной единице продукта Bj содержание питательного вещества Аi, составляет aij единиц. Стоимость единицы продукта Bj составляет cj рублей. Данные задачи представлены в табл.2.
Таблица 2
Питательные вещества |
Норма питательных веществ |
Количество единиц питательных веществ в 1 кг продукта |
|||||||||
|
|
|
… |
|
|||||||
|
|
|
|
|
|
|
|||||
Стоимость 1 кг продукта |
|
|
|
|
|
||||||
Необходимо составить дневной рацион питания (меню) так, чтобы затраты на него были минимальными.
Пусть – количество продукта вида j, входящего в дневной рацион. Используем обозначения, приведённые в табл.2. Получаем систему ограничений
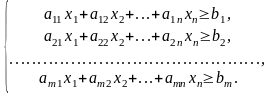
По
смыслу задачи следует, что
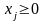 ,
j
=
.
,
j
=
.
Требование составить дневной рацион питания необходимого качества с минимальными затратами приводит к условию
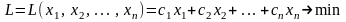 .
.
Итак, для составления оптимального суточного меню нужно решить следующую задачу линейного программирования
;
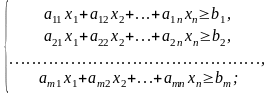
, j = .
3. Задача о рациональной организации снабжения промышленного центра однородным продуктом.
Требуется
организовать снабжение промышленного
центра картофелем или углем. Продукт
может привозиться в центр из
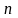 пунктов. Пусть
пунктов. Пусть
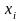 –
количество продукта, поставляемое в
центр из
-го
пункта, а
–
количество продукта, поставляемое в
центр из
-го
пункта, а
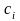 –
суммарная стоимость производства и
перевозки единицы продукта из
-го
пункта. Тогда стоимость продукта,
доставленного из
-го
пункта в центр, равна
–
суммарная стоимость производства и
перевозки единицы продукта из
-го
пункта. Тогда стоимость продукта,
доставленного из
-го
пункта в центр, равна
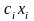 ,
а стоимость продукта, привезенного в
центр из всех пунктов производства,
равна
,
а стоимость продукта, привезенного в
центр из всех пунктов производства,
равна
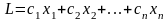 .
(5)
.
(5)
Снабжение
надо организовать так (выбрать
),
чтобы обеспечить минимальную стоимость
продукта в центре. При этом нужно учесть,
что потребность центра в продукте,
определяемая величиной
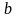 ,
должна быть удовлетворена, но излишков
быть не должно. Следовательно, искомые
переменные должны удовлетворять условию:
,
должна быть удовлетворена, но излишков
быть не должно. Следовательно, искомые
переменные должны удовлетворять условию:
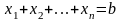 .
(6)
.
(6)
Производство
продуктов в
-м
пункте ограничено величиной
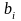 ,
а пропускная способность транспорта,
который может быть использован для
перевозки продукта из
-го
пункта, ограничена величиной
,
а пропускная способность транспорта,
который может быть использован для
перевозки продукта из
-го
пункта, ограничена величиной
 .
Пусть
.
Пусть
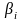 меньшее из двух чисел
меньшее из двух чисел

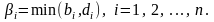
Искомые переменные должны удовлетворять ограничениям
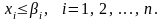 (7)
(7)
Кроме того, значения должны быть неотрицательны: перевозка продукта из центра в пункты его производства исключена
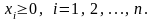 (8)
(8)
Если перевозка продукта из -го пункта может быть обеспечена двумя видами транспорта, то -й пункт целесообразно рассматривать как два пункта с разной стоимостью продукта.
Итак,
мы пришли к задаче линейного
программирования: необходимо обратить
в минимум линейную функцию
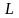 при линейных условиях (5) – (8).
при линейных условиях (5) – (8).