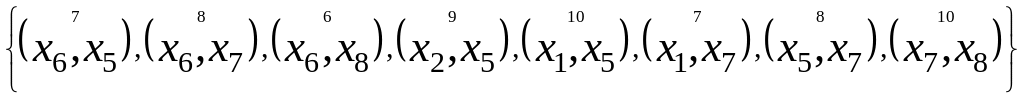4. Содержание отчета

1. Условие задачи в соответствии с вариантом.

2. Определение числа вершин.

3. Определение числа ребер.

4. Определение степени всех вершин.

5. Определение числа компонент связности.

6. Определение цикломатического числа.

7. Определение хроматического числа.

8. Определение плотности и неплотность графа.

9. Определение числа внешней и внутренней устойчивости.

Вычисление всех числовых характеристик графа расписать подробно по этапам.

5. Список литературы

1. Пономарев В.Ф. Дискретная математика для инженеров.- Калининград: ФГОУ ВПО КГТУ, 2010.- 351 с.

Расчетно-графическая работа №7 Тема: «Нахождение кратчайшего остова неориентированного графа по алгоритму Дейкстра».

1. Теоретическая часть

Пусть в качестве задания сформирован граф на рисунке 7.1.

Ребра графа G взвешены количественными значениями весов . В качестве исходной выбрана вершина (она заключена в окружность). Пунктиром обозначены результаты выполнения расчетов (см. ниже).

Построение таблицы обозначений

Для выполнения расчетов построим таблицу 7.1.

Таблица 7.1 ― Обозначения

Ребра графа G	Обозначения ребер	Веса ребра	Обозначения весов ребер графа
1	2	3	4
		3
		10
		7
		9
		4
		3
		5
		2
		3
		4
		5
		7
		5
		8
		6
		8
		10

Шаг «0» расчетов

Поскольку в качестве исходной выбрана вершина , то проанализируем множество смежных с ней вершин:

Так как ребра взвешены весами (указаны над круглыми скобками), выберем ребро с минимальным значением веса . Если таких ребер несколько, то для продолжения вычислений на данном шаге можно выбрать любое из них.

В итоге получим подграф кратчайшего остова, изображенный на рисунке 7.2.

Обведем пунктиром подграф № 1 графа G на рисунке 6.2. В матрице шагов (т.е. в левой части таблицы 6.3) поставим единицы в нулевой строке в столбцах, обозначенных, как и . В таблице 6.4 размера кратчайшего остова графа G поставим единицу в нулевой строке, в столбце, обозначенном весом ребра . В столбце той же нулевой строки укажем .

Шаг «1» расчетов

Зададим в правой части таблицы 7.2 множество ребер инцидентных вершинам подграфа № 1 графа G на рисунке 7.2. Таковых будет семь. Выберем из них ребра с минимальными значениями весов. Таковых два: . Остановим выбор на ребре , что покажем, заключив его в прямоугольник в таблице 7.2. Тогда ребро вычеркнем из данной строки таблица 3. Это ребро используется в дальнейших расчетах.

Таблица 7.3- Размер кратчайшего остова графа G

Шаг p
	3	10	7	9	4	3	5	2	3	4	5	7	5	8	6	8	10
0	0	0	0	0	0	0	0	1	0	0	0	0	0	0	0	0	0	2
1	0	0	0	0	0	0	0	1	1	0	0	0	0	0	0	0	0	5
2	0	0	0	0	0	1	0	1	1	0	0	0	0	0	0	0	0	10
3	1	0	0	0	0	1	0	1	1	0	0	0	0	0	0	0	0	13
4	1	0	0	0	0	1	1	1	1	0	0	0	0	0	0	0	0	18
5	1	0	0	0	0	1	1	1	1	0	0	0	1	0	0	0	0	23
6	1	0	1	0	0	1	1	1	1	0	0	0	1	0	0	0	0	30
Суммарная длина ребер минимального остова графа G:																		30

Таблица 7.2 ― Результаты выбора подграфов графа G

Шаг p	Вершины графа G								Множество ребер графа G, смежных с вычисленным подграфом минимального остова графа G
0	0	0	1	0	0	1	0	0
1	0	0	1	1	0	1	0	0
2	0	1	1	1	0	1	0	0
3	1	1	1	1	0	1	0	0
4	1	1	1	1	1	1	0	0
5	1	1	1	1	1	1	0	1
6	1	1	1	1	1	1	1	1

Шаги «2 – 6» расчетов

Выполняются аналогично расчетам на шаге 1. Особенностью расчетов во время выполнения шагов 2 – 6 оказалось, что на шаге 5 в таблице 7.2 получено множество из восьми ребер. Поскольку присоединение дуг или формировало бы на подграфе кратчайшего остова цикл их необходимо отбросить и остановить выбор на дуге .

Результаты расчетов на шагах 2 – 6 сведены в таблицы 7.2, 7.3. На рисунке 7.4 показано изменение по шагам подграфов минимального остова графа G.

Выводы

Таким образом, в результате расчетов по алгоритму Дейкстра сформирован минимальный остов графа G (см. результаты на шаге 6, рисунок 7.4) с суммарной длиной дуг – 30.

Д обавим к подграфу на рисунке 7.2 ребро и получим подграф № 2 на рисунке 7.3.

Обведем пунктиром подграф № 2 графа G на рисунке 7.1. Заполним первые строки матрицы в таблице 7.3.

Рисунок 7.4 ― Изменение по шагам подграфов минимального остова

графа G