
- •Лекция 13
- •1. Решение произвольных систем линейных уравнений.
- •2. Решение однородных систем.
- •3. Понятие линейного пространства.
- •4. Примеры линейных пространств.
- •5. Евклидово пространство.
- •6. Базис линейного пространства.
- •7. Линейные преобразования.
- •8. Матрица линейного преобразования.
- •9. Собственные векторы и собственные числа.
Лекция 13
1. Решение произвольных систем линейных уравнений.
2. Решение однородных систем.
3. Понятие линейного пространства.
4. Примеры линейных пространств.
5. Евклидово пространство.
6. Базис линейного пространства.
7. Линейные преобразования.
8. Матрица линейного преобразования.
9. Собственные векторы и собственные числа.
1. Решение произвольных систем линейных уравнений.
Рассмотрим систему линейных уравнений (1)
![]() (1)
(1)
Частный
случай если m = n и detA ≠ 0, мы рассмотрели
выше. В общем случае, когда система имеет
размерность (m![]() n)
возникает вопрос о ее совместности.
Ответ на него дает теорема Кронекера –
Капелли.
n)
возникает вопрос о ее совместности.
Ответ на него дает теорема Кронекера –
Капелли.
Рассмотрим
следующие случаи для системы размерности![]() :
:
1.
Пусть ранг равен числу неизвестных
![]() .
В этом случае система имеет единственное
решение. Из теоремы о ранге это означает,
что система имеет r
= n
линейно-
независимых
строк. Тогда рассматривают систему,
состоящую из n
уравнений.
Ее можно решить известными уже методами
(матричным, Крамера или Гаусса). Остальные
m-n
уравнений
можно
отбросить.
.
В этом случае система имеет единственное
решение. Из теоремы о ранге это означает,
что система имеет r
= n
линейно-
независимых
строк. Тогда рассматривают систему,
состоящую из n
уравнений.
Ее можно решить известными уже методами
(матричным, Крамера или Гаусса). Остальные
m-n
уравнений
можно
отбросить.
2.
Если
![]() система в этом случае имеет множество
решений. Оставляют только r
уравнений.
Остальные m-r
уравнений отбрасывают. В оставленных
r уравнениях
слева оставляют
те неизвестные, коэффициенты при которых
вошли в базисный минор.
Остальные
неизвестные n-r
переносят вправо и считают их свободными.
система в этом случае имеет множество
решений. Оставляют только r
уравнений.
Остальные m-r
уравнений отбрасывают. В оставленных
r уравнениях
слева оставляют
те неизвестные, коэффициенты при которых
вошли в базисный минор.
Остальные
неизвестные n-r
переносят вправо и считают их свободными.
Пример.
Решить систему. Размерность системы
![]() .
.
![]() видно,
что
видно,
что
![]() тогда по теореме о ранге
тогда по теореме о ранге
![]() и ранг расширенной матрицы также будет
и ранг расширенной матрицы также будет
![]() то есть ранг системы r
равен 2. Система совместна по теореме
Кронекера - Капелли. Найдем минор второго
порядка не равный нулю.
то есть ранг системы r
равен 2. Система совместна по теореме
Кронекера - Капелли. Найдем минор второго
порядка не равный нулю.
![]()


 выделен
базисный минор.
выделен
базисный минор.
Поскольку
r<n
(n=4,
r=2)
то система имеет
множество
решений.
Это
соответствует
второму случаю, согласно которому
оставим r=2
уравнения, одно уравнение (m-r=3-2=1)
отбросим. В оставленных уравнениях
неизвестные
![]() ,
коэффициенты при которых вошли в базисный
минор, оставим слева, остальные неизвестные
,
коэффициенты при которых вошли в базисный
минор, оставим слева, остальные неизвестные
![]() будем считать свободными.
будем считать свободными.
Сложим
и найдем
![]()
![]() .
Затем из первого найдем
.
Затем из первого найдем
![]() .
.
![]()
![]()
или
![]() или
или
![]() задавая
различные значения
задавая
различные значения
![]() и
и
![]() получим
множество решений.
получим
множество решений.
2. Решение однородных систем.
Опр. Система вида
![]() называется
однородной все bi
=0.
называется
однородной все bi
=0.
Однородная
система всегда совместна, так как
![]() .
Рассмотрим следующие случаи:
.
Рассмотрим следующие случаи:
Если
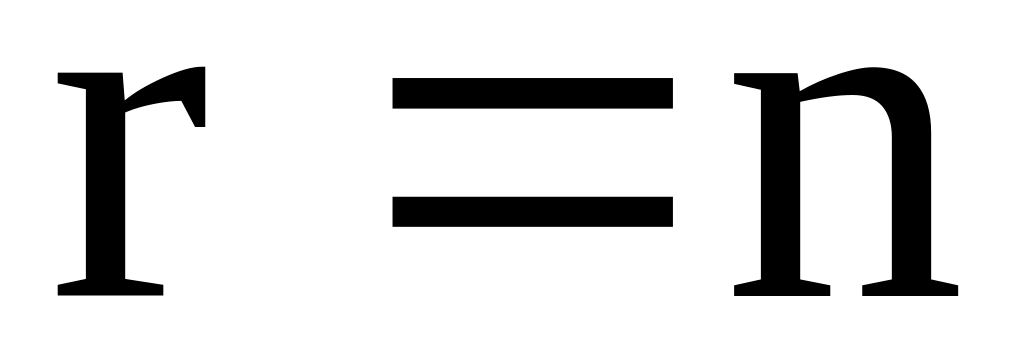 система имеет единственное решение,
называемое тривиальным, то есть нулевым.
система имеет единственное решение,
называемое тривиальным, то есть нулевым.Если r<n то система имеет бесконечное множество решений.
Пример. Решить систему.
![]() строки
линейно зависимы
строки
линейно зависимы
![]() следовательно ранг r=2.
Так как r<n
то система
имеет множество решений. Найдем базисный
минор
следовательно ранг r=2.
Так как r<n
то система
имеет множество решений. Найдем базисный
минор
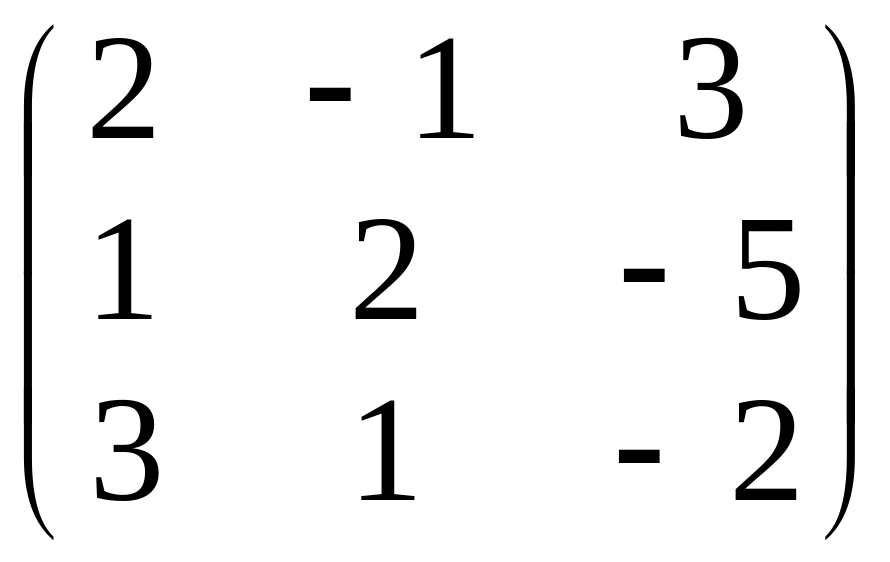

 получим
получим
![]() умножим
1-е уравнение на 2 и сложим, получим х,
затем 2-е уравнение умножим на (-2) и снова
сложим, найдем у.
Получим:
умножим
1-е уравнение на 2 и сложим, получим х,
затем 2-е уравнение умножим на (-2) и снова
сложим, найдем у.
Получим:
![]() или
или
![]() .
Задавая различные значения z
получим множество решений х
и у.
.
Задавая различные значения z
получим множество решений х
и у.
3. Понятие линейного пространства.
Мы с вами встречали множества, в которых были определены операции сложения и умножения на число. Например: сумма матриц, умножение матрицы на число. Существуют и другие множества, например, множество векторов.
В каждом множестве операции определяются по–своему. Например: вектора складываются по правилу параллелограмма, но разные по природе множества имеют одни и те же свойства, коммутативность и ассоциативность сложения и т.д.
В связи с этим возникает необходимость, исследовать множество, состоящее из элементов, какой – угодно природы, в котором определены операции сложения двух элементов и умножения на число. Сами операции, могут быть определены каким – угодно способом, лишь бы они обладали определенным набором свойств.
Опр.: Множество L называется линейным пространством, а его элементы векторами, если:
задан закон (операция сложения) по которому элементам
 и
и
 сопоставляется элемент
сопоставляется элемент
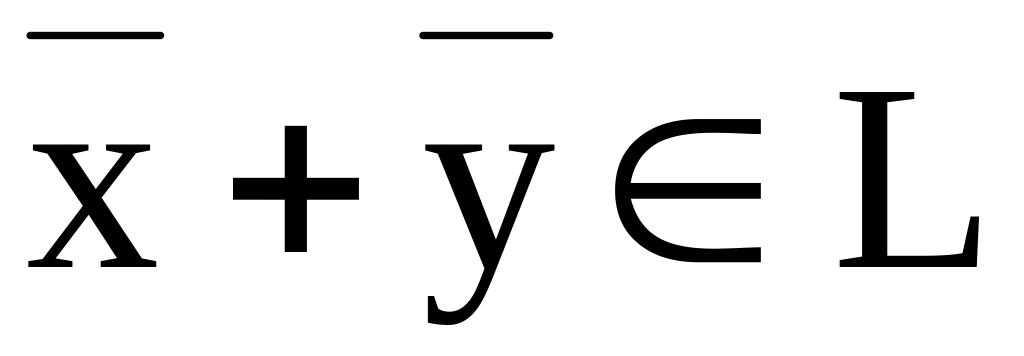 ,
называемый суммой.
,
называемый суммой.задан закон (операция умножения на число) по которому элементу
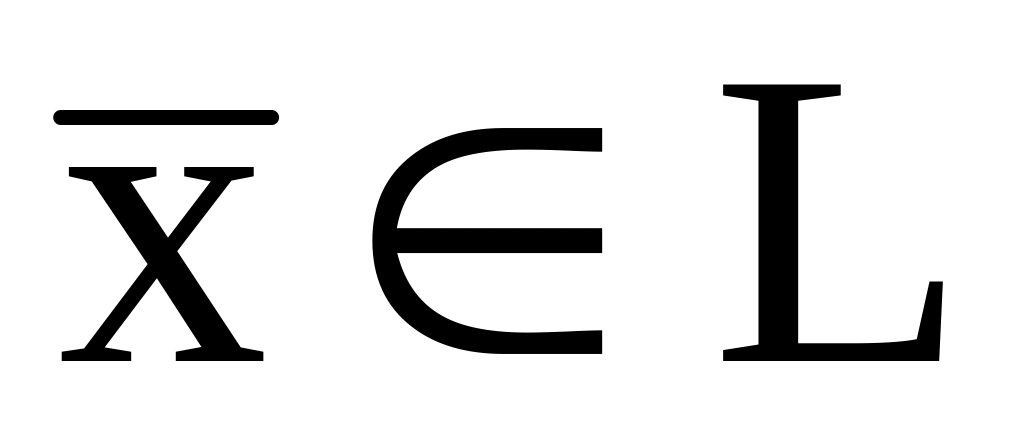 и числу
сопоставляется элемент
и числу
сопоставляется элемент
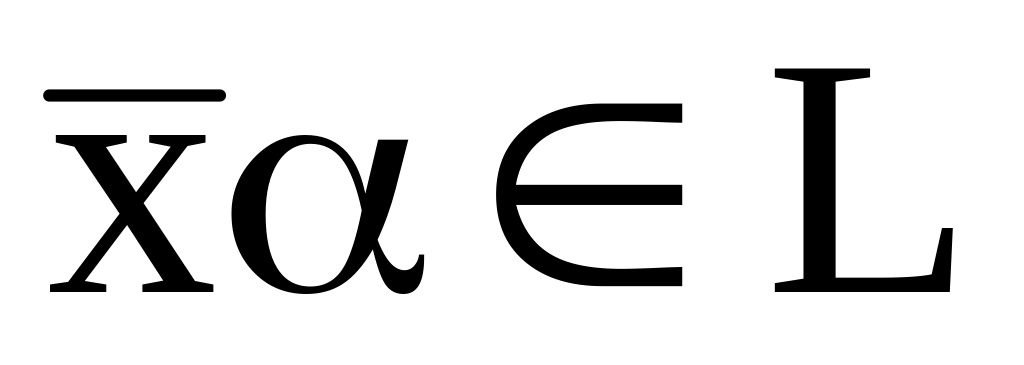 .
.
Обе
операции обладают следующими свойствами:
для любых
![]() ,
,
![]() ,
,
![]() и чисел
и
выполняются следующие аксиомы:
и чисел
и
выполняются следующие аксиомы:


 элемент
0=(0,…0) такой, что для
элемент
0=(0,…0) такой, что для
 выполняется
выполняется
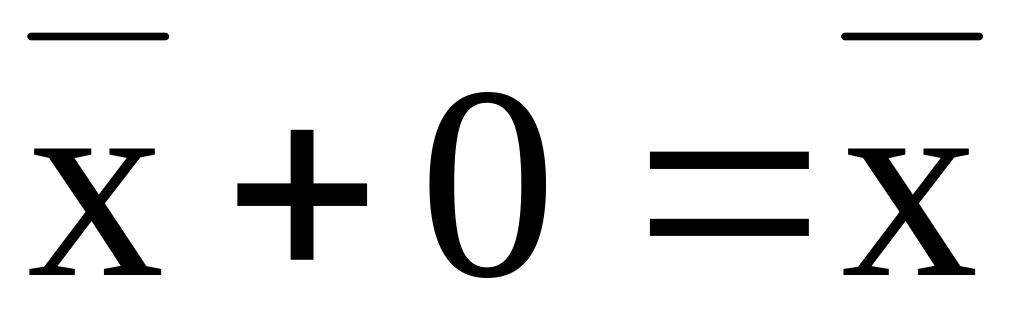 ,
и он называется нуль вектором.
,
и он называется нуль вектором.Для
 -
-
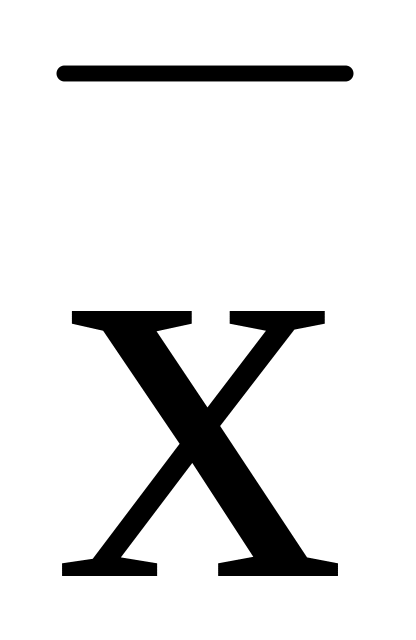 ,
такой что
,
такой что



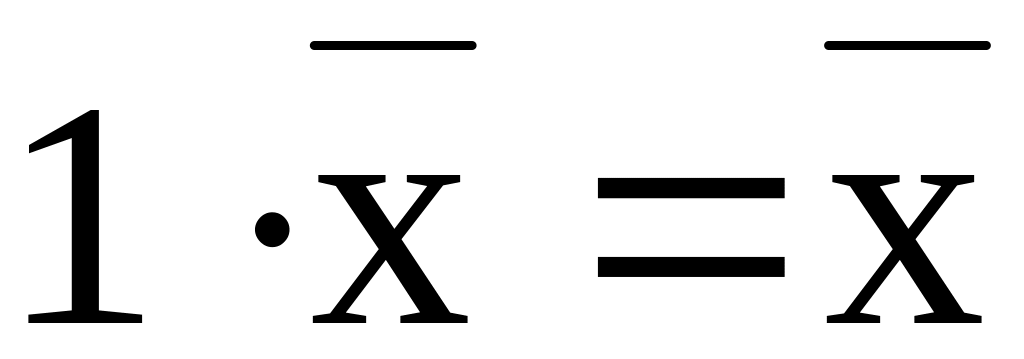
Опр.: Совокупность векторов пространства является замкнутой относительно операции сложения и умножения на число в том смысле, что в результате этих операций получается новый вектор принадлежащий этой совокупности.
Опр.:
(линейной независимости векторов).
Векторы
![]() ,
,
![]() называются линейно независимыми, если
их линейная комбинация равна нулю, при
условии, что все i=0.
называются линейно независимыми, если
их линейная комбинация равна нулю, при
условии, что все i=0.
![]()
![]()
![]()
Опр.: Размерностью линейного пространства называется наибольшее число, имеющихся в нем линейно - независимых векторов (d(L), dim L).
Опр.: Линейное (векторное) пространство называется n – мерным, если в нем можно найти n – линейно – независимых векторов.
Опр.: Пространство, имеющее конечную размерность, называется конечно – мерным. Размерность нулевого пространства равна нулю.
