5. Ідеальний газ у молекулярно-кінетичній теорії

Ідеальний газ. У розрідженого газу відстані між молекулами в багато разів перевищують їхні розміри. У цьому випадку взаємодія між молекулами таке маленьке, що їм можна зневажити, і кінетична енергія молекул набагато більше потенційної енергії взаємодії. Молекули газу можна розглядати як дуже маленькі тверді кульки. Притягання між молекулами (кульками) ні, а сили відштовхування виявляються лише в мізерно маленькі інтервали часу при зіткненнях молекул одна з однієї.

Замість реального газу, між молекулами якого діють складні сили взаємодії, ми будемо розглядати його фізичну модель. Ця модель називається ідеальним газом. Ідеальний газ — це газ, взаємодія між молекулами якого така маленька, що нею можна знехтувати.

6. Основне рівняння молекулярно-кінетичної теорії газів

Нехай газ утримується в прямокутній посудині одна зі стінок якої е поршень , здатний переміщатися без тертя. Причому газ і посудину мають однакові температури.

Обчислимо тиск газу на поршень . Поверхня поршня розміщена перпендикулярно до осі Ox. Тиск газу виникає внаслідок зіткнень молекул з поршнем. Щоб поршень не був виштовхнутий з посудини, до нього ззовні треба прикласти деяку силу F

Висновок формули для тиску газу не дуже складне, але досить громіздке. Поділимо його на чотири етапи. Спочатку обчислимо імпульс сили, що діє на поршень із боку однієї молекули під час зіткнення. Потім обчислимо кількість зіткнень молекул з поршнем за час t. Перемноживши ці величини й взявши середнє значення квадрата швидкості молекул, знайдемо імпульс середньої сили, що діє на поршень із боку всіх молекул. На останньому етапі поділимо добуту величину на час ∆t і площа поршня. У результаті одержимо вираження для тиску газу.

Зіткнення молекули з поршнем. Спочатку розглянемо випадок, коли швидкість V₀ молекули до зіткнення з поршнем перпендикулярна до поверхні поршня. Молекули в нашій моделі — це тверді кульки. Зіштовхуючись зі стінкою, вони відскакують від її без зміни кінетичної енергії. Подібні зіткнення називають абсолютно пружними. При цьому модуль швидкості не змінюється, а напрямок руху змінюється на протилежний: . Зміна імпульсу молекули рівняється:

.

А якщо швидкість молекули спрямована під довільним кутом до поршня, то під час зіткнення молекули з поршнем проекція υ_0x її швидкості на напрямок, перпендикулярне до поверхні поршня, змінює знак υ_x = - υ_0x,, а проекції υ_0y й υ_0z швидкостей на напрямки, паралельні поверхні поршня, залишаються без зміни: υ_y= υ_0y, υ_z= υ_0z. Одне й тим же відбувається з м'ячем під час зіткнення із гладенькою стінкою, якщо вважати це зіткнення абсолютно пружним.

Зміна проекції імпульсу молекули на вісь Ox рівняється:

За законом збереження імпульсу сумарний імпульс молекули й поршня залишається незмінним. Це означає, що модуль зміни імпульсу поршня рівняється модулю зміни імпульсу молекули. Інакше кажучи, під час зіткнення молекули з поршнем поршню передається імпульс, модуль якого рівняється 2m₀ |υ_X| .Напрям векторів швидкостей до та після удару о стінку та проекції векторів на осі координат розглянути на рис.3.

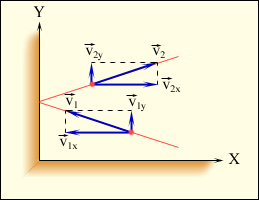
Рис.3. Напрям векторів швидкості до та після удару

Відповідно до другого закону Ньютона зміна імпульсу тіла рівняється імпульсу сили — добутку сили на час його дії. Тому модуль імпульсу сили, що діє на поршень із боку молекули за час удару, рівняється 2m₀ |υ_X|

Кількість зіткнень молекул з поршнем. Щоб обчислити імпульс сили, що діє на поршень із боку молекул, потрібно підрахувати кількість зіткнень молекул з поршнем за деякий інтервал часу ∆t, набагато більший за час зіткнення з поршнем однієї молекули.

За час ∆t поршня можуть досягти лише молекули, які перебувають від нього на відстані, що не перевищує |v_x|∆t. Молекули, які перебувають на більших відстанях, не встигають долетіти до поршня.

Значення проекцій швидкостей υ_Y й υ_Z не впливають на досягнення молекулами поршня .

Виділений об'єм рівняється |v_x|∆t* S ( рис.4).Якщо концентрація молекул, тобто кількість молекул в одиниці об'єму, становить , то кількість їх у виділеному об'ємі рівняється n|v_x|∆t*S.

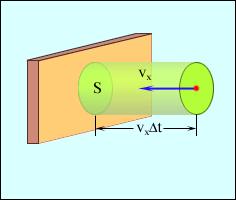
Рис.4. Виділений об’єм для розрахунку кількості зіткнень

Внаслідок хаотичності руху в середньому лише половина молекул у виділеному об'ємі має проекцію швидкості v_x > 0 і рухається ліворуч праворуч. У другої половини молекул v_x < 0, і вони рухаються в протилежному напрямку.

Отже, за час ∆t кількість ударів z молекул об поршень, що рівняється половині всіх молекул у виділеному об'ємі, становить

Імпульс середньої сили, що діє на поршень із боку всіх молекул. Кожна молекула під час зіткнення змінює імпульс поршня на 2m₀ |υ_X|. За час ∆t всі z молекул змінять його імпульс на 2m₀ |υ_X|z. Відповідно до другого закону Ньютона модуль F∆t імпульсу сили, що діє на поршень, рівняється модулю зміни його імпульсу:

Тепер треба врахувати таке: міркування велися так, начебто швидкість всіх молекул однакова. Насправді швидкості молекул різні, і кожна з них, ударяючись об поршень, вносить свій особливий внесок у тиск. Щоб урахувати це, треба взяти середнє по всіх молекулах значення квадрата проекції швидкості замість .

Вираз для середнього значення модуля імпульсу сили визначиться формулою . Оскільки , те

Тиск газу. Поділивши ліву й праву частини рівняння па добуток ∆t*S, визначимо тиск газу:

Це і є основне рівняння кінетичної-молекулярно-кінетичної теорії.

Якщо через позначити середню кінетичну енергію поступального руху молекули , то рівняння можна записати у вигляді:

Р=

Тиск ідеального газу пропорційний добутку кількості молекул в одиниці об'єму на середню кінетичну енергію поступального руху молекули.