1.10. Формулы полной вероятности и Байеса

Предположим, что с данным случайным экспериментом связана полная группа событий , вероятности которых известны. Нас интересует некоторое событие А, которое может наступить одновременно с одним из . При этом условные вероятности наступления события А при каждом известны. Требуется определить безусловную вероятность .

Представим событие А в виде:

.

В полученной сумме слагаемые являются попарно несовместными: , . Поэтому, используя аксиому аддитивности и правило умножения вероятностей, получаем:

.

Формула

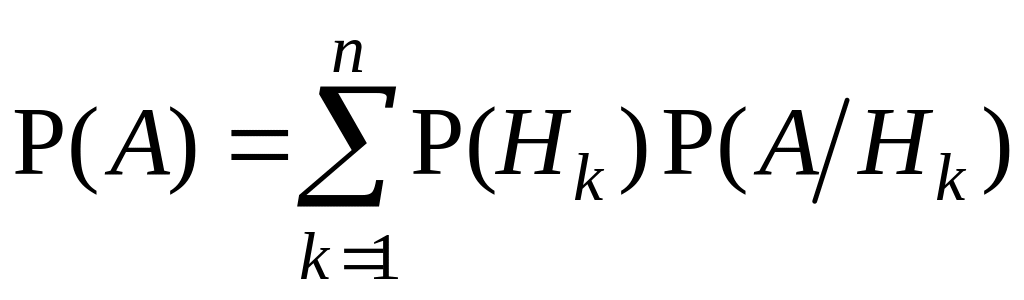
называется формулой полной вероятности. В ней события называются гипотезами (так как одно из обязательно происходит), а вероятности - вероятностями гипотез.

Пусть, по-прежнему, со случайным экспериментом связано n гипотез , вероятности которых известны. Известно также, что гипотеза сообщает событию А вероятность . Предположим, что эксперимент был произведён, и в результате событие А произошло. Этот факт приводит к переоценке вероятностей гипотез . Количественно этот вопрос решает следующая формула:

.

Полученная формула называется формулой Байеса (или формулой гипотез). В ней называются априорными вероятностями гипотез (они определяются a priori – до проведения опыта). Условные вероятности называются апостериорными вероятностями гипотез (они вычисляются a posteriori – после проведения опыта, когда стало известно, что событие А произошло).

Пример. По каналу связи с помехами передаются двоичные символы {0,1}. Вероятности искажения символов в канале (0 1, 1 0) одинаковы и равны 0.2. Вероятность символа 0 на входе канала равна 0,9, а вероятность символа 1 - 0,1. На выходе канала принят сигнал, соответствующий 1. Определить вероятность того, что на вход канала подавалась также 1.

Решение.

Рассмотрим гипотезы

= {На входе канала связи символ 0},

= {На входе канала связи символ 1}.

Очевидно, и по условию , то есть события и образуют полную группу событий.

Пусть событие А = {На выходе канала принят символ 1}.

Тогда по условию задачи вероятность искажения символа 0 в канале суть условная вероятность , а условная вероятность является вероятностью неискажения в канале символа 1. В терминах введенных обозначений требуется найти условную (апостериорную) вероятность .

Найдем вначале по формуле полной вероятности безусловную вероятность события А:

.

Затем, в соответствии с формулой Байеса, находим апостериорную вероятность :

(при априорной вероятности ).

Очевидно, что при этом апостериорная вероятность

(при априорной вероятности ).

Замечание. Таким образом, даже при приеме на выходе канала связи 1 мы отдаем предпочтение в пользу 0 на входе. Это объясняется тем, что априорная вероятность 0 на входе канала существенно больше априорной вероятности 1.

1.11. Схема независимых испытаний Бернулли

Предположим, что некоторый эксперимент может повторяться при неизменных условиях сколько угодно раз, и эти повторения не зависят друг от друга. В этом случае говорят о проведении последовательности независимых испытаний. Независимость испытаний при этом следует понимать в том смысле, что любые события, которые могут произойти в результате, являются независимыми в совокупности.

Простейшей является последовательность независимых испытаний, в каждом из которых возможно только 2 исхода: успех – У (1) и неуспех – Н (0). Последовательность независимых испытаний с двумя исходами называется схемой независимых испытаний Бернулли.

Обозначим вероятность успеха , а вероятность неуспеха .

При проведении n независимых испытаний по схеме Бернулли пространство элементарных событий имеет вид:

,

а вероятности элементарных событий в силу независимости вычисляются по формуле:

,

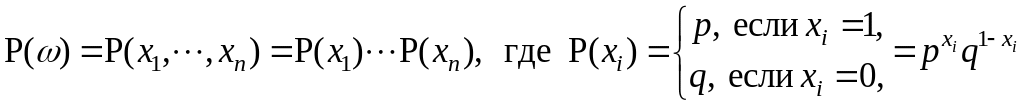то есть

.

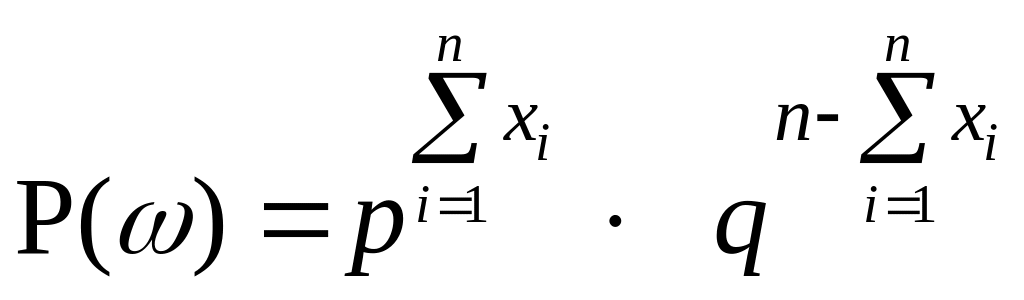В связи с рассмотрением схемы независимых испытаний Бернулли обычно представляют интерес события

={В n испытаниях наступило ровно m успехов} = = .

Обозначим вероятность и вычислим ее. Для любого вероятность , а общее количество исходов, содержащихся в , равно числу способов размещения m единиц в последовательности длины n из нулей и единиц, то есть . Таким образом,

.

Полученная формула называется формулой Бернулли. Она даёт выражение для вероятности наступления m успехов в n независимых испытаниях по схеме Бернулли с неизменной вероятностью успеха в одном испытании равной p и с вероятностью неуспеха равной q = 1 – p.

Поскольку события образуют полную группу событий, то . Тот же результат можно получить и на основании бинома Ньютона:

Исследуем поведение вероятностей в зависимости от m. Для этого вычислим отношение:

.

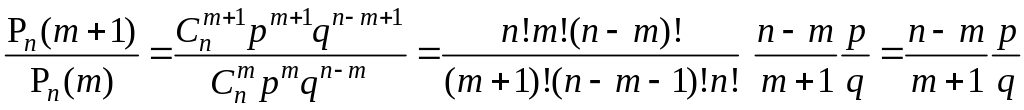Отсюда следует, что вероятности возрастают, когда 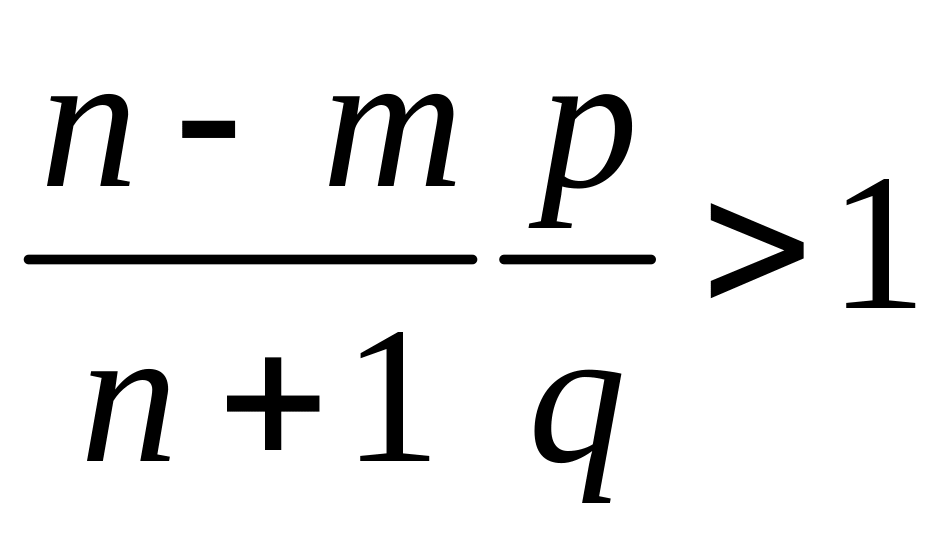или, что эквивалентно, .

Вероятности убывают, когда 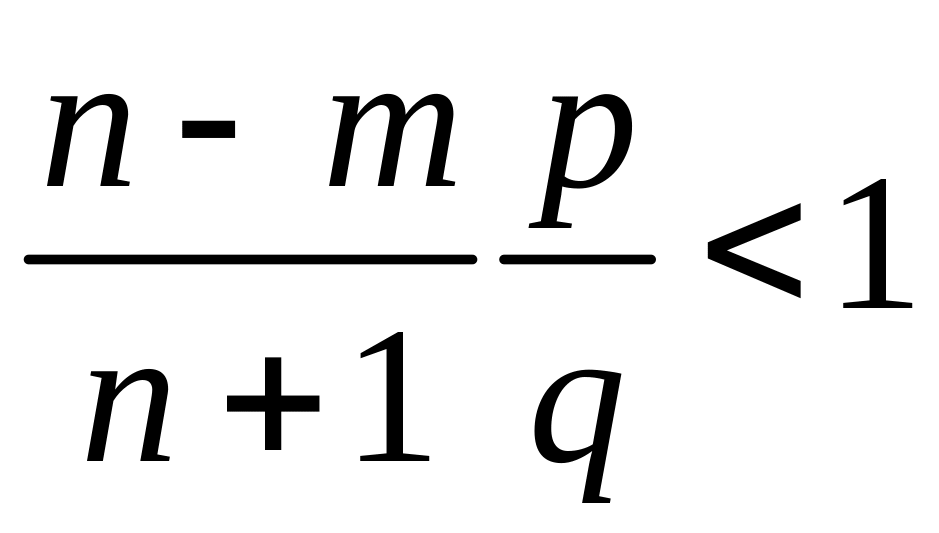или, что эквивалентно, .

И, наконец, , если .

Определение. Число успехов m = m₀, при котором вероятности достигают максимума, называются наивероятнейшим числом успехов.

Из проведённых рассуждений следует, что наивероятнейшее число успехов m₀ определяется из двойного неравенства:

.

При этом:

1. Если число 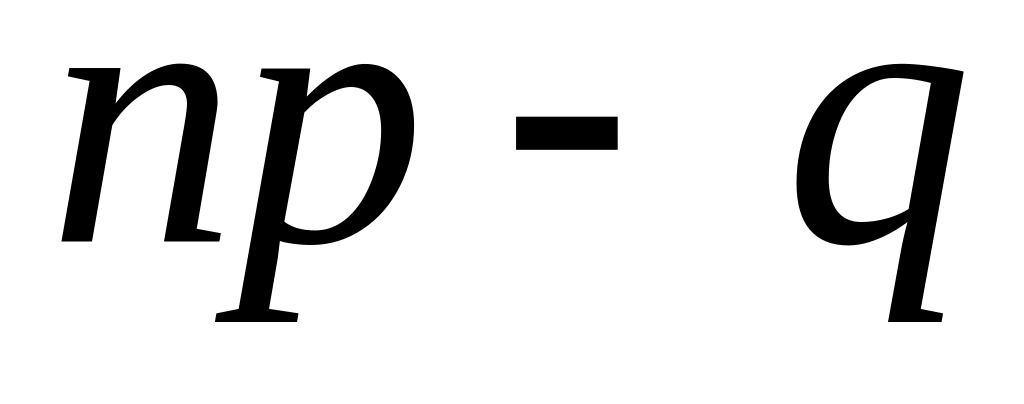нецелое, то существует одно наивероятнейшее число успехов: .

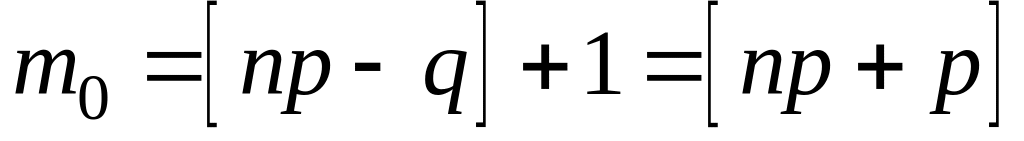2. Если число целое, то существует два наивероятнейших числа успехов: 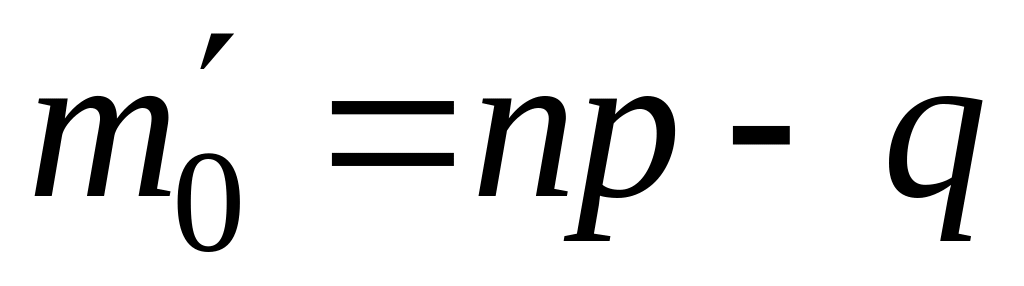и .

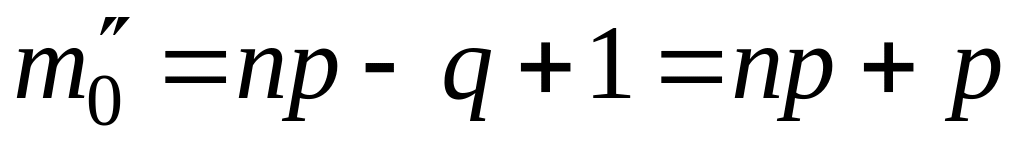3. Если число целое, то .

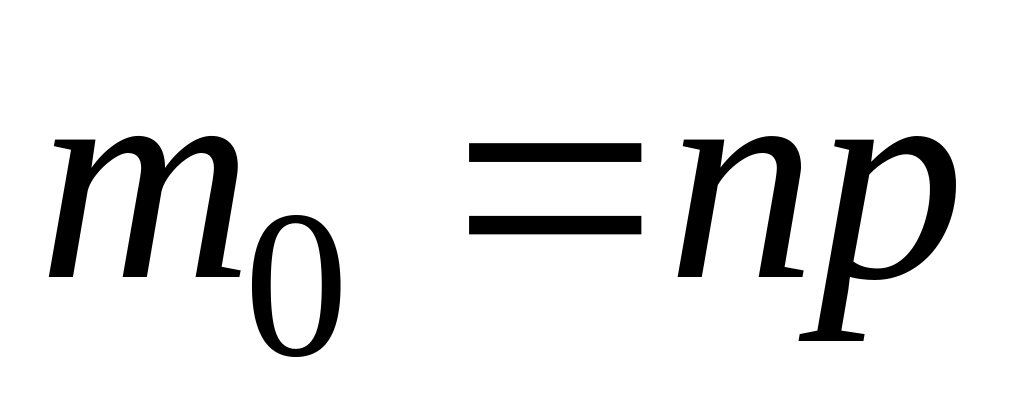Вычисления по формуле Бернулли при больших m и n весьма трудоёмкие. На практике в этом случае используют асимптотические приближения для вероятностей , основанные на предельных теоремах Пуассона и Муавра-Лапласа.

Пример.

Что более вероятно: выиграть у равносильного противника 3 партии из 4 или 5 из 8 (ничьи не считаются)?

Решение.

В данном примере речь идет о сравнении двух вероятностей и , когда . Поскольку , а , то , то есть выиграть 3 партии из 4 более вероятно.

30