Свойства операций над событиями
Приступим теперь к введению понятия вероятности. Делать мы это будем постепенно, как бы повторяя исторический путь. Такой подход позволяет избежать формального восприятия и способствует развитию теоретико-вероятностной интуиции. Начнем с, так называемого, классического определения вероятности.
1.4. Классическое определение вероятности
На самом деле это не определение, а метод вычисления вероятностей событий во вполне определенных и сильно ограниченных условиях.
Говорят, что случайный эксперимент удовлетворяет классическому определению вероятности (или классической вероятностной схеме), если:
пространство элементарных событий состоит из конечного числа исходов
;
из соображений симметрии можно считать, что все элементарные исходы эксперимента являются равновозможными (т. е. ни один из исходов не имеет предпочтения перед другими).
Согласно классическому
определению вероятности вероятность
любого события
,
равна отношению числа
исходов, благоприятствующих
событию
,
к общему числу исходов
:
Свойства вероятности, непосредственно вытекающие из классического определения вероятности:
1°.
для любого события А
(доказательство
очевидно).
2°.
(доказательство
очевидно).
3°. Если события
и
несовместны
,
то
.
▲ Пусть событию
А благоприятствует
исходов, а событию В
-
исходов. Поскольку события А
и В
являются несовместными (т.е. не имеют
общих исходов), то сумме
благоприятствует
исходов. Поэтому
.■
Исходя из свойств 1 3 (и только!!!) вытекают также следующие свойства вероятности:
4°.
.
▲ Поскольку события
образуют полную группу событий (
),
то из свойств 2° и 3°
.■
5°.
.
▲ Следует из
свойств 2° и 4°, поскольку события
.■
6°.
.
▲ Представим
событие В
в виде:
.
Поскольку события
являются несовместными, то из свойств
1° и 3° имеем:
.■
7°.
.
▲ Следует из
свойств 2°, 5° и 6°, так как
(в частности, свойство 7° означает, что
измерять вероятность в процентах
некорректно).■
При решении задач с использованием классического определения вероятности, широко используются понятия комбинаторики. Напомним некоторые из них.
Размещением
из N
элементов некоторого множества по M
элементов называется любой упорядоченный
набор из M
элементов данного множества. Число всех
размещений равно
.
Если в упорядоченном
наборе элементы могут повторяться, то
этот набор называется размещением
с повторениями.
Число размещений с повторениями: равно
.
Перестановкой
из N
элементов некоторого множества называется
размещение из N
элементов по N.
Число всех перестановок равно
.
Сочетанием из
N
элементов некоторого множества по M
элементов называется любое подмножество
мощности M.
Число всех сочетаний равно
.
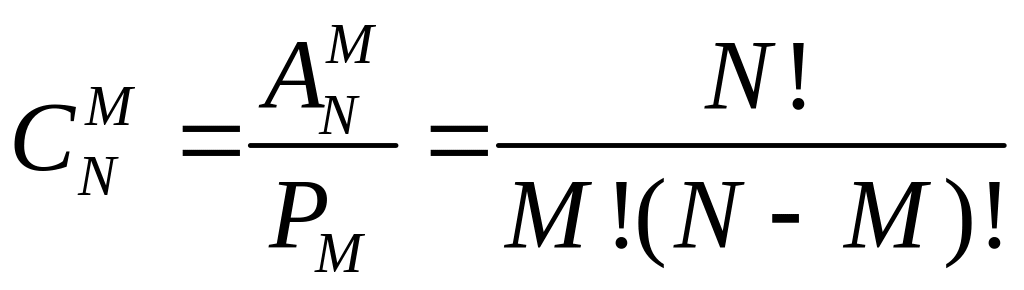Пример 1.
Определить вероятность события А, заключающегося в том, что при бросании двух игральных костей, сумма очков не превысит 4.
Решение. В данном
примере важно понимать, что если в
качестве исхода эксперимента понимать
значение суммы выпавших очков:
или количество очков, выпавших на каждой
из костей без учета порядка их следования:
,
то исходы не являются равновозможными
и классическое определение вероятности
не применимо. Верное решение в соответствии
с классическим определением вероятности
можно получить, если только под исходом
понимать количество очков, выпавших на
каждой из костей с учетом порядка их
следования:
.
В этом случае
,
а
.
Поэтому
.
Пример 2 (Урновая схема).
В урне находится N шаров, из которых M белые. Из урны наугад извлекается n шаров. Какова вероятность того, что среди выбранных шаров окажется ровно m белых.
Решение. Исходами
в данном эксперименте являются любые
подмножества, содержащие n
шаров, и они являются равновозможными
(за счет слова «наугад»). Число всех
исходов равно числу сочетаний из n
по N:
.
Каждый набор шаров, входящий в интересующее
нас событие, состоит из m
белых шаров, которые можно выбрать из
M
белых
способами. Независимо от выбора белых
шаров, небелые шары можно выбрать
способами. Поэтому общее число
благоприятных исходов равно
.
Из этого следует, что
.
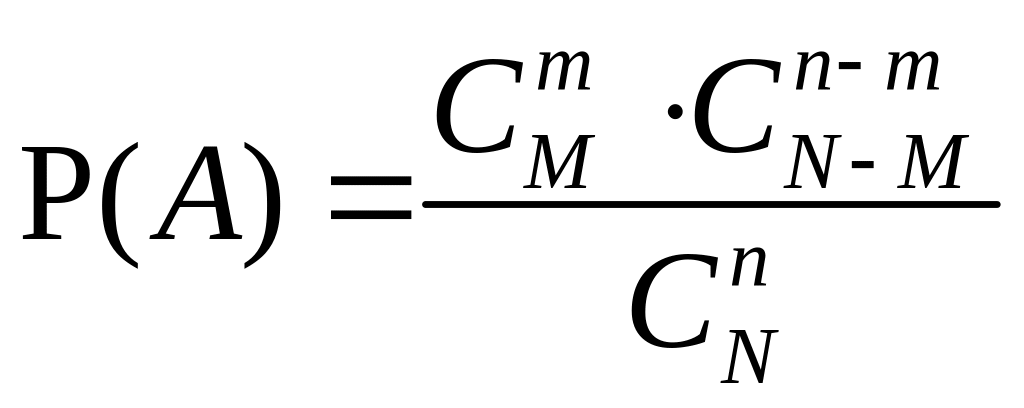