
- •Частина іі Математична статистика
- •Розділ іv. Статистична перевірка гіпотез
- •1.1 Статистичний розподіл вибірки
- •1.2 Емпірична функція розподілу
- •1.3 Полігон та гістограма
- •Приклад 3. Вибірку задано у вигляді розподілу частот
- •1.4 Тренувальні вправи
- •2.1 Точкові оцінки параметрів розподілу
- •Основні властивості вибіркової середньої
- •1) При множенні усіх варіант вибірки на однаковий множник вибіркова середня також множиться на цей множник:
- •Приклад 1. Вибіркова сукупність задана таблицею
- •2.2 Інтервальні оцінки параметрів розподілу
- •2.3 Тренувальні вправи
- •2.4 Обчислення параметрів розподілу методом добутків
- •2.5 Індивідуальне семестрове завдання №1 “Статистичний розподіл вибірки. Обчислення параметрів розподілу методом добутків”
- •2.6 Зразок виконання індивідуального семестрового завдання №1
- •2.7 Обробка вибірки методом найменших квадратів
- •2.8 Тренувальні вправи
- •2.9 Індивідуальне семестрове завдання №2 «Метод найменших квадратів»
- •2.10 Зразок виконання індивідуального семестрового завдання №2
- •Розділ ііі. Елементи теорії кореляції
- •3.2 Лінійна кореляція
- •3.3 Криволінійна кореляція
- •3.4 Рангова кореляція. Вибірковий коефіцієнт рангової кореляції Спірмена
- •3.5 Тренувальні вправи
- •3.6 Індивідуальне семестрове завдання №3 “Знаходження вибіркового коефіцієнта кореляції та прямих ліній регресії”
- •Варіант 5. Розподіл 50 за вартістю основних виробничих фондів (млн. Грн) та витратами (% до вартості основних фондів) на капітальний ремонт дано у таблиці:
- •Варіант 6. Розподіл 40 заводів кольорової металургії за середньодобовим виробленням металу (тис.Т) та затратами електроенергії на 1 тн. (тис. КВт-год) дано у таблиці:
- •Варіант 7. Розподіл 80 корів за живою вагою (кг) та надоями молока (кг) дано у таблиці:
- •Варіант 8. Розподіл 100 ткацьких фабрик за виробничими потужностями (тис. М. На рік) та собівартістю 1 м тканини (грн) дано у таблиці:
- •Варіант 9. Розподіл 100 прямокутних чавунних плиток за довжиною (см) та масою (кг) дано у таблиці:
- •Варіант 10. Розподіл 200 заводів за вартістю основних фондів (млн. Грн.) та вартістю готової продукції ( млн. Грн.) дано у таблиці:
- •Варіант 11. Розподіл підприємств за об’ємом продукції (грн) та за її собівартістю (грн) надано у таблиці:
- •Варіант 12. Розподіл 120 вагонних коліс за терміном служби (в роках) та величиною зносу ободу колеса (в мм) дано у таблиці:
- •Варіант 14. Розподіл 100 проб руди з вмістом окису заліза (%) та закису заліза (%) дано у таблиці:
- •Варіант 15. Розподіл однотипних підприємств за вартістю основних фондів (млн. Грн) та собівартістю одиниці продукції (грн) дано у таблиці:
- •Варіант 16. Розподіл 100 прямокутних плиток за їх довжиною (см) та масою (кг) дано у таблиці:
- •За відповідним рівнянням регресії оцінити середнє значення собівартості вугілля тих шахт, глибина виробок яких складає 800 м, та порівняти одержаний результат з відповідним груповим середнім.
- •За відповідним рівнянням регресії оцінити середнє значення газоносності тих шахт, глибина виробок яких складає 900 м, та порівняти його з відповідним груповим середнім.
- •3.7 Зразок виконання індивідуального семестрового завдання №3 Розподіл однотипних підприємств за вартістю основних фондів (млн. Грн) та собівартістю одиниці продукції (грн) дано у таблиці:
- •3.8 Питання для самоперевірки
- •Розділ іv. Статистична перевірка гіпотез
- •4.1 Поняття статистичної гіпотези
- •4.2 Критична область. Знаходження критичних областей
- •4.3 Критерій узгодження Пірсона
- •4.4 Тренувальні вправи
- •4.5 Питання для самоперевірки
- •Література
- •Додатки Додаток а Таблиця значень функції (х)
- •Додаток б
- •Додаток в
- •Додаток д
- •Додаток е Критичні точки розподілу 2
- •Додаток ж Критичні точки розподілу Стьюдента
- •Додаток и Критичні точки розподілу f Фішера – Снедекора
- •Додаток к Критичні точки розподілу Колмогорова
4.2 Критична область. Знаходження критичних областей
Після обрання певного критерію узгодження, множину усіх його можливих значень поділяють на дві підмножини, що не перетинаються: одна з них містить значення критерію, при яких основна гіпотеза відхиляється, а друга – при яких вона приймається.
Критичною областю називають сукупність значень критерію, при яких основна гіпотеза відхиляється.
Областю прийняття гіпотези (областю допустимих значень) називають множину значень критерію, при яких гіпотезу приймають.
Критерій узгодження К - одновимірна випадкова величина, усі її можливі значення належать деякому інтервалу. Тому критична область та область прийняття гіпотези також будуть інтервалами, а це означає, що існують точки, які ці інтервали відокремлюють.
Критичними
точками
(межами)
критерію К
називають точки
![]() ,
які відокремлюють критичну область від
області прийняття гіпотези.
,
які відокремлюють критичну область від
області прийняття гіпотези.
Розрізняють однобічну (правобічну та лівобічну) та двобічну критичні області.
Правобічною називають критичну область, що визначається нерівністю К > , де – додатне число.
Лівобічною називають критичну область, що визначається нерівністю К < , де – від’ємне число.
Щоб знайти однобічну критичну область, треба знайти критичну точку . Для цього задають достатньо малу ймовірність – рівень значущості , а потім шукають критичну точку з врахуванням вимоги
![]()
у випадку правобічної критичної області, або
![]()
у випадку лівобічної критичної області.
У випадку двобічної критичної області повинно виконуватись тотожність
![]() .
.
Для кожного критерію узгодження є відповідні таблиці (наприклад, таблиці додатка), які дозволяють знайти таку точку , яка задовольняє потрібну умову.
При визначенні критичної області доцільно враховувати потужність критерію.
Потужністю критерію називають імовірність належності критерію критичної області при умові, що правильна альтернативна гіпотеза.
Іншими словами, потужність критерію є імовірність того, що основна гіпотеза буде відхилена, якщо альтернативна гіпотеза правильна.
Якщо рівень значущості вже обрано, то критичну область доцільно будувати так, щоб потужність критерію була максимальною. Виконання цієї вимоги забезпечую мінімальну імовірність похибки другого роду.
Єдиний засіб одночасного зменшення ймовірностей похибок першого та другого роду – це є збільшення об’єму вибірки.
Порядок дій при перевірці гіпотез
Для
перевірки правильності основної
статистичної гіпотези
![]() необхідно:
необхідно:
1)
визначити гіпотезу
![]() ,
альтернативну до гіпотези
;
,
альтернативну до гіпотези
;
2) обрати статистичну характеристику перевірки;
3) визначити допустиму імовірність похибки першого роду, тобто рівень значущості ;
4) знайти за відповідною таблицею критичну область (критичну точку) для обраної статистичної характеристики.
До критичної області належать такі значення статистичної характеристики, при яких гіпотеза відхиляється на користь альтернативної гіпотези .
Підкреслимо, що між рівнем значущості та критичною областю існує такий зв’язок: якщо гіпотеза правильна, то з імовірністю значення вибіркової функції будуть належати критичній області.
Так, при перевірці гіпотези про рівність дисперсій двох нормальних сукупностей при альтернативній
![]()
треба знайти спостережне значення критерію Фішера-Снедекора, тобто
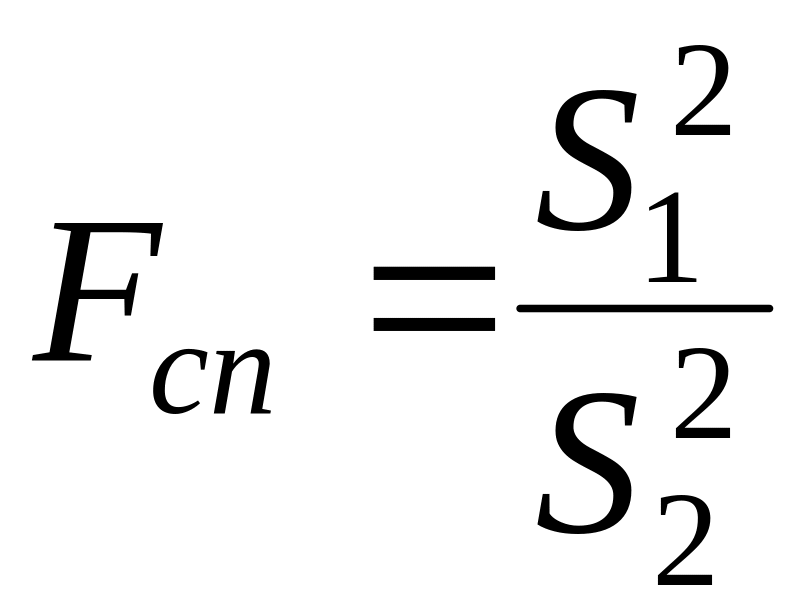 ,
,
а
потім з таблиці критичних точок цього
розподілу за заданим рівнем значущості
та степенях вільності
![]() та
та
![]() знайти
знайти
![]() .
.
Якщо
![]() ,
то гіпотеза
приймається.
,
то гіпотеза
приймається.
Якщо
![]() ,
то гіпотезу
відхиляють.
,
то гіпотезу
відхиляють.
