2.7 Обробка вибірки методом найменших квадратів

Оцінка параметрів лінійної функції

При експериментальному вивченні функціональної залежності однієї величини Y від іншої величини Х роблять ряд вимірів величини у при різних значеннях х. Результати можуть бути представлені у вигляді таблиці:

			…		…
			…		…

Метод, заснований на вимозі мінімізації суми квадратів відхилень, називається методом найменших квадратів.

З його допомогою зображують статистичну функціональну залежність у вигляді аналітичної залежності й виражаються такі оцінки параметрів рівняння регресії, які зводять до мінімуму обрану міру розкиду.

У результаті відбувається вирівнювання емпіричних значень в одну лінію регресії.

При цьому, для однозначного визначення як міру розкиду використовують один з показників розсіювання випадкової величини – дисперсію.

Припустимо, що діаграма розсіювання така, що між величинами х и у існує лінійна залежність

,

де параметри а та невідомі.

Це означає, що відхилення фактичних значень функції від «підібраної прямої» повинні бути мінімальними, тобто пряма підбирається так, щоб сума квадратів відхилень була мінімальною

.

Нехай – є рівняння « підібраної прямої».

Тоді повинна виконуватися рівність

.

Потрібно визначити параметри а й b так, щоб z досягло мінімуму.

Відомо, що необхідна умова існування мінімуму полягає в тому, що:

Після диференціювання і спрощень, одержимо систему рівнянь

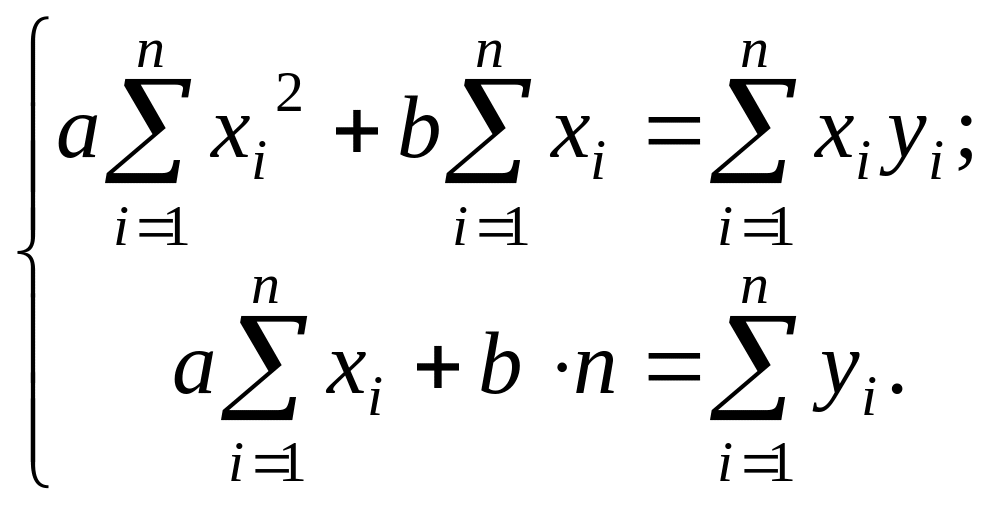
яка називається системою нормальних рівнянь у випадку вибору емпіричної функції у вигляді лінійної залежності.

Приклад 1. Методом найменших квадратів знайти значення параметрів емпіричної функції, якщо дослідницькі дані про значення х и у представлені в таблиці:

х	6	8	9	9	10	11	12	13	14	15
у	4	4	5	7	5	6	8	7	9	10

Розв’язання. За вибіркою спостережень побудуємо в системі координат х0у діаграму розсіювання, тобто побудуємо точки

.

Аналіз дослідницьких даних показує, що в якості емпіричної (підібраної) функції можна використати лінійну функцію

.

Для знаходження параметрів а й b застосуємо МНК.

Тоді для визначення параметрів а й b будемо мати систему нормальних рівнянь:

Для зручності обчислень складемо наступну розрахункову таблицю ( ):

1	6	4	36	24
2	8	4	64	32
3	9	5	81	45
4	9	7	81	63
5	10	5	100	50
6	11	6	121	66
7	12	8	144	96
8	13	7	169	91
9	14	9	196	126
10	15	10	225	150

Підставимо дані останнього рядка таблиці в нормальну систему рівнянь:

Розв’язавши систему, одержимо

.

Підставляючи ці значення параметрів, одержимо емпіричну функцію:

,

яка описує залежність між випадковими величинами х та у.

Оцінка параметрів параболічної функціональної залежності

Нехай між випадковими величинами та існує функціональна залежність вигляду

.

Методом найменших квадратів на основі даних випробувань знайдемо значення невідомих параметрів .

Тепер формула буде мати вигляд

.

Для цієї функції шуканими величинами є параметри , й тому, відповідно до вимог екстремуму функції, треба, щоб

.

Дифенціруючи, після спрощень, маємо систему

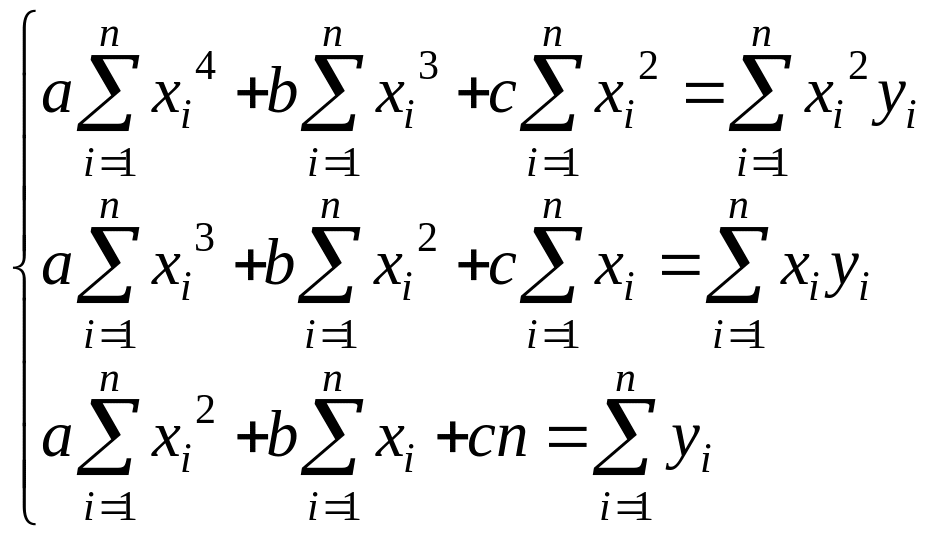
яка є системою нормальних рівнянь у випадку вибору квадратичної функції в якості емпіричної функції.

Складемо розрахункову таблицю:

1 2 ... ... п

Підставляючи дані останньої строчки в систему нормальних рівнянь і розв’язавши її любим з відомих методів, знайдемо значення параметрів .

Отже, матимемо рівняння квадратичної функції в якості емпіричної

.

Приклад 2. Застосовуючи метод найменших квадратів, скласти рівняння параболи , яка проходить найближче до точок

	0	1	2	3	4	5	6	7	8
	0,1	0,48	0,81	1,26	2,3	2,85	3,4	3,96	4,54

Розв’язання.

Для розв’язання системи нормальних рівнянь

(у випадку вибраної емпіричної функції – квадратичної) складемо розрахункову таблицю:

1	0	0,1	0	0	0	0	0
2	1	0,48	1	1	1	0,48	0,48
3	2	0,81	4	8	16	1,62	3,24
4	3	1,26	9	27	81	3,78	11,34
5	4	23	16	64	256	92	368
6	5	2,85	25	125	625	14,25	71,25
7	6	3,4	36	216	1296	20,4	122,4
8	7	3,96	49	343	2401	27,72	194,04
9	8	4,54	64	512	4096	36,32	290,56

Підставивши дані останньої строки у систему нормальних рівнянь, отримаємо

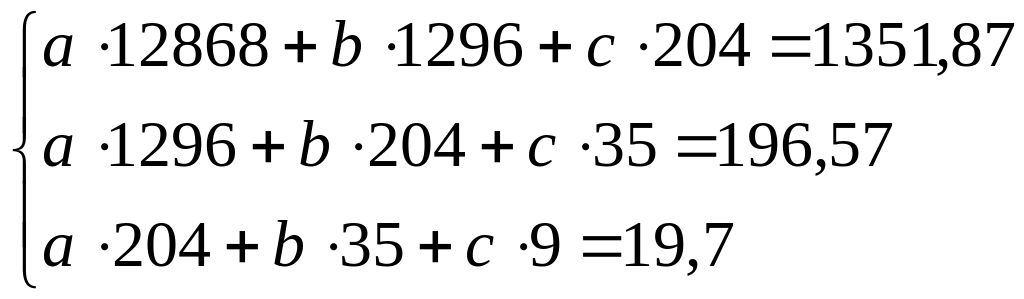
Розв’язуючи систему трьох невідомих будь-яким відомим методом, отримаємо значення

.

Таким чином, рівнянням шуканої параболи буде

.