1.1 Основні формули комбінаторики
Комбінаторика вивчає кількості комбінацій, підлеглим певним умовам, які можна скласти з елементів, байдуже якої природи, заданої кінцевої множини. При безпосередньому обчисленні ймовірностей часто використовують формули комбінаторики.
Приведемо найбільш важливі з них.
Нехай
дана множина
,
що
містить
елементів:
.
Розміщеннями
з
по
елементів
називаються сполуки, кожна з яких містить
різних елементів, взятих з даних
елементів, і які відрізняються одна від
одної або складом елементів, або їх
порядком.
Число
розміщень із
по
елементів
знаходиться за формулою:
Приклад
1.
.
Перестановками з елементів називаються сполуки, які складаються з різних елементів, і які відрізняються одна від одної лише порядком розміщення елементів.
Число перестановок із елементів .дорівнює добутку всіх натуральних чисел від 1 до :
.
Приклад 2 Скількома способами можна скласти список з 8 студентів ?
.
Комбінаціями з по елементів називаються сполуки, кожна з яких містить різних елементів, взятих з даних елементів і які відрізняються одна від одної хоча б одним елементом.
Число комбінації з по елементів знаходиться за формулою
Приклад 3. На зборах присутні 30 осіб. Скількома способами можна обрати президію зборів у складі трьох осіб?
Шуканим числом способів є число комбінацій з 30 по 3, тобто
.
Приклад 4. Скільки п’ятизначних чисел можна скласти із цифр 0, 1, 2, 3, 4, якщо кожна цифра входить до складу числа тільки один раз?
Розв’язання. Шукана кількість п’ятизначних чисел дорівнює різниці
.
Приклад 5. Скількома способами група з 16 студентів може обрати на конференцію делегацію з 4 осіб?
Розв’язання. Число можливих способів дорівнює
.
Приклад 6. У підрозділі 60 солдатів і 5 офіцерів. Скількома способами можна виділити караул, який складає 3 солдатів і одного офіцера?
Розв’язання. Трьох солдатів можна виділити:
.
способами.
Одного офіцера можна виділити:
способами.
Тоді за правилом добутку маємо:
.
1.2 Тренувальні вправи
1. Скількома способами можна вибрати з 10 кандидатів трьох людей на три різні посади?
.
2. З 10 кандидатів тренер відбирає п'ятьох і становить із них баскетбольну команду. Два кандидати можуть грати центровими, четверо - тільки в захисті, а інші - тільки в нападі. Скількома способами тренер може скласти команду?
Центрові
; захисники
;
нападаючі
.
За
правилом множення команда —
.
3. Скількома способами можна розташувати в ряд на книжковій полиці 5 різних книг?
.
4. Скількома способами можна вибрати й розташувати в ряд на книжковій полиці 3 з 5 різних книг?
.
5. Скільки існує телефонних номерів, що складаються з 5 різних цифр?
.
6. Скількома способами друг щодо друга можуть розміститися за столом 10 осіб?
.
7. У пасажирському поїзді 14 вагонів. Скількома способами можна розподілити по вагонах 14 провідників, якщо за кожним вагоном розподіляється один провідник?
.
8. Скількома способами можна вибрати чотирьох людей на чотири посади з 9 кандидатів на ці посади?
.
9. У команду з плавання повинні входити 4 юнака й 2 дівчини. Скількома способами можна скласти таку команду, якщо є 8 юнаків й 5 дівчат?
.
10. У групі 25 студентів, з них 11 відмінників. За списком відібрано 9 студентів. Скількома способами можна відібрати цих 9 студентів так, щоб серед них виявилося 5 відмінників?
.
11. Скількома способами можна вибрати 2 карандаші і 3 ручки з 5 різних карандашей та 5 різних ручок?
.
12. Скількома способами можна вибрати три різні фарби з наявних п'яти?
.
13. Скількома способами можна скласти триколірний смугастий прапор, якщо є матеріал 5 різних кольорів?
.
14. Обчислити:
.
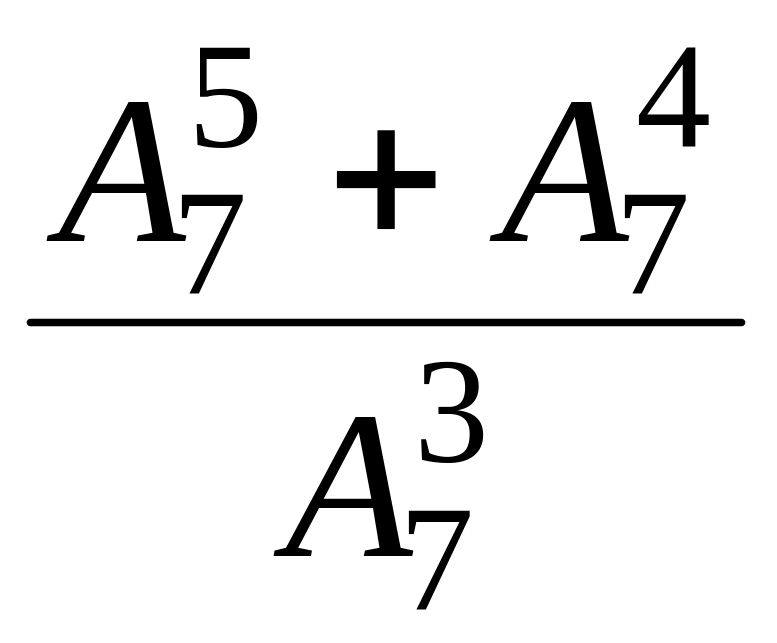16.
15.
Розв’язати рівняння:
.
.
16. У скількох точках перетинаються 10 прямих ліній, якщо між них немає паралельних прямих і через кожну точку перетинання проходять тільки дві прямі?
.
17. Скільки можна провести різних площин через 8 точок простору, якщо ніякі 4 з них не лежать в одній площині?
.
18.
Розв'язати
рівняння:
.
.
19.
Розв'язати
рівняння:
.
.
( скористатися формулою
).
20.
Розв'язати
рівняння:
.
.
21.
Розв'язати
рівняння:
.
.
22.
Розв'язати
рівняння:
.
.
23. Скільки може бути випадків при виборі 2 олівців й 3 ручок з 5 різних олівців й 5 різних ручок?
100.
24. Із групи 15 людей повинні бути виділені бригадир й 4 члени бригади. Скількома способами це можна зробити?
15015.
25.
Розв'язати
рівняння:
.
.
26.
Розв'язати
рівняння:
.
.
РОЗДІЛ ІІ. ВИПАДКОВІ ПОДІЇ ТА ЙМОВІРНОСТІ