Гіпергеометричний розподіл

Припустимо, що в партії з N виробів знаходяться M стандартних . З партії навмання відбирають п виробів. Визначимо через Х випадкову величину — число т стандартних виробів серед п відібраних.

Ймовірність того, що з п відібраних т стандартних знаходиться за формулою:

.

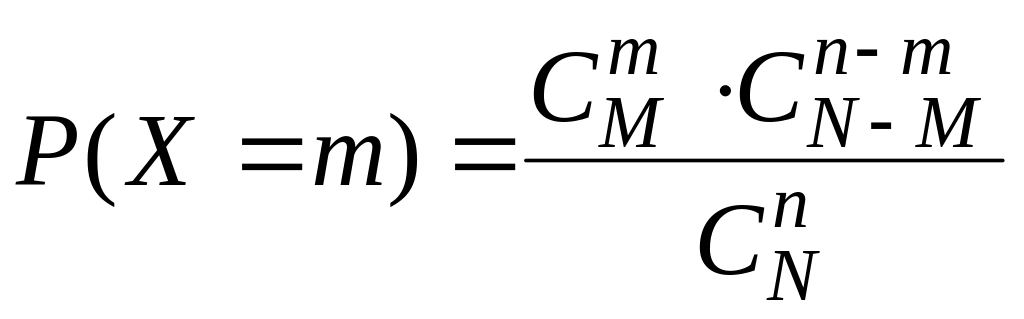Приклад 5. Серед 50 виробів 20 стандартних. Знайти ймовірність того, що серед навмання вийнятих 5 виробів стандартними будуть 3 вироби.

Розв’язання. .

.

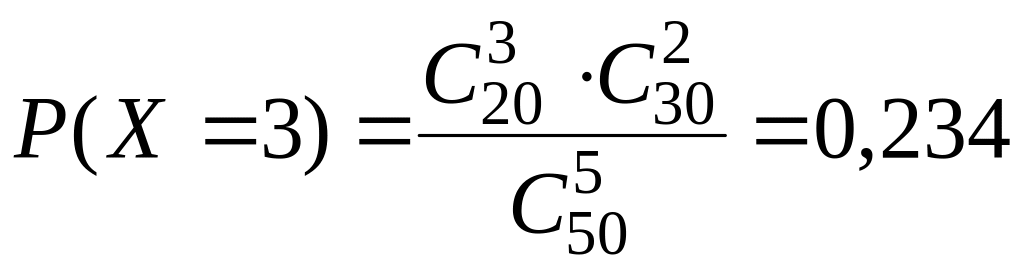Числовими характеристиками випадкових величин є математичне сподівання, дисперсія, середнє квадратичне відхилення, мода і медіана, асиметрія і ексцес.

Математичним сподіванням дискретної випадкової величини називається сума добутків значень випадкової величини на ймовірності цих значень

.

Математичне сподівання випадкової величини, розподіленої за біноміальним законом, обчислюється за формулою

,

де — число можливих значень випадкової величини;

— імовірність появи події А в такому випробуванні.

Дисперсією випадкової величини називається математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання

.

Дисперсію зручно обчислювати за формулою

.

Дисперсія випадкової величини, розподіленої за біноміальним законом, дорівнює добутку числа випробувань, на ймовірність появи й не появи події в даному випробуванні:

.

Середнім квадратичним відхиленням випадкової величини називається квадратний корінь із дисперсії:

.

Властивості математичного сподівання (МС)

1. МС постійної величини дорівнює їй самої .

2. Постійний множник можна виносити за знак МС.

3. МС суми випадкових величин дорівнює МО доданків:

.

4. МС добутку взаємно незалежних випадкових величин дорівнює добутку МС співмножників

.

5. МС біноміального розподілу дорівнює добутку числа випробувань на ймовірність появи події при даному випробуванні

.

Властивості дисперсії

1. Дисперсія сталої дорівнює нулю .

2. Постійний множник можна виносити за знак дисперсії, попередньо звівши його у квадрат:

.

3. Дисперсія суми незалежних випадкових величин дорівнює сумі дисперсій доданків:

.

4. Дисперсія біноміального розподілу дорівнює добутку числа випробувань на ймовірність появи й не появи події в одному випробуванні

.

Модою дискретної випадкової величини х називається найбільш ймовірне її можливе значення.

Медіаною випадкової величини х таке її можливе значення, для якого справджується рівність

.

Початковим моментом порядку випадкової величини х називається математичне сподівання величини и обозначається:

.

Для д.в.в.

.

Центральним моментом порядку випадкової величини х називається математичне сподівання величини и обозначається:

.

Для д.в.в.

.

Приклад 1. Знайти МС дискретної випадкової величини , заданої законом розподілу:

х	– 4	6	10
р	0,2	0,3	0,5

Розв’язання: МС = .

Приклад 2. Знайти МС випадкової величини z, якщо відомі МС х и у:

.

Розв’язання. .

Приклад 3. Знайти МС дискретної випадкової величини х – числа кидків п'яти гральних кубиків, у кожному з яких на двох кубиках з'явиться по одному очку, якщо загальне число кидків дорівнює 20.

Розв’язання. .

За формулою Бернуллі:

.

.

.

Приклад 4. Імовірність того, що в бібліотеці необхідна студентові книга вільна, дорівнює 0,3. Скласти закон розподілу випадкової величини х – числа бібліотек, які відвідає студент, якщо в місті 4 бібліотеки. Обчислити МС й дисперсію цієї випадкової величини.

Розв’язання. х = 1 (якщо книга є в бібліотеці). = 1, 2, 3, 4.

1) Якщо книга є в першій бібліотеці: .

2) Якщо книга є в 2-й бібліотеці, то .

3) Якщо книга є в 3-й бібліотеці, то .

4) Якщо книга є в 4-й бібліотеці, то .

5) таким чином, закон розподілу представимо в таблиці:

х	1	2	3	4
р	0,3	0,21	0,147	0,343

Контроль: 0,3 + 0,21 + 0,147 + 0,343 = 1.

6) МС даної випадкової величини:

.

7) Для обчислення дисперсії складемо спочатку закон розподілу випадкової величини :

	1	4	9	16
р	0,3	0,21	0,147	0,343

.

8) Тоді

.

Приклад 5. Знайти дисперсію й середнє квадратичне відхилення дискретної випадкової величини х, заданої законом розподілу:

х	-5	2	3	4
р	0,4	0,3	0,1	0,2

Розв’язання. За формулою

1) МС: .

2) Складемо закон розподілу для :

	25	4	9	16
Р	0,4	0,3	0,1	0,2

3) Знайдемо МС для :

.

4) Знайдемо шукану дисперсію:

.

5) Знайдемо середнє квадратичне відхилення:

.

Приклад 6. Знайти дисперсію дискретної випадкової величини х – числа появи події А в п'ятьох незалежних випробуваннях, якщо ймовірність появи події А в кожнім випробуванні дорівнює 0,2.

Розв’язання. (незалежно, с однаковою ймовірністю).

За умовою: п = 5, р = 0,2, q = 1 – 0,2 =0,8.

Тоді:

.

Приклад 7. Дискретна випадкова величина х задана законом розподілу:

х	4	8	12
р	0,5	0,2	0,3

Знайти функцію розподілу й накреслити її графік.

Розв’язання.

1) Якщо , то .

2) Якщо , то , тому що величина х може прийняти значення з імовірністю 0,5.

3) Якщо , то , тому що х може прийняти значення 4 з імовірністю 0,5; а 8 з імовірністю 0,2; по сумі ймовірностей .

4) Якщо , то ймовірність , тому що – достовірна.