3.1 Випадкові величини та функції розподілу

Змінна величина , яка в результаті випробування приймає дійсне значення, яке можна виразити за допомогою числа, називається випадковою величиною.

Випадкові величини можуть бути дискретними й неперервними.

Випадкова величина вважається заданою, якщо задані всі можливі її значення й відповідні їм імовірності, тобто значення випадкової величини характеризується певною ймовірністю.

Відповідність між значенням випадкової величини й ймовірностями називається законом розподілу випадкової величини.

Загальними законами розподілу для д.в.в. є ряд розподілу й функція розподілу.

Рядом розподілу д.в.в. називається таблиця, перший рядок якої містіть можливі значення випадкової величини а другий – відповідні їм імовірності .

х				…
р				…

Функція називається функцією розподілу випадкової величини , якщо для будь-якого визначена ймовірність того, що прийме значення менше ніж , тобто і

. (1)

Властивості функції розподілу

1.

2. Функція розподілу є не спадною: якщо , то

.

3. Функція розподілу неперервна зліва:

.

4. Імовірність попадання в інтервал:

.

5. .

6. .

3.2 Дискретні випадкові величини

Дискретною називають випадкову величину, можливі значення якої є окремі ізольовані числа.

Законом розподілу дискретної випадкової величини називається перелік її можливих значень і відповідних їм імовірностей.

Закон розподілу може бути заданий у вигляді таблиці:

х				…
р				…

Біноміальним називається закон розподілу дискретної випадкової величини Х – числа появи подій у незалежних випробуваннях, у кожному з яких імовірність появи подій дорівнює ; імовірність можливого значення (числа k появ події обчислюється за формулою Бернуллі):

.

Закон розподілу можна зобразити графічно – багатокутником розподілу або полігоном.

Приклад 1. На винищувачі є по дві ракети двох типів. По однієї й тій же цілі намічений дослідницький пуск спочатку ракетами першого, а потім другого типу. Пуск припиняється після першого влучення ракети. Визначити закон розподілу невитрачених ракет.

Імовірність влучення при пуску ракети першого типу , а другого типу – .

Розв’язання. – число невитрачених ракет.

Можливі значення: .

.

.

.

.

Ряд розподілу

	0	1	2	3
	0,245	0,245	0,21	0,3

Багатокутник розподілу

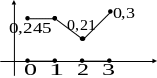
Якщо число випробувань велике, а ймовірність р появи події в кожному випробуванні дуже мала, то використовують наближену формулу Пуассона

,

де — число появи події в п незалежних випробуваннях;

— середнє число появи події в п випробуваннях — кажуть, що випадкова величина розподілена за законом Пуассона.

Приклад 2. Пристрій складається з трьох незалежно працюючих елементів. Ймовірність відмови кожного елемента в одному досвіді дорівнює 0,1. Скласти закон розподілу числа елементів, які відмовили в одному досліді.

Розв’язання. Величина Х — число елементів, які відмовили в одному досвіді, має наступні можливі значення:

( відмовили всі три елементи).

За формулою Бернуллі, отримаємо

.

.

.

.

Контроль: .

Бажаний біноміальний закон розподілу Х:

	0	1	2	3
	0,729	0,243	0,027	0,001

Приклад 3. (на розподіл Пуассона) Підручник видано кількістю 100000 примірников. Ймовірність того, що підручник сброшюруван неправильно, дорівнює 0,0001. Знайти ймовірність того, що тираж містить рівно п'ять бракованих книг.

Розв’язання. .

п — велике, а р — мале, за законом розподілу Пуассона

1) .

2) Шукана вірогідність:

.

Геометричний розподіл

Якщо проводяться п незалежних подій з ймовірністю появи події А , які закінчуються при перший появі події А , то ймовірність такої події за теоремою добутку ймовірностей незалежних подій

При цьому:

.

Приклад 4. Проводиться стрільба по мішені до першого влучення. Ймовірність влучення в ціль . Знайти ймовірність того, що влучення буде при третьому пострілі.

Розв’язання. .

.