2.2 Электрические цепи переменного тока

Электрические цепи могут находиться под воздействием переменных напряжений и токов. Среди этих воздействий важнейшую роль играют гармонические колебания. Последние широко используются для передачи сигналов и электрической энергии, а также могут применяться в качестве простейшего испытательного сигнала. Исследование режима гармонических колебаний важно и с методической точки зрения, поскольку анализ электрических цепей при негармонических воздействиях можно свести к анализу цепи от совокупности гармонических воздействий. В этом смысле методику анализа и расчета цепей при гармонических воздействиях можно распространить и на цепи при периодических несинусоидальных, а также непериодических воздействиях.

Гармоническое колебание i(t) характеризуется следующими основными параметрами: амплитудой I_m, угловой частотой , начальной фазой ₀. Начальная фаза определяется формулой j₀ = wt₀, так как j = wt (или t = j/w).

Аналитически гармонические колебания можно определить уравнением: i(t) = = I_msin(t + ₀). Для питания различных электроэнергетических установок ещё в СССР была принята промышленная частота f = 50 Гц. Важными параметрами гармонических колебаний являются их действующее и среднее значения. Действующее значение гармонического тока определяется выражением

. (2.21)

После интегрирования получим для действующего значения тока:

. (2.22)

Аналогично определяется действующее значение напряжения: U  0,707U_m. Действующие значения токов и напряжений называют еще их среднеквадратичными значениями.

Среднее значение гармонического тока определяется формулой . А средневыпрямленное напряжение имеет значение, соответствующее выражению .

Гармонические колебания можно представить различными способами: функциями времени (временные диаграммы); вращающимися векторами (векторные диаграммы); комплексными числами; амплитудными и фазовыми спектрами. Тот или иной способ представления зависит от характера решаемых задач.

Временное представление гармонических колебаний наглядно, однако его использование в задачах анализа цепей затруднительно, так как требует проведения громоздких тригонометрических преобразований.

Задание 20. Пусть в розетке вашей квартиры косинусоидальное напряжение 220 В 50 Гц. Определите его амплитудное, средневыпрямленное и среднее значения, период и начальную фазу. Приведите графическое изображение напряжения в розетке, отметив на нём найденные вами напряжения.

При выполнении задания используйте [3, 4] и приведённый выше материал. Уясните физическое понимание среднеквадратичного, средневыпрямленного и среднего напряжений. При решении задачи получите формулы, связывающие амплитуду со среднеквадратичным и средневыпрямленным значением. Также вам необходимо понимание графической интерпретации интеграла. Вспомните понятия циклической и угловой частоты, определение периода сигнала и начальной фазы.

Векторное представление гармонических колебаний

Более удобно векторное представление гармонических колебаний, при котором каждому колебанию ставится в соответствие вращающийся вектор определенной длины с заданной начальной фазой. На рисунке 16,а показано векторное представление двух колебаний i₁ и i₂: i₁ = I_m1sin(t + ₁); i₂ = I_m2sin(t + ₂).

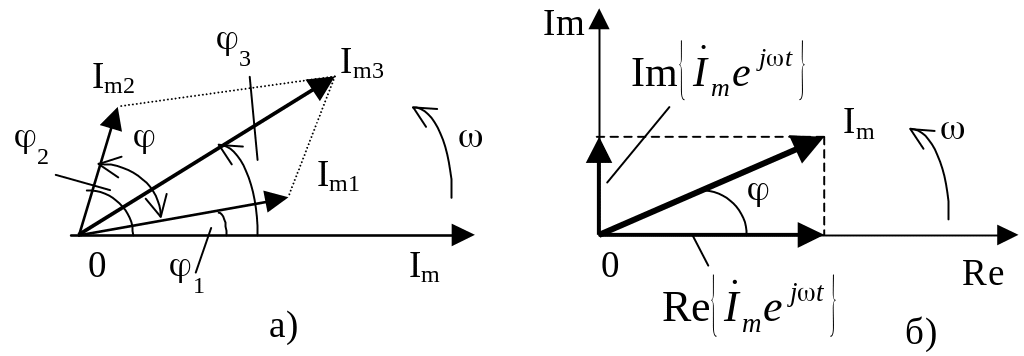
Рисунок 16 – Представление гармонических колебаний

Их сумму i₃ можно найти по формулам суммирования векторов:

i₃ = i₁ + i₂ = I_m3sin(t + ₃), (2.23)

где ; (2.24)

. (2.25)

Величина  = ₂ – ₁ называется фазовым сдвигом между колебаниями i₁ и i₂. Совокупность векторов, изображающих гармонические колебания в электрической цепи, называют векторной диаграммой. Векторные диаграммы можно строить как для амплитудных, так и для действующих значений токов и напряжений.

Задание 21. В электрической цепи, состоящей из последовательно соединённых резистора сопротивлением 20 Ом и катушки индуктивности с индуктивностью 50 мГн под воздействием гармонического частотой 50 Гц протекает ток 2 А с начальной фазой π/6. Определите падение напряжения отдельно на элементах цепи и на полном участке цепи. Также постройте векторные диаграммы всех указанных напряжений, если падение напряжения на индуктивности опережает падение напряжения на резисторе на 90^Ο.

При выполнении задания используйте литературу [3, 4] и приведённые выше формулы и графики. Определите падение напряжения на участках цепи по закону Ома. Строя векторную диаграмму в полярной системе координат, отложите векторы падений напряжений на сопротивлении и индуктивности, выбрав масштаб, а затем произведите графическое суммирование векторов.

Сравните полученный результат с суммарным вектором, полученным аналитически.

Представление гармонических колебаний с помощью комплексных чисел

Наиболее распространенными являются представления гармонических колебаний с помощью комплексных чисел. Представим ток i на комплексной плоскости. Для этого изобразим вектор I_m на комплексной плоскости с учетом начальной фазы  (рисунок 16,б). Будем вращать этот вектор в положительном направлении (против часовой стрелки) с угловой частотой . Тогда в любой момент времени положение вращающегося вектора определится комплексной величиной (комплексным гармоническим колебанием):

i(t) = I_me^{j( t +  )} = I_mcos(t + _i) + jI_msin(t + _i). (2.26)

Первая часть слагаемого отражает проекцию вращающегося вектора на вещественную ось, а вторая часть – на мнимую ось.

Оценив второе слагаемое, приходим к выводу: синусоидальный ток i на комплексной плоскости представляется в форме проекции на мнимую ось вращающегося вектора:

i = Im[I_me^{j( t +  )}] = Im[ _me^jwt] , (2.27)

где Im – сокращенное обозначение слова Imaginarins (мнимый): . Величина носит название комплексной амплитуды тока.

Если гармоническое колебание задается в форме косинусоиды, то на комплексной плоскости этому току соответствует проекция вектора на вещественную ось:

i = Re[I_me^{j( t +  )}] = Re[ _me^jwt], (2.28)

где Re – сокращенное обозначение слова Realis (действительный, вещественный). Комплексную амплитуду синусоидальной функции заданной частоты можно рассматривать как преобразование временной функции в частотную область.

Задание 22. На резисторе сопротивлением 30 Ом имеется падение напряжения переменного тока (частота 50 Гц) амплитудой 311 В и начальной фазой /3). Определите синусоидальные и косинусоидальные составляющие этого падения напряжения.

При выполнении задания используйте работы [3, 4] и приведённые выше формулы и график на рисунке 16,б. Определите составляющие напряжения математически и графически. Делая построения на комплексной плоскости, выберите масштаб, и произведите необходимые оценки обеих составляющих.

Сравните результаты, полученные математически и графически.

Фазовый сдвиг мъежду напряжением и током в элементах цепи

Гармонические колебания в пассивных RLC-цепях ведут себя по-разному. Если к резистивному элементу R приложено синусоидальное гармоническое напряжение, то ток i и напряжение u в резистивном элементе совпадают по фазе друг с другом (рисунок 17,а).

В индуктивности под действием напряжения будет протекать ток (c учётом, что :

, (2.29)

где I_m = U_m/( L) = U_m/X_L; X_L – индуктивное сопротивление; _i = _u – /2 – начальная фаза тока. Ток в индуктивности отстает от приложенного напряжения на /2, рисунок 17,б):  = _u – _i = /2.

Рисунок 17 – Векторные диаграммы для RLC–цепей

Для емкостного элемента, с учётом, что

имеем:

i = C =C U_msin(t + _u + p/2) = I_msin(t + _i) , (2.30)

где I_m = U_m/(1/С); _i = _u + /2 – начальная фаза тока. Величину X_C = 1/(C) называют емкостным сопротивлением. Видно, что ток в емкости опережает приложенное напряжение на /2 (рисунок 17,в).

Задание 23. В электрической цепи, состоящей из последовательно соединённых резистора сопротивлением 20 Ом, катушки индуктивности с индуктивностью 50 мГн и ёмкости 50 мкФ под воздействием приложенного напряжения частотой 50 Гц протекает ток 1 А с начальной фазой /4. Определите падение напряжения отдельно на каждом из элементов и приложенное к цепи. Также постройте векторные диаграммы всех указанных напряжений.

При выполнении задания используйте литературу [3, 4], приведённые выше формулы и графики рисунка 17. Определите падение напряжения на участках цепи по закону Ома. Строя векторную диаграмму в полярной системе координат, отложите векторы падений напряжений на сопротивлении, индуктивности и ёмкости, выбрав масштаб, а затем произведите графическое суммирование векторов для получения приложенного к цепи напряжения.