146 Глава 3. Цифровой логический уровень

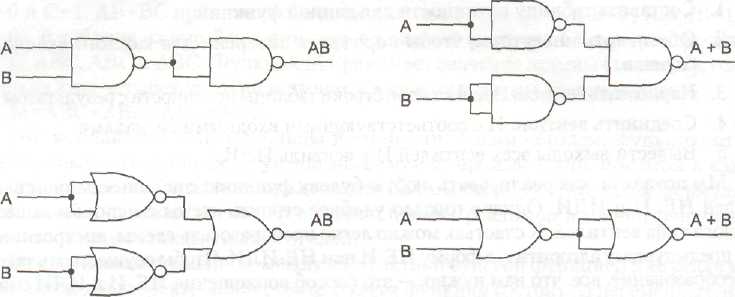
Рис. 3.4. Конструирование вентилей НЕ (а), И (б) и ИЛИ (в) с использованием только вентилей НЕ-И или только вентилей НЕ-ИЛИ

В качестве примера использования булевой алгебры рассмотрим схему и таб­лицу истинности для АВ+АС (рис. 3.5, а). Хотя мы это еще не обсуждали, многие правила обычной алгебры имеют силу для булевой алгебры. Например, выраже­ние АВ+АС может быть преобразовано в А(В+С) с помощью дистрибутивного за­кона. На рис. 3.5, б" показана схема и таблица истинности для А(В+С). Две функ­ции являются эквивалентными тогда и только тогда, когда обе функции принимают одно и то же значение для всех возможных переменных. Из таблиц истинности на рис. 3.5 ясно видно, что А(В+С) эквивалентно АВ+АС. Несмотря на эту эквива­лентность, схема на рис. 3.5, б" лучше, чем схема на рис. 3.5, а, поскольку она содер­жит меньше вентилей.

Обычно разработчик исходит из определенной булевой функции, а затем приме­няет к ней законы булевой алгебры, чтобы найти более простую функцию, эквива­лентную исходной. На основе полученной функции можно конструировать схему.

Чтобы использовать данный подход, нам нужны некоторые равенства из буле­вой алгебры. В табл. 3.1 показаны некоторые основные законы. Интересно отме­тить, что каждый закон имеет две формы. Одну форму из другой можно получить, меняя И на ИЛИ и 0 на 1. Все законы можно легко доказать, составив их таблицы истинности. Почти во всех случаях результаты очевидны, за исключением законов Де Моргана, законов поглощения и дистрибутивного закона А+ВС=(А+В)(А+С). Законы Де Моргана распространяются на выражения с более чем двумя перемен­ными, например АВС=А+В+С.

Вентили и булева алгебра

147

А(В + С)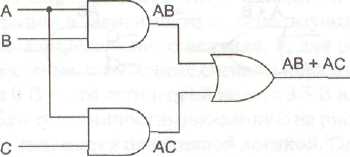

А	в	с	АВ	АС	АВ + АС		А	в	с	А	в + с	А(В + С}
0	0	0	0	0	0		0	0	0	0	0	0
0	0	1	0	0	0		0	0	1	0	1	0
0	1	0	0	0	0		0	1	0	0	1	0
0	1	1	0	0	0		0	1	1	0	1	0
1	0	0	0	0	0		1	0	0	1	0	0
1	0	1	0	1	1		1	0	1	1	1	1
1	1	0	1	0	1		1	1	0	1	1	1
1	1	1	1	1	1		1	1	1	1	1	1

Рис. 3.5. Две эквивалентные функции: АВ+АС (а); А(В+С) (б).

Таблица 3.1. Некоторые законы булевой алгебры Названия законов И ИЛИ

1А=А	0+А-А
0А=0 АА=А	1+А=1 А+А=А
АА=О	А+А=1
АВ=ВА	А+В=В+А
(АВ)С=А(ВС)	(А+В)+С=А+(В+С)
А+ВС=(А+В)(А+С)	А(В+С)=АВ+АС
А(А+В)=А	А+АВ=А
АВ=А+В	А+В=А В

Законы тождества Законы нуля

Законы идемпотентности Законы инверсии Коммуникативные законы Ассоциативные законы Дистрибутивные законы Законы поглощения Законы Де Моргана

Законы Де Моргана предполагают альтернативную запись. На рис. 3.6, а форма И дается с отрицанием, которое показывается с помощью инвертирующих входов и выходов. Таким образом, вентиль ИЛИ с инвертированными входными сигна­лами эквивалентен вентилю НЕ-И. Из рис. 3.6, б, на котором изображена вторая форма закона Де Моргана, ясно, что вместо вентиля НЕ-ИЛИ можно нарисовать вентиль И с инвертированными входами. С помощью отрицания обеих форм зако­на Де Моргана мы приходим к эквивалентным репрезентациям вентилей И и ИЛИ (см. рис. 3.6, в и 3.6, г). Аналогичные символические изображения существуют для различных форм закона Де Моргана (например, n-входовый вентиль НЕ-И стано­вится вентилем ИЛИ с инвертированными входами).

148