Основные цифровые логические схемы

157

мой логической матрицы более эффективно, чем применение двух других мето­дов. Для простых схем предпочтительнее более дешевые МИС и СИС.

Арифметические схемы

Перейдем от СИС общего назначения к комбинационным схемам СИС, которые используются для выполнения арифметических операций. Мы начнем с простой 8-разрядной схемы сдвига, затем рассмотрим структуру сумматоров и, наконец, изучим арифметико-логические устройства, которые играют существенную роль в любом компьютере.

Схемы сдвига

Первой арифметической схемой СИС, которую мы рассмотрим, будет схема сдви­га, содержащая 8 входов и 8 выходов (рис. 3.15). Восемь входных битов подаются на линии Do,..., D₇. Выходные данные, которые представляют собой входные дан­ные, сдвинутые на 1 бит, поступают на линии So,..., S₇. Линия управления С опре­деляет направление сдвига: 0 — налево, 1 — направо.

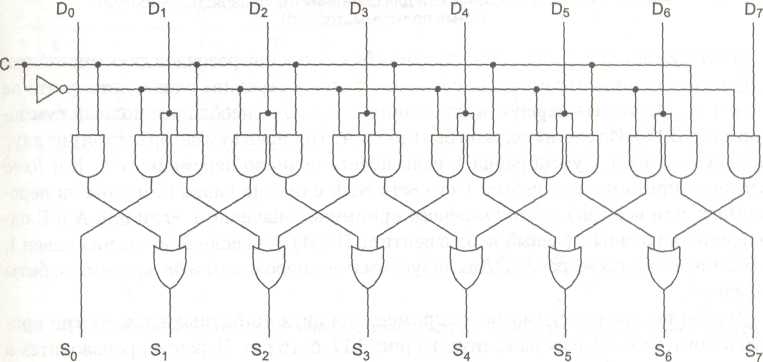
Рис. 3.15. Схема сдвига

Чтобы понять, как работает такая схема, рассмотрим пары вентилей И (кроме крайних вентилей). Если С=1, правый член каждой пары включается, пропуская через себя соответствующий бит. Так как правый вентиль И соединен с входом вентиля ИЛИ, который расположен справа от этого вентиля И, происходит сдвиг вправо. Если С=0, включается левый вентиль И из пары, и тогда происходит сдвиг влево.

Сумматоры

Компьютер, который не умеет складывать целые числа, практически немыслим. Следовательно, схема для выполнения операций сложения является существен­ной частью любого процессора. Таблица истинности для сложения одноразряд-

158

Глава 3. Цифровой логический уровень

ных целых чисел показана на рис. 3.16, а. Здесь имеется два результата: сумма вход­ных переменных А и В и перенос на следующую (левую) позицию. Схема для вы­числения бита суммы и бита переноса показана на рис. 3.16, б. Такая схема обычно называется полусумматором.

Вентиль ИСКЛЮЧАЮЩЕЕ ИЛИ

А	В	Сумма	Перенос
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

А В-

Сумма

Перенос

Рис. 3.16. Таблица истинности для сложения одноразрядных чисел (а); схема полусумматора (б)

Полусумматор подходит для сложения битов нижних разрядов двух многобито­вых слов. Но он не годится для сложения битов в середине слова, потому что не может осуществлять перенос в эту позицию. Поэтому необходим полный сумма­тор (рис. 3.17). Из схемы должно быть ясно, что полный сумматор состоит из двух полусумматоров. Сумма равна 1, если нечетное число переменных А, В и Вход переноса принимает значение 1 (то есть если единице равна или одна из пере­менных, или все три). Выход переноса принимает значение 1, если или А и В од­новременно равны 1 (левый вход в вентиль ИЛИ), или если один из них равен 1, а Вход переноса также равен 1. Два полусумматора порождают и биты суммы, и биты переноса.

Чтобы построить сумматор, например, для двух 16-битных слов, нужно про­дублировать схему, изображенную на рис. 3.17, б, 16 раз. Перенос производится в левый соседний бит. Перенос в самый правый бит соединен с 0. Такой сумматор называется сумматором со сквозным переносом. Прибавление 1 к числу 111... 111 не осуществится до тех пор, пока перенос не пройдет весь путь от самого правого бита к самому левому. Существуют более быстрые сумматоры, работающие без подобной задержки. Естественно, предпочтение обычно отдается им.

Рассмотрим пример более быстрого сумматора. Разобьем 32-разрядный сум­матор на 2 половины: нижнюю 16-разрядную и верхнюю 16-разрядную. Когда на­чинается сложение, верхний сумматор еще не может приступить к работе, посколь­ку он не узнает значение переноса, пока не совершится 16 суммирований в нижнем сумматоре.

Однако можно сделать одно преобразование. Вместо одного верхнего суммато­ра можно получить два верхних сумматора, продублировав соответствующую часть аппаратного обеспечения. Тогда схема будет состоять из трех 16-разрядных сум-

Основные цифровые логические схемы

159

маторов: одного нижнего и двух верхних U0 и U1, которые работают параллельно. В сумматор U0 в качестве переноса поступает 0, а в сумматор U1 в качестве перено­са поступает 1. Оба верхних сумматора начинают работу одновременно с нижним сумматором, но только один из результатов суммирования в двух верхних сумма­торах будет правильным. После сложения 16 нижних разрядов становится извест­но значение переноса в верхний сумматор, и тогда можно определить правильный ответ. При таком подходе время сложения сокращается в два раза. Такой сумма­тор называется сумматором с выбором переноса. Можно разбить каждый 16-раз­рядный сумматор на два 8-разрядных и т. д.

Выход переноса

В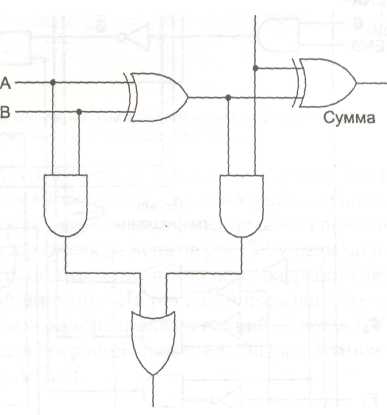 ход переноса

А	в	Вход переноса	Сумма	Выход переноса
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

Рис. 3.17. Таблица истинности для полного сумматора (а); схема для полного сумматора (б)

Арифметико-логические устройства

Большинство компьютеров содержат одну схему для выполнения операций И, ИЛИ и сложения над двумя машинными словами. Обычно такая схема для п-бит-ных слов состоит из п идентичных схем для индивидуальных битовых позиций. На рис. 3.18 изображена такая схема, которая называется арифметико-логичес­ким устройством, или АЛУ. Это устройство может вычислять одну из 4 следую­щих функций: А И В, А ИЛИ В, В и А+В. Выбор функции зависит от того, какие сигналы поступают на линии F_o и F_t: 00, 01, 10 или 11 (в двоичной системе счисле­ния). Отметим, что здесь А+В означает арифметическую сумму А и В, а не логичес­кую операцию И.

В левом нижнем углу схемы находится двухразрядный декодер, который по­рождает сигналы включения для четырех операций. Выбор операции определяет-

160