- •I. Механика жидкости и газов техническая гидромеханика
- •Краткая теория
- •Описание лабораторной установки
- •Руководство по эксплуатации терморегулятора
- •Порядок проведения опыта
- •Обработка результатов опыта
- •Общие сведения
- •Описание опытной установки
- •Порядок проведения работы
- •Общие сведения
- •Описание опытной установки
- •Порядок выполнения лабораторной работы
- •Обработка опытных данных
- •«Определение коэффициента гидравлического трения при движении жидкости в круглой трубе»
- •Общие сведения
- •Описание опытной установки
- •Порядок выполнения работы
- •Обработка опытных данных
- •Описание опытной установки
- •Порядок проведения работы
- •Обработка опытных данных
- •Вводная часть
- •Описание опытной установки
- •Порядок выполнения лабораторной работы
- •Обработка опытных данных
- •Вводная часть
- •Описание опытной установки
- •Порядок проведения лабораторной работы
- •Обработка опытных данных
- •Общие сведения
- •Описание опытной установки
- •Порядок выполнения работы
- •Краткая теория
- •Краткая теория
- •Описание опытной установки
- •Порядок выполнения лабораторной работы
- •Обработка опытных данных
- •II. Насосы и вентиляторы
Обработка опытных данных
1. Определить объем воды V, см3, заполнения мерного бака. Размеры мерного бака: а=19 см, b=44 см.
![]() .
.
2. Определить расход Q, зная время t, с, заполнения объема воды V в мерном баке по формуле:
![]() .
.
3. Определить скорости движения воды в трубе 2 зная, что:
![]() ,
,
где ![]() – площадь поперечного сечения трубы.
– площадь поперечного сечения трубы.
4. Определить значение числа Рейнольдса
![]() ,
,
где
ν – кинематический
коэффициент вязкости воды,
![]() .
.
5. Данные занести в табл. 1 и построить график зависимости h = ƒ(υ) в прямоугольных координатах.
6. По графику
определить скорость υк в
момент перехода линейной зависимости
h=ƒ(υ) в криволинейную
и сравнить ее с величиной
![]() полученной путем измерения как:
полученной путем измерения как:
![]() .
.
7. Вычислить Reк для υк определенной по графику.
8. Привести пример расчета.
ЛАБОРАТОРНАЯ РАБОТА № 4
«Определение коэффициента гидравлического трения при движении жидкости в круглой трубе»
Цель работы:
Определить
коэффициент гидравлического трения
![]() при ламинарном и турбулентном режимах
движения жидкости по трубопроводу.
при ламинарном и турбулентном режимах
движения жидкости по трубопроводу.
Общие сведения
При движении
жидкости по прямому трубопроводу
постоянного сечения часть удельной
механической энергии затрачивается на
преодоление сил трения как внутри
жидкости, так и о стенки трубопровода
и носит название потерь напора по длине
![]() .
.
Записывая уравнение Бернулли для двух сечений потока, можно определить потери удельной энергии на участке между сечениями I-I и II-II:
 (1)
(1)
 ,
(2)
,
(2)
так как
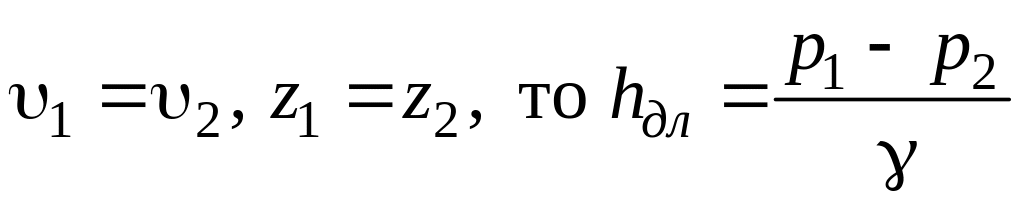 .
(3)
.
(3)
Отсюда следует, что потери напора можно определить по показаниям пьезометров, установленных в рассматриваемых сечениях.
Теоретически потери напора по длине определяются по формуле Дарси – Вейсбаха:
 (4)
(4)
где L – длина рассматриваемого участка трубопровода;
d – диаметр рассматриваемого участка;
![]() – средняя скорость
движения жидкости;
– средняя скорость
движения жидкости;
– коэффициент гидравлического трения (гидравлического сопротивления);
g – ускорение свободного падения, м/с2.
Коэффициент гидравлического трения является функцией, зависящей как от свойств жидкости (вязкости, плотности), так и параметров трубопровода (диаметра, шероховатости стенок) и условий течения (средней скорости).
Из этих независимых размерных величин можно получить два безразмерных параметра, а именно:
1. Параметр
Рейнольдса:
![]() (5)
(5)
2. Относительную
шероховатость:
![]() ,
,
то есть установить
зависимость:
![]() .
.
При ламинарном
режиме движения жидкости
![]() ,
то есть
,
то есть
![]() ,
коэффициент гидравлического трения
зависит только от числа
,
коэффициент гидравлического трения
зависит только от числа
![]() ,
,
![]() .
Для определения коэффициента
гидравлического трения используют
формулу Стокса:
.
Для определения коэффициента
гидравлического трения используют
формулу Стокса:
![]() (6)
(6)
Для турбулентного режима движения из-за сложности происходящих при этом явлений расчетные формулы для определения коэффициента гидравлического трения могут быть получены лишь при принятии определенных гипотез с последующей проверкой полученных результатов экспериментом.
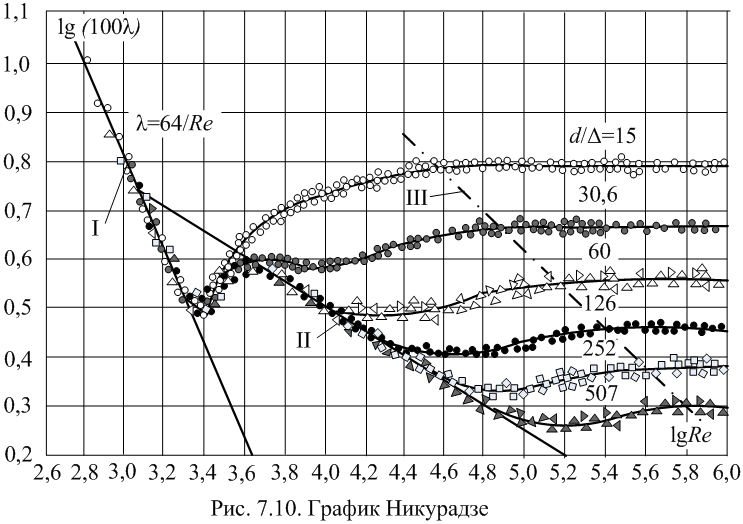
По наиболее распространенной гипотезе Прандтля турбулентный поток состоит из ядра течения и ламинарного слоя, между которыми находится переходная область (рис.1).
П ри
турбулентном режиме
ри
турбулентном режиме
![]() различают четыре основные зоны чисел
:
различают четыре основные зоны чисел
:
Если
![]() ,
то режим течения называется «переходный
турбулентный» и коэффициент гидравлического
трения определяется по формуле Френкеля:
,
то режим течения называется «переходный
турбулентный» и коэффициент гидравлического
трения определяется по формуле Френкеля:
![]() ,
(7)
,
(7)
2. При относительно
небольших числах
–
![]() – (
– (![]() – относительная шероховатость внутренней
поверхности трубопровода), когда
ламинарный слой закрывает шероховатость
стенок трубопровода, возмущения,
возникающие при обтекании жидкостью
выступов шероховатости, быстро в нем
затухают и практически не сказываются
на коэффициенте гидравлического трения.
Эта зона турбулентного режима называется
«зоной гидравлически гладких труб». В
этом случае коэффициент гидравлического
трения определяется по формуле Блазиуса:
– относительная шероховатость внутренней
поверхности трубопровода), когда
ламинарный слой закрывает шероховатость
стенок трубопровода, возмущения,
возникающие при обтекании жидкостью
выступов шероховатости, быстро в нем
затухают и практически не сказываются
на коэффициенте гидравлического трения.
Эта зона турбулентного режима называется
«зоной гидравлически гладких труб». В
этом случае коэффициент гидравлического
трения определяется по формуле Блазиуса:
![]() .
(8)
.
(8)
3. С увеличением
числа
ламинарный слой уменьшается. Когда его
толщина становится одного порядка с
высотой выступов шероховатости, то в
этой зоне коэффициент гидравлического
трения
зависит не только от числа
,
но и от шероховатости стенок:
![]() .
Эта зона смешанного трения,
.
Эта зона смешанного трения,
![]() .
Коэффициент гидравлического трения
определяют по формуле Альтшуля:
.
Коэффициент гидравлического трения
определяют по формуле Альтшуля:
![]() .
(9)
.
(9)
4. Зона, в которой
число
![]() называется зоной квадратичного
сопротивления (зона вполне шероховатых
труб). В этой зоне коэффициент
гидравлического трения
зависит только от относительной
шероховатости стенок:
называется зоной квадратичного
сопротивления (зона вполне шероховатых
труб). В этой зоне коэффициент
гидравлического трения
зависит только от относительной
шероховатости стенок:
![]() и определяется по формуле Шифринсона:
и определяется по формуле Шифринсона:
![]() .
(10)
.
(10)
Графически эти зависимости отражены в графиках Никурадзе (рис. 2).
Рис. 2. График Никурадзе |
Для новых стальных труб значение коэффициента λ может находится также по номограмме Г.А. Мурина (рис. 3).
Рис. 3. Номограмма Мурина |