
- •Содержание
- •Лабораторная работа №3
- •3.1 Постановка задачи численного интегрирования.
- •3.2 Основные методы построения квадратурных формул.
- •3.3 Оценка погрешности квадратурных формул
- •3.4 Составные квадратурные формулы
- •3.5 Метод Ричардсона практической оценки точности квадратурных формул
- •Литература
3.5 Метод Ричардсона практической оценки точности квадратурных формул
Рассмотрим приближённый метод оценки точности квадратурных формул. Приближённость метода состоит в том, что он корректен только для некоторого класса функций и полученные формулы для погрешности работают с точностью, до главных членов2. Мы же будем применять его для любых функций.
Пусть
![]() ,
при этом предположении мы получим
уточнение формулы прямоугольников.
Производя разложение в ряд Тейлора с
точностью до членов четвертого порядка
по
,
при этом предположении мы получим
уточнение формулы прямоугольников.
Производя разложение в ряд Тейлора с
точностью до членов четвертого порядка
по
![]() получим
получим
![]() ,
,
где
![]() постоянная величина независящая от
,
а
постоянная величина независящая от
,
а
![]() элементарная
квадратура прямоугольников. Величина
элементарная
квадратура прямоугольников. Величина
![]() называется главной частью погрешности
формулы прямоугольников. При этих же
предположениях, для формулы трапеций
справедливо соотношение
называется главной частью погрешности
формулы прямоугольников. При этих же
предположениях, для формулы трапеций
справедливо соотношение
![]() ,
где
,
где
![]() элементарная квадратура трапеций. Для
формулы Симпсона, при условии
элементарная квадратура трапеций. Для
формулы Симпсона, при условии
![]() имеет место равенство
имеет место равенство
![]() .Т.е.
для любой квадратурной формулы можно
выписать соотношение
.Т.е.
для любой квадратурной формулы можно
выписать соотношение
![]() .
(1)
.
(1)
Тогда, выписывая
это соотношение на шаге
![]() ,
имеем
,
имеем
![]() .
(2)
.
(2)
Вычитая из (1) равенство (2), получим
![]() .
.
Отсюда
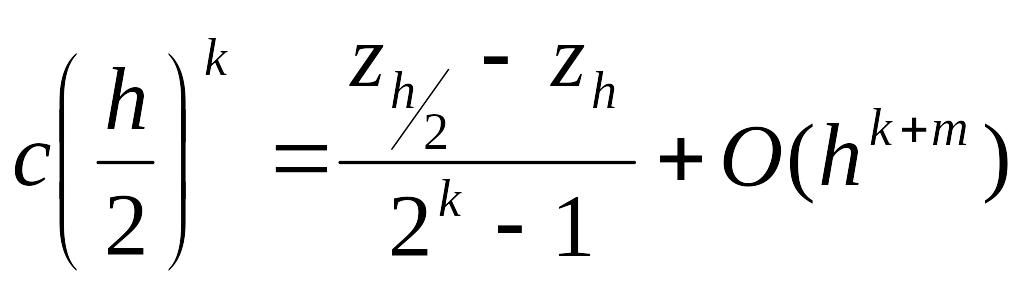
и, следовательно,
согласно (2) имеем с точностью до
![]()
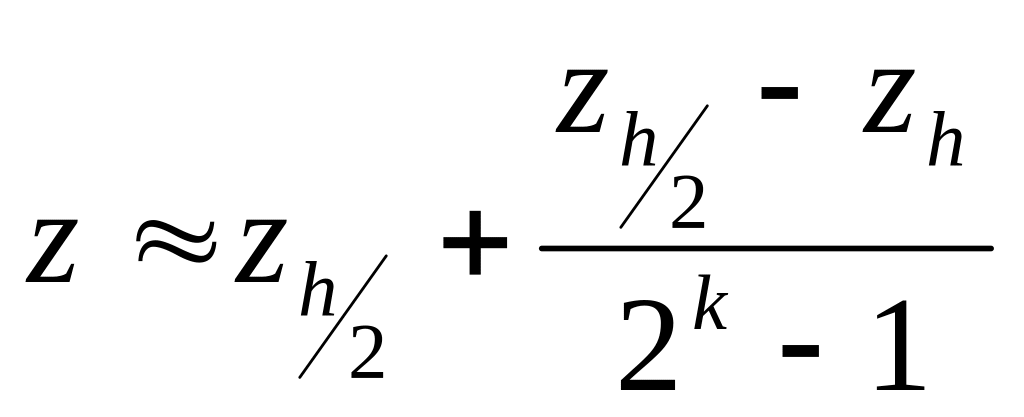 ,
(3)
,
(3)
![]() и
и
![]() известные величины,
причем величина погрешности
равна
известные величины,
причем величина погрешности
равна
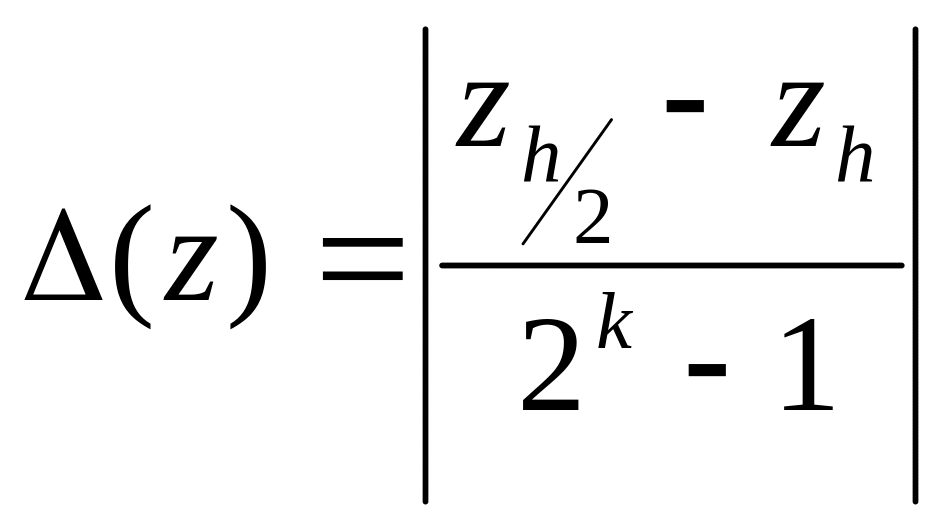 .
.
Замечание На
практике подтверждением условия
![]() является выполнение неравенства
является выполнение неравенства
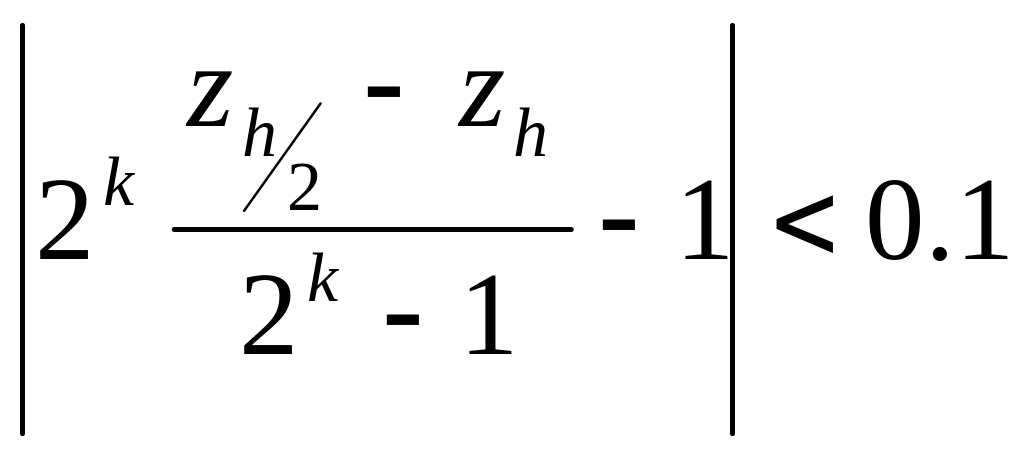 .
(4)
.
(4)
Неравенство (4)
может нарушаться последующим причинам:
а)
велико, при этом влияет отброшенный
член
;
б)
слишком мало, тогда могут сказаться
погрешности арифметики реальной ЭВМ;
в)
![]() или близко к нулю.
или близко к нулю.
Задачи для самостоятельного решения.
Используя равенство
![]()
найти с помощью
численного интегрирования приближения
к числу
![]() .
Использовать формулу прямоугольников
и формулу трапеций с элементарными
отрезками одинаковой длины
.
Использовать формулу прямоугольников
и формулу трапеций с элементарными
отрезками одинаковой длины
![]() ,
взяв
,
взяв
![]() .
Для данных
.
Для данных
![]() результат записать со всеми верными
цифрами.
результат записать со всеми верными
цифрами.
Для интеграла
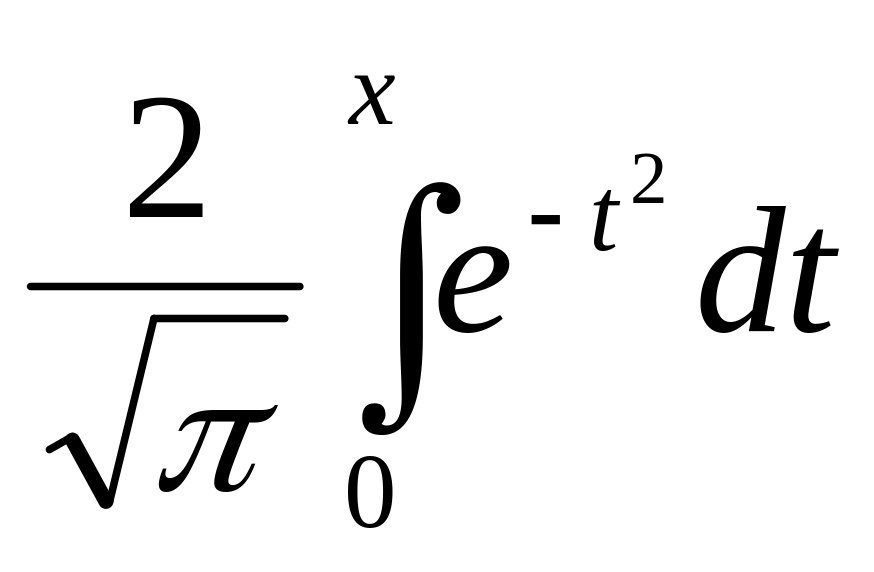 построить таблицу
построить таблицу
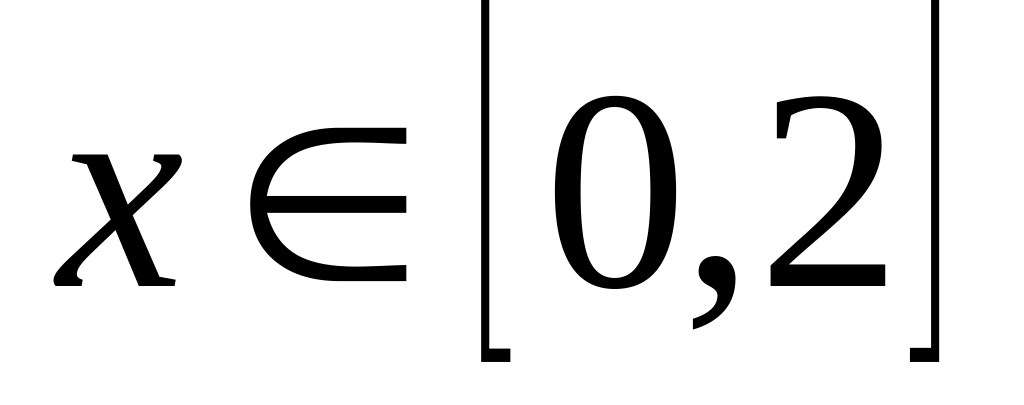 значений, с точностью
значений, с точностью
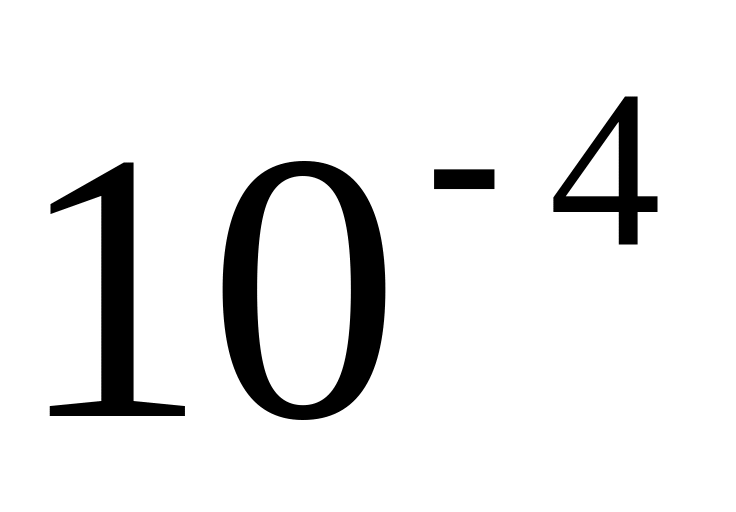 ,
допускающую линейную интерполяцию.
,
допускающую линейную интерполяцию.Используя определение интеграла Римана и теорему о среднем значении интеграла, доказать, что приближения, получаемые из квадратур прямоугольников и трапеций, сходятся при
 к интегралу. Выделите отчетливо те
предположения, которые делаются
относительно подынтегральной функции.
к интегралу. Выделите отчетливо те
предположения, которые делаются
относительно подынтегральной функции.Какой результат будет получен квадратурой Симпсона, с точностью
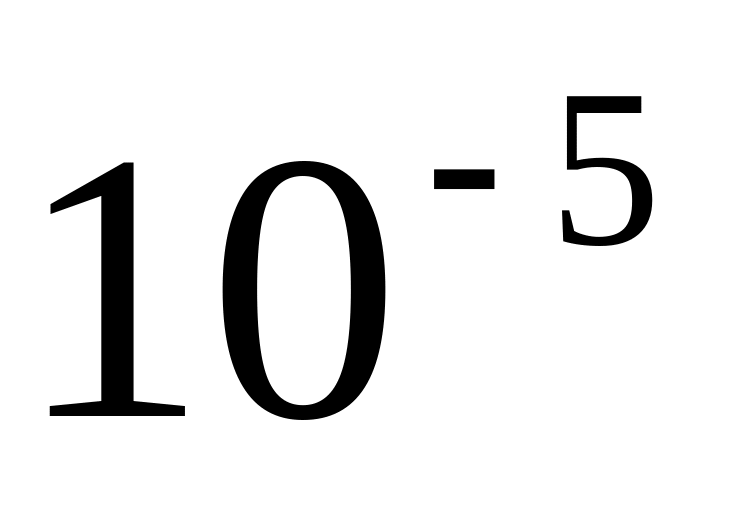 ,
для интеграла
,
для интеграла
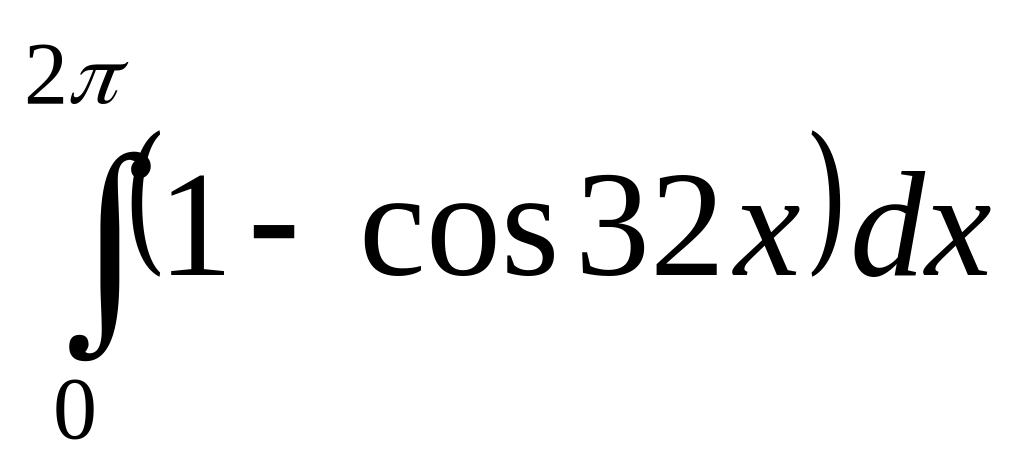 ?
Каков точный результат?
?
Каков точный результат?Опишите эффективный и “точный” метод вычисления интеграла
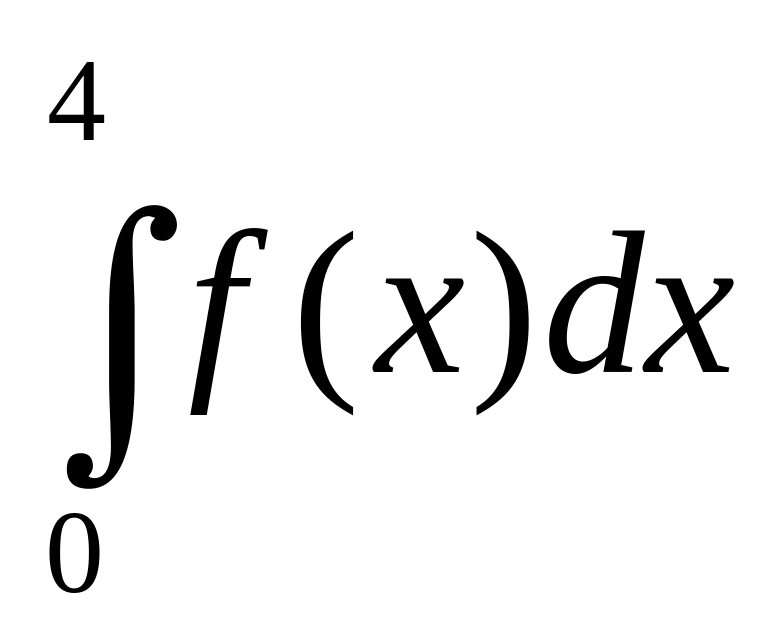 ,
где
,
где
![]() .
.
Задания к лабораторной работе.
-
№
f(x)
a
b

1
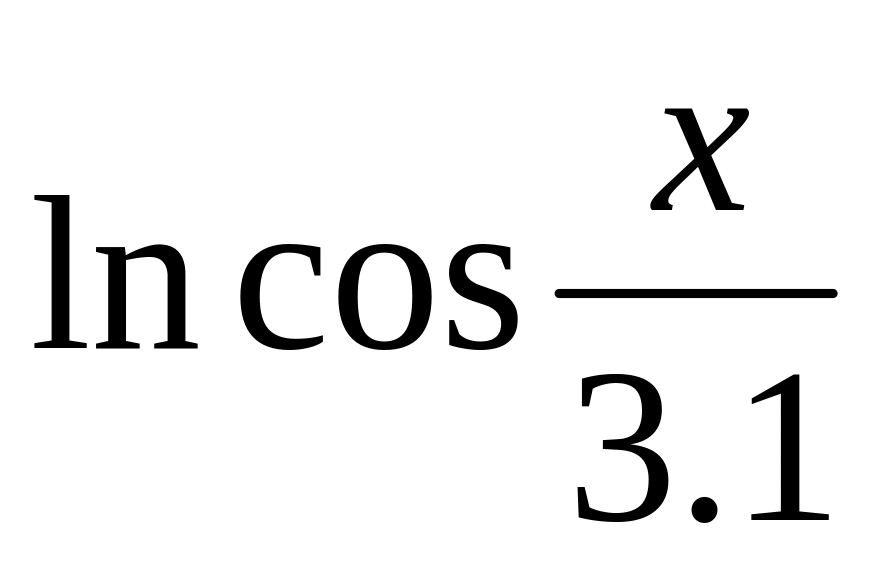
1.7
3.3
10-8
2
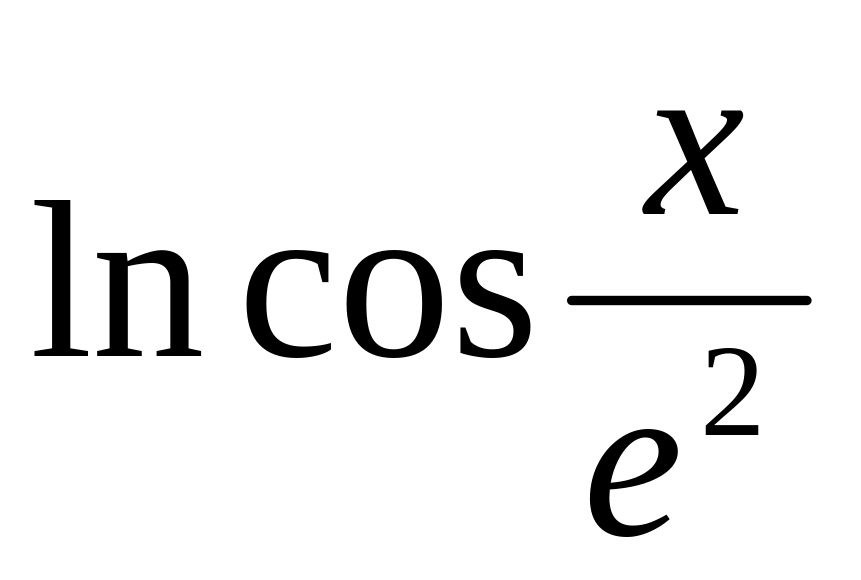
40.0
43.6
10-8
3
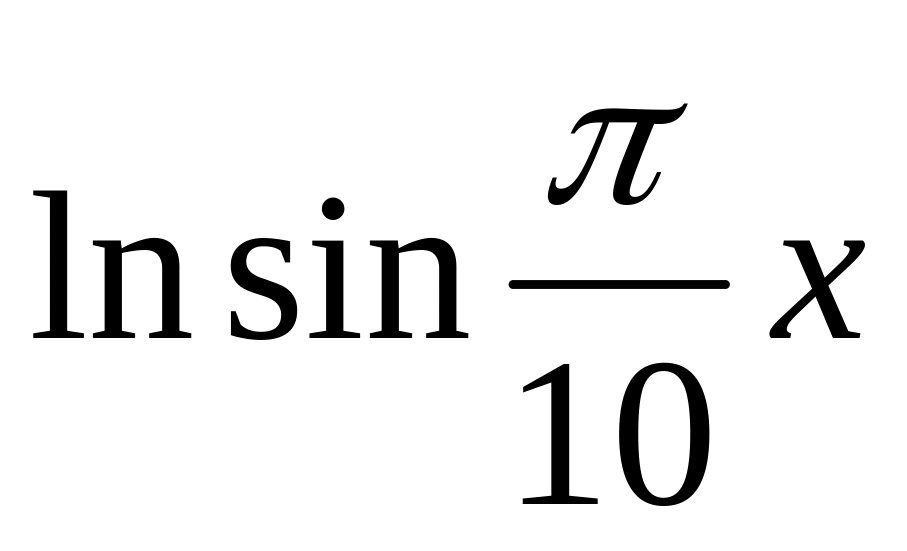
2.6
5.0
10-8
4
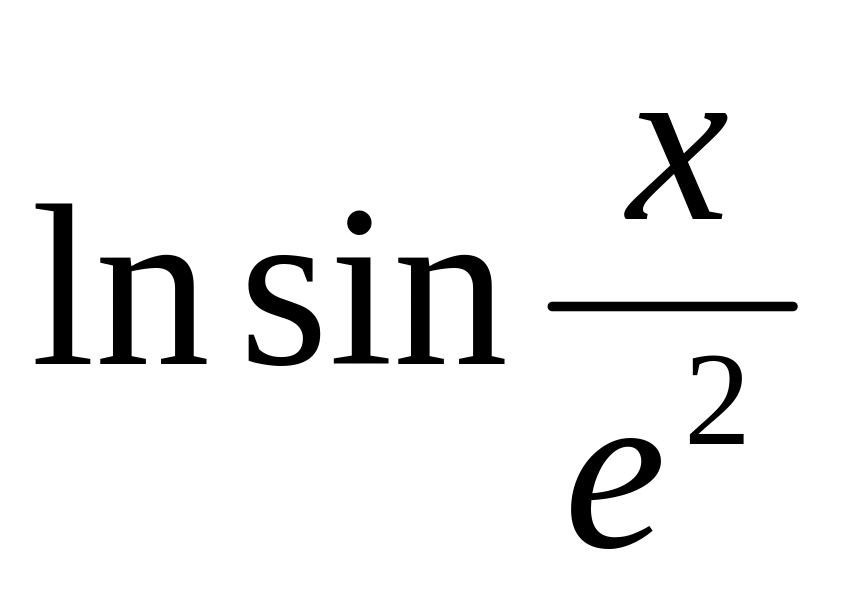
2.6
16.8
10-8
5
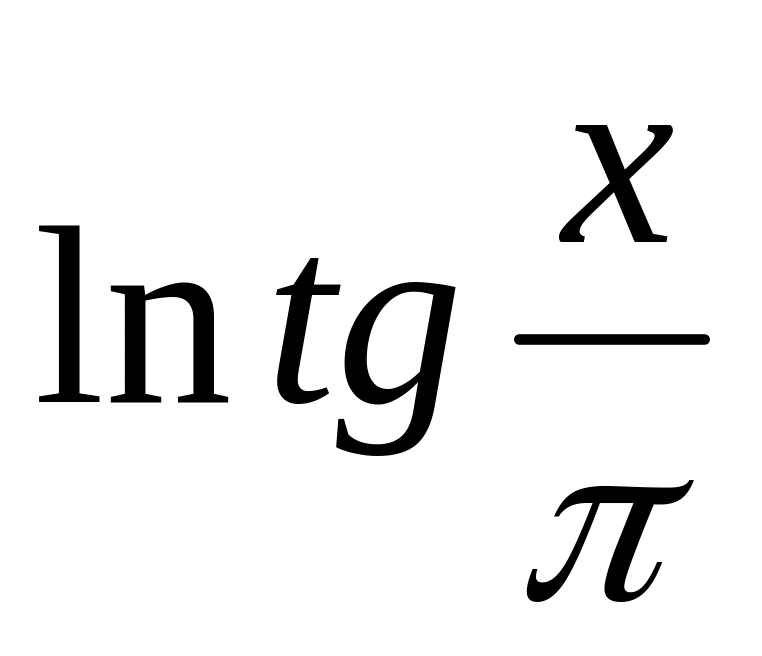
1.5
3.1
10-8
6
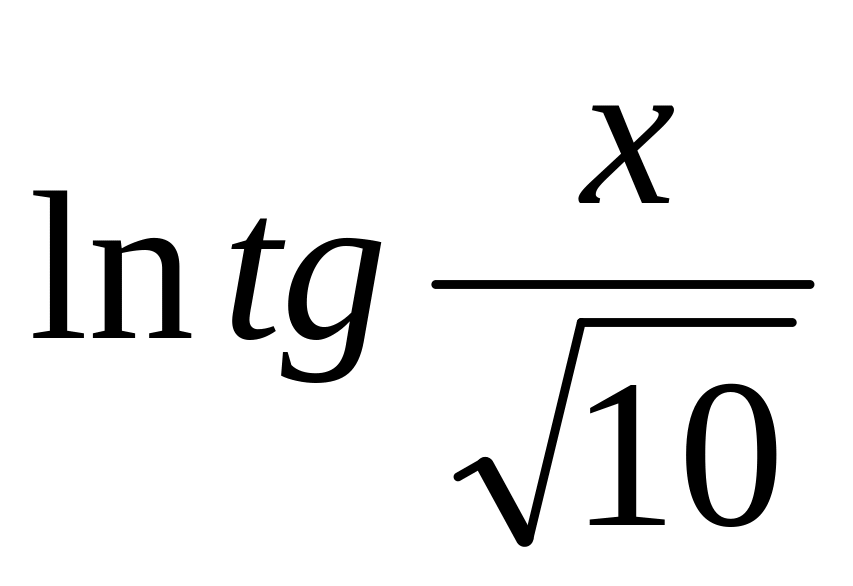
1.8
3.4
10-8
7
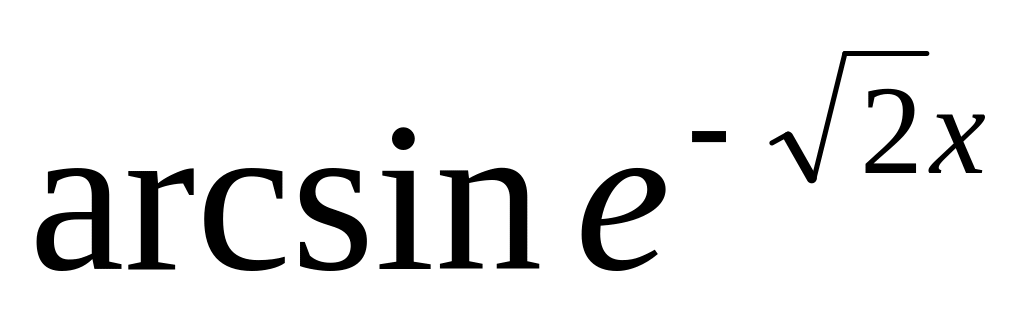
0.7
1.5
10-8
8

7
15
10-8
9
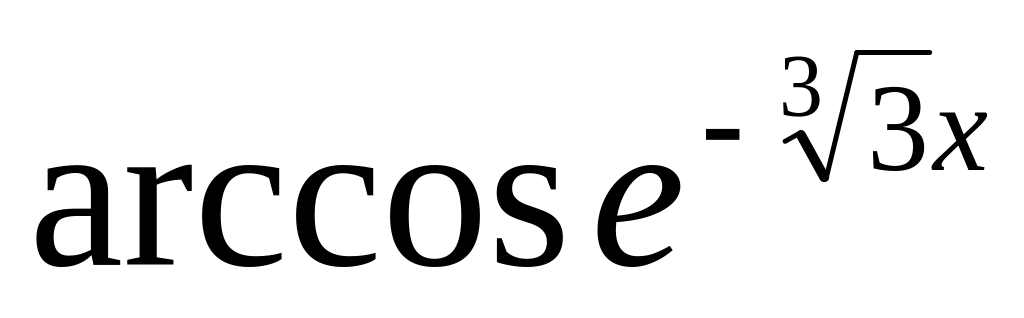
0.20
0.56
10-8
10

2.2
7.0
10-8
11
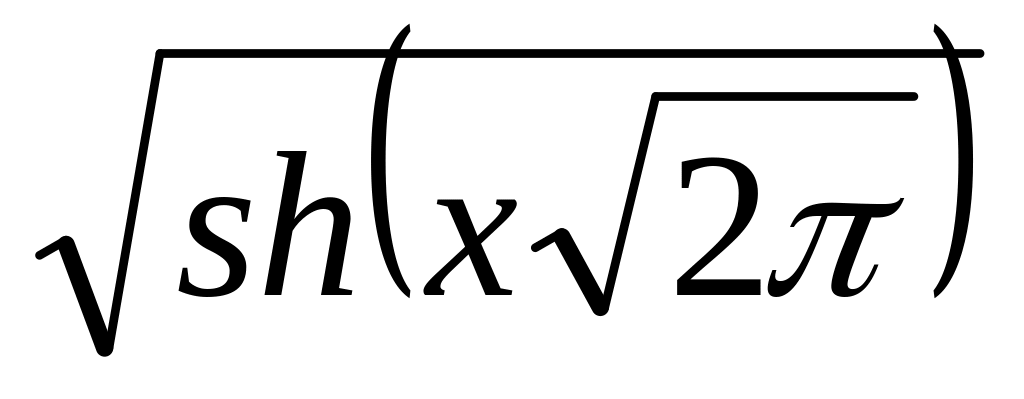
1.50
2.22
10-8
12
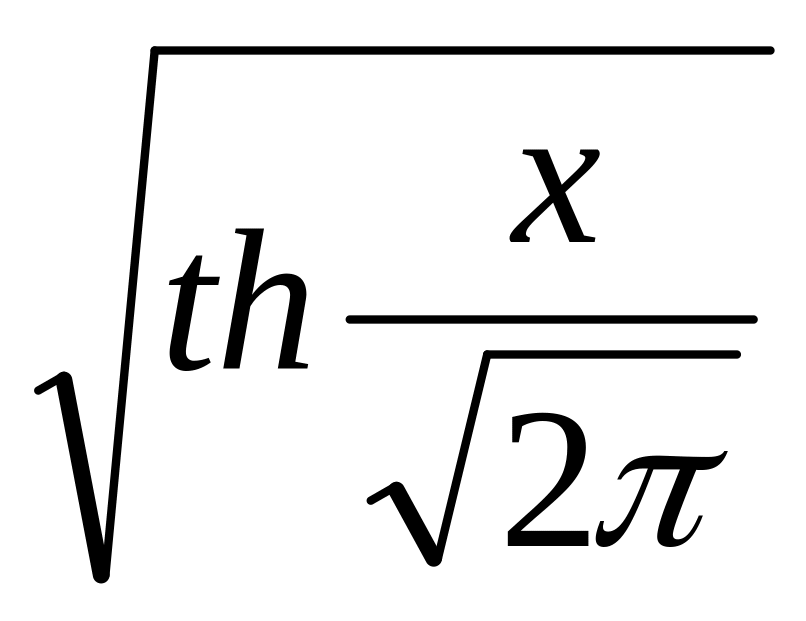
0.5
1.7
10-8
13
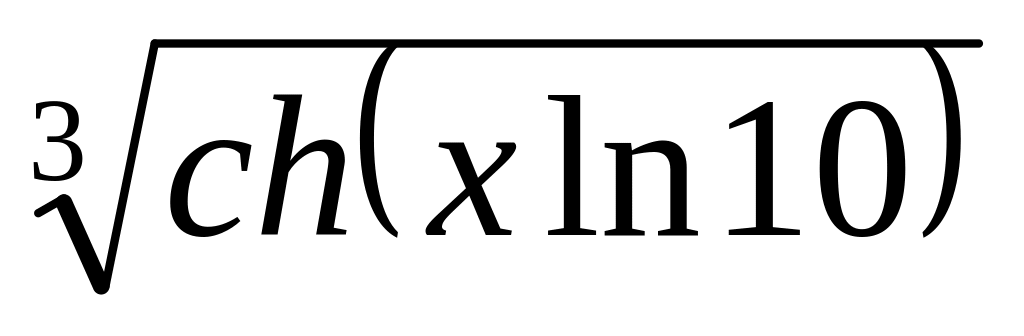
1.5
3.1
10-8
14
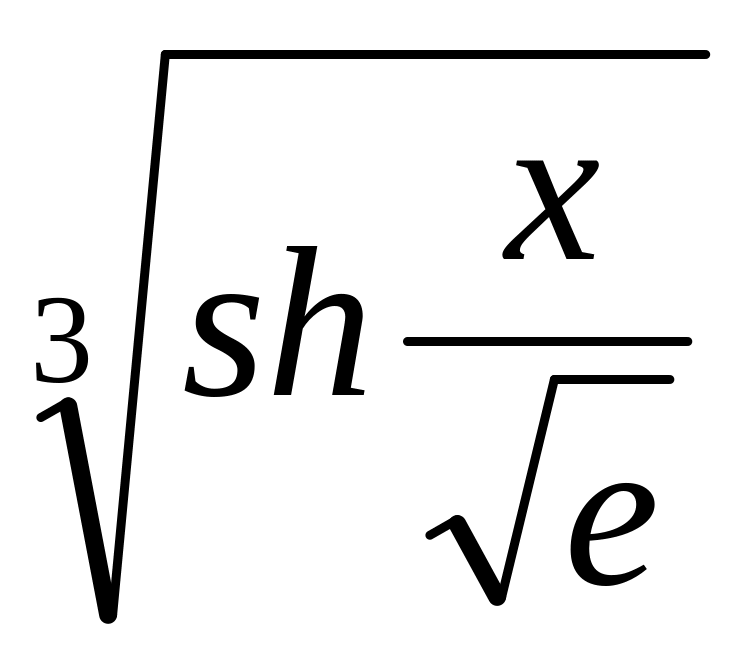
2
6
10-8
15
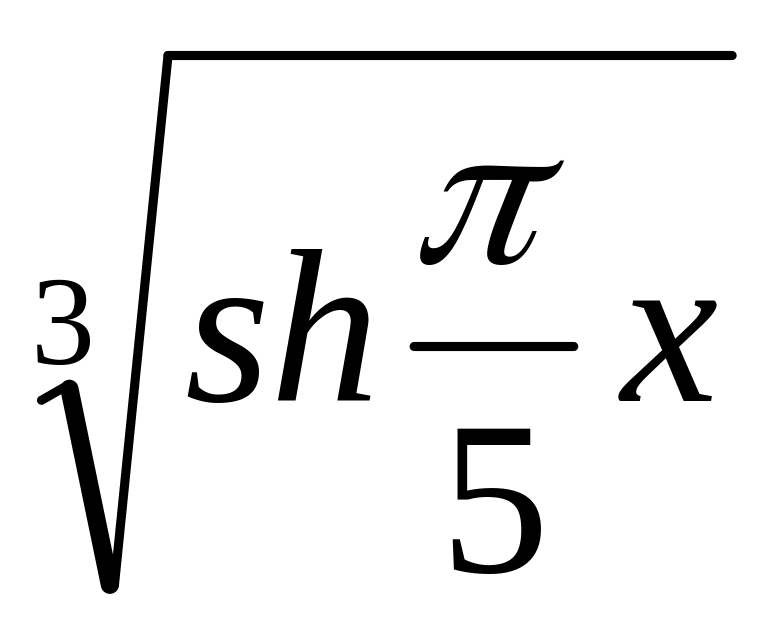
2.0
5.2
10-8
16
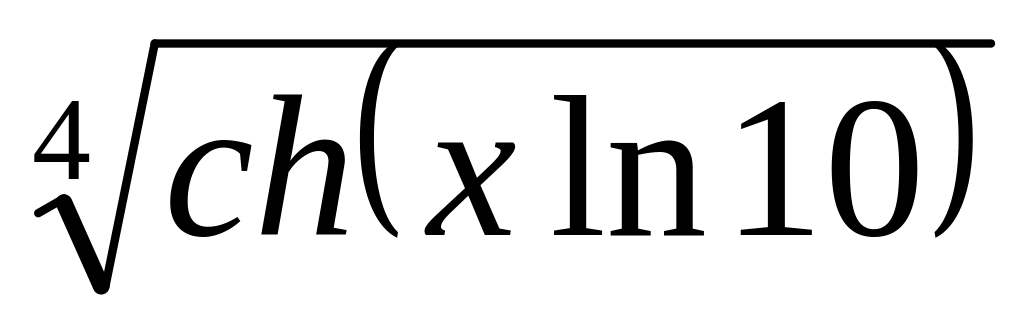
1.5
3.1
10-8
17
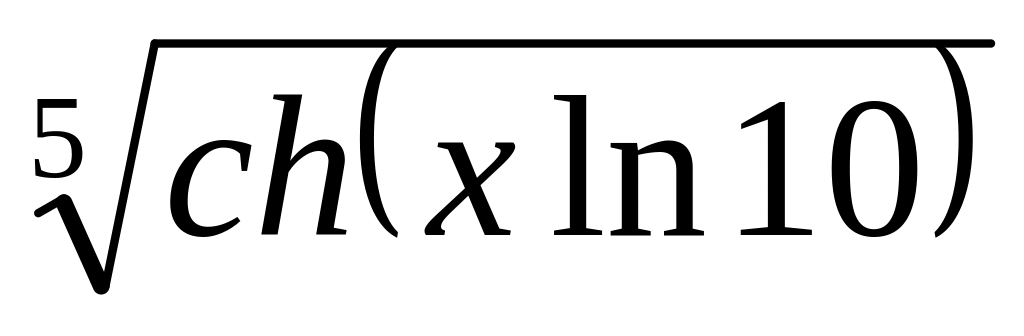
1.5
3.1
10-8
18

2.0
6.0
10-8
№
f(x)
a
b
19
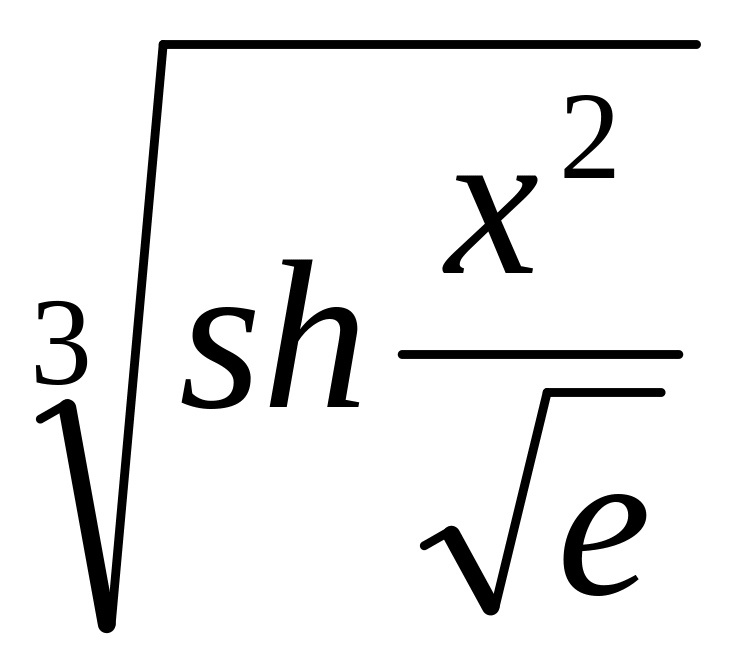
2
6
10-8
20
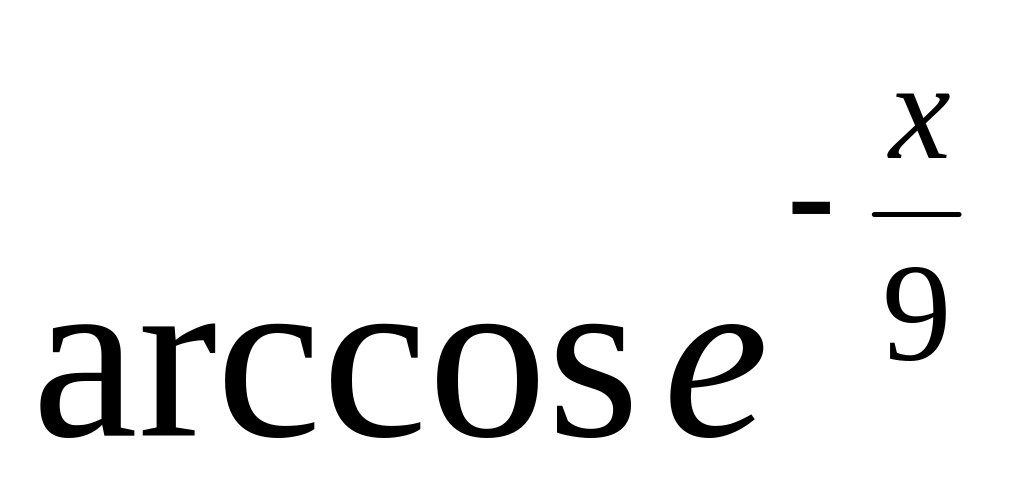
2.2
7.0
10-8
21
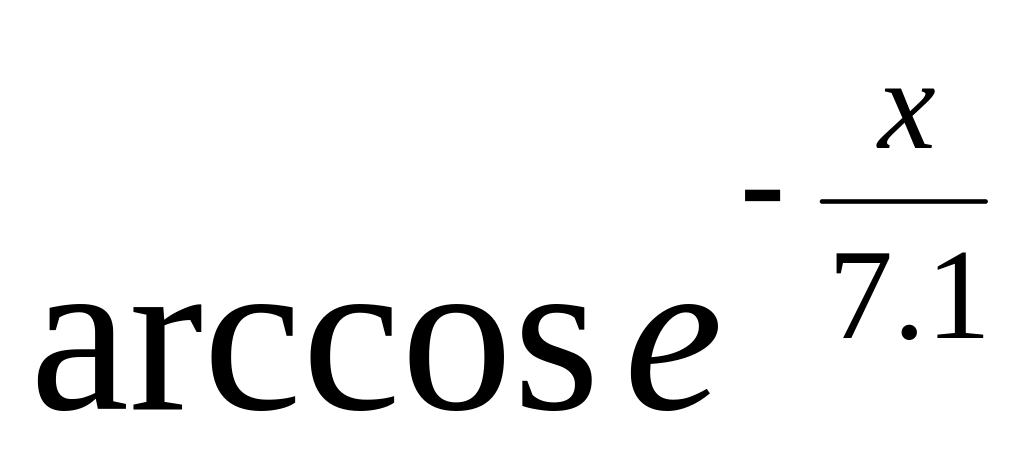
2.21
7.01
10-8
Квадратурами прямоугольников, трапеций и Симпсона вычислить интегралы с заданной точностью. Пояснить, почему получается такое число подинтервалов?
Построить таблицу значений интеграла
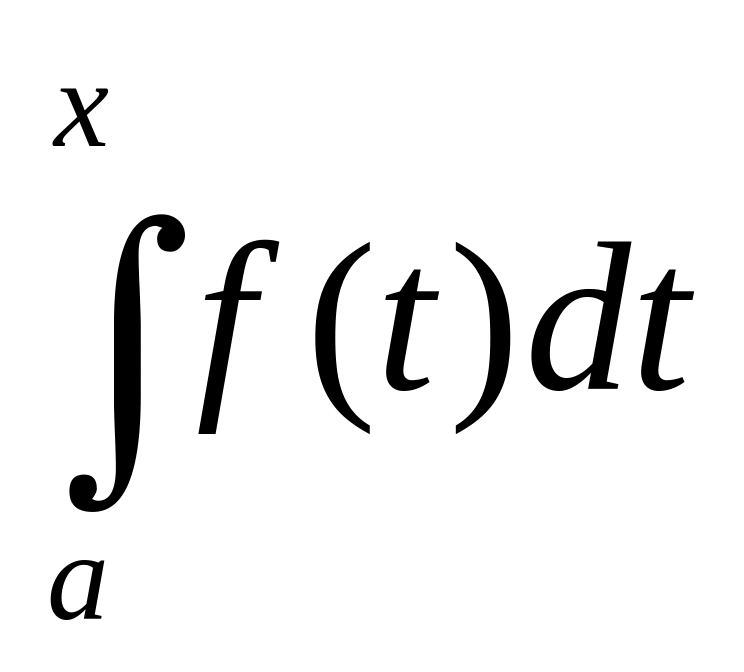 ,
где
,
где
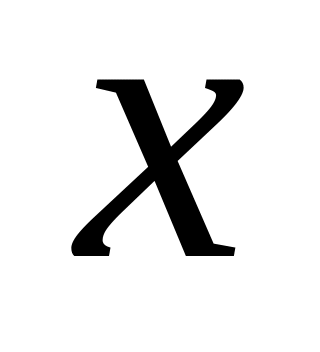 принимает десять значений из промежутка
принимает десять значений из промежутка
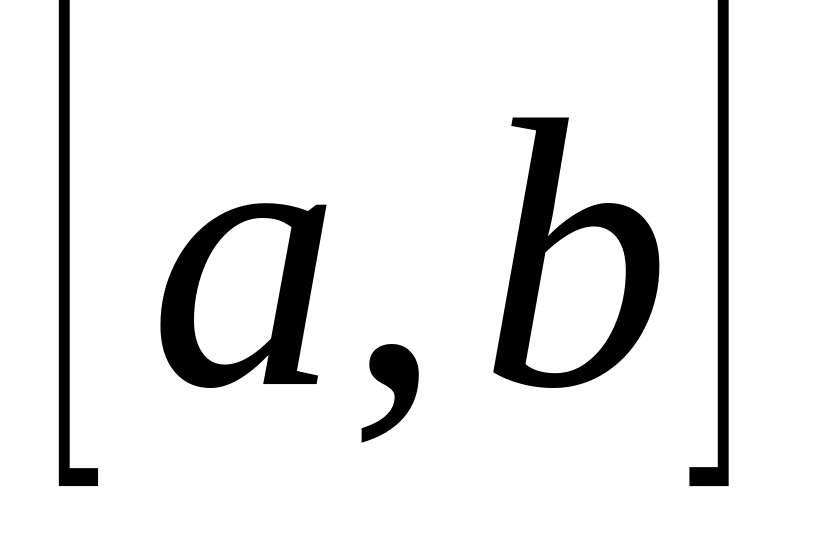 ,
допускающую линейную интерполяцию.
Результат должен быть представлен со
всеми верными цифрами.
,
допускающую линейную интерполяцию.
Результат должен быть представлен со
всеми верными цифрами.
Контрольные вопросы к лабораторной работе.
