
- •Лабораторная работа №5. Решение систем линейных уравнений.
- •Часть 1.
- •Содержание.
- •5.1 Метод Гаусса.
- •5.2 Погрешность решения системы. Нормы матриц. Обусловленность систем.
- •5.3 Итерационное уточнение решения линейной системы.
- •Задачи для самостоятельного решения.
- •Задания к лабораторной работе.
- •Приложение 1. Вычисление нормы матрицы согласованной с евклидовой нормой вектора.
- •Литература.
5.3 Итерационное уточнение решения линейной системы.
Несмотря
на то, что ошибки округления, как правило,
невелики, иногда возникает необходимость
получить решение с более высокой
точностью. Ключом для улучшения точности
первого решения
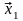 является вычисление с двойной точностью
его невязки
является вычисление с двойной точностью
его невязки
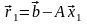 .
Зная
.
Зная
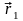 ,
мы затем решаем систему
,
мы затем решаем систему
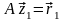 .
.
Если
мы знаем
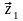 точно, то
точно, то
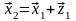 будет точным решением системы, потому
что
будет точным решением системы, потому
что
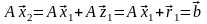 .
.
Если
мы не знаем
точно, то можно вычислить
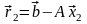 и продолжить процесс уточнения решения:
зная
и продолжить процесс уточнения решения:
зная
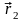 ,
мы затем решаем систему
,
мы затем решаем систему
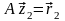 .
.
Заметим,
что каждая система
 имеет ту же матрицу
и поэтому прямой ход метода Гаусса можно
выполнить лишь один раз, если мы представим
его в виде умножения на некоторую матрицу
.
Если не производить выбор ведущего
элемента, то
имеет ту же матрицу
и поэтому прямой ход метода Гаусса можно
выполнить лишь один раз, если мы представим
его в виде умножения на некоторую матрицу
.
Если не производить выбор ведущего
элемента, то
 .
.
Как
нетрудно видеть перестановку
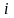 -той
и
-той
и
 -той
строк можно свести к умножению на матрицу
-той
строк можно свести к умножению на матрицу
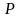 у которой по диагонали, за исключением
этих строк, стоят единицы, а в
-той
строке на
-том
месте стоит единица и в
-той
строке на
-том
месте стоит единица, другие элементы
этой матрицы равны нулю. С учетом этого
обстоятельства матрицу
можно записать в виде:
у которой по диагонали, за исключением
этих строк, стоят единицы, а в
-той
строке на
-том
месте стоит единица и в
-той
строке на
-том
месте стоит единица, другие элементы
этой матрицы равны нулю. С учетом этого
обстоятельства матрицу
можно записать в виде:
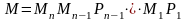 .
.
Исключительно
важно, чтобы вычисление невязок
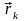 выполнялось с более высокой точностью,
чем остальные операции. Это
основной принцип для любых способов
решения уравнения: вычисление невязки
является критической операцией, и должно
выполнятся точнее других операций.
выполнялось с более высокой точностью,
чем остальные операции. Это
основной принцип для любых способов
решения уравнения: вычисление невязки
является критической операцией, и должно
выполнятся точнее других операций.
Детальный
анализ ошибок округления дан в предыдущем
параграфе, сходимость процесса
итерационного уточнения решения мы
рассмотрим чуть позже, а сейчас дадим
некоторое правдоподобное представление
о природе алгоритма. В частности, мы
покажем, что величина
приближенно определяет быстроту
сходимости
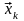 к своему предельному вектору. Обратно,
последовательность
может быть использована для оценки
величины
.
к своему предельному вектору. Обратно,
последовательность
может быть использована для оценки
величины
.
Замечание.
Ошибка
 решения системы
связана с
простым соотношением
решения системы
связана с
простым соотношением
 ,
таким образом
,
таким образом
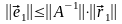 .
.
По результатам предыдущего параграфа имеем
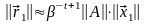 .
.
Используя предыдущее равенство и замечание, имеем:
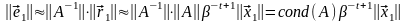 .
.
Следовательно,
при
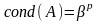
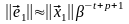 .
.
Если
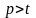 ,
то можно положить
,
то можно положить
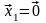 ,
в другом случае
,
в другом случае
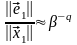 ,
,
т.
е. у
приблизительно
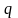 первых разрядов верны, а остальные в
пределах погрешности.
первых разрядов верны, а остальные в
пределах погрешности.
После
вычисления
,
мы можем предположить, что невязка имеет
-
верных разрядов. Когда мы решаем систему
уравнений для
,
то получим еще
-
верных разрядов. Следовательно,
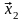 имеет
имеет
 верных разрядов.
верных разрядов.
Задачи для самостоятельного решения.
№1.
Доказать,
имеет место неравенство
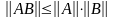 .
.
№2.
Доказать, что имеют место равенства:
а) ,
б) ,
где нормы матриц согласованы с соответствующими нормами векторов.
№3.
Пусть
и
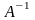 имеют следующий вид:
имеют следующий вид:
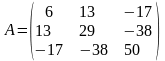 ,
,
 .
.
Собственные значения матрицы приближенно равны 0.0558, 0.2007, 84.74.
а)
Описать множество
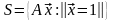 ,
т.е. образ единичной сферы при преобразовании
.
,
т.е. образ единичной сферы при преобразовании
.
б)
Найти
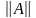 ,
,
 ,
.
,
.
в) Рассмотрим систему уравнений . Предположим, что мы имеем векторы и , относительно которых известно только, что
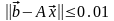 .
.
1)
Какова наименьшая верхняя граница для
абсолютной ошибки
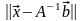 .
.
2)
Какова наименьшая верхняя граница для
относительной ошибки
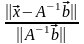 .
.
№4.
Пусть
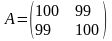 .
.
Доказать,
что данная матрица имеет наибольшее
число обусловленности
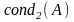 8
из всех невырожденных матриц второго
порядка, элементами которых являются
положительные числа меньшие или равные
100.
8
из всех невырожденных матриц второго
порядка, элементами которых являются
положительные числа меньшие или равные
100.
№ 5.
Пусть
симметричная положительно определенная
матрица. Доказать, что
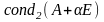 есть монотонно убывающая функция
есть монотонно убывающая функция
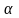 ,
при
,
при
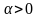 .
.
№ 6.
Найти евклидову норму диагональной матрицы.
№ 7.
Найти евклидову норму ортогональной матрицы.
№ 8.
Показать,
что на основании следующего алгоритма
можно получить оценку числа обусловленности
матрицы, по норме, согласованной с
векторной
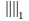 .
Для расчета
,
находят вектора
.
Для расчета
,
находят вектора
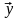 и
и
 ,
для этого решаются две системы уравнений
,
для этого решаются две системы уравнений
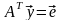 ,
,
 ,
,
где
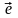 -
вектор с компонентами
-
вектор с компонентами
 ,
выбираемый так, чтобы максимизировать
,
выбираемый так, чтобы максимизировать
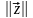 в процессе обратной подстановки для
,
причем
в процессе обратной подстановки для
,
причем
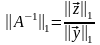 .
.
