Розділ 3 кручення стрижня круглого попереччя

3.1 Загальні відомості

Циліндричний брус, закріплений одним кінцем і навантажений парою сил з моментом М₁, що діє в площині поперечного перерізу, зазнає деформації кручення. При цьому крутний момент М_К у будь-якому перерізі циліндра, що є моментом внутрішніх сил пружності, чисельно дорівнює моменту зовнішньої пари сил, що діє на будь-яку сторону від перерізу, тобто

. (3.1)

Розгляд випадку, коли на циліндр діє декілька моментів різного напряму (наприклад, це ведучий вал редуктора з урівноваженим ступенем), показує, що крутний момент у будь-якому перерізі валу чисельно дорівнює алгебраїчній сумі зовнішніх моментів, що діють зліва або праворуч від даного перерізу в площинах, перпендикулярних до осі валу, тобто

.

3.2 Розрахунки на міцність і жорсткість стрижнів при крученні

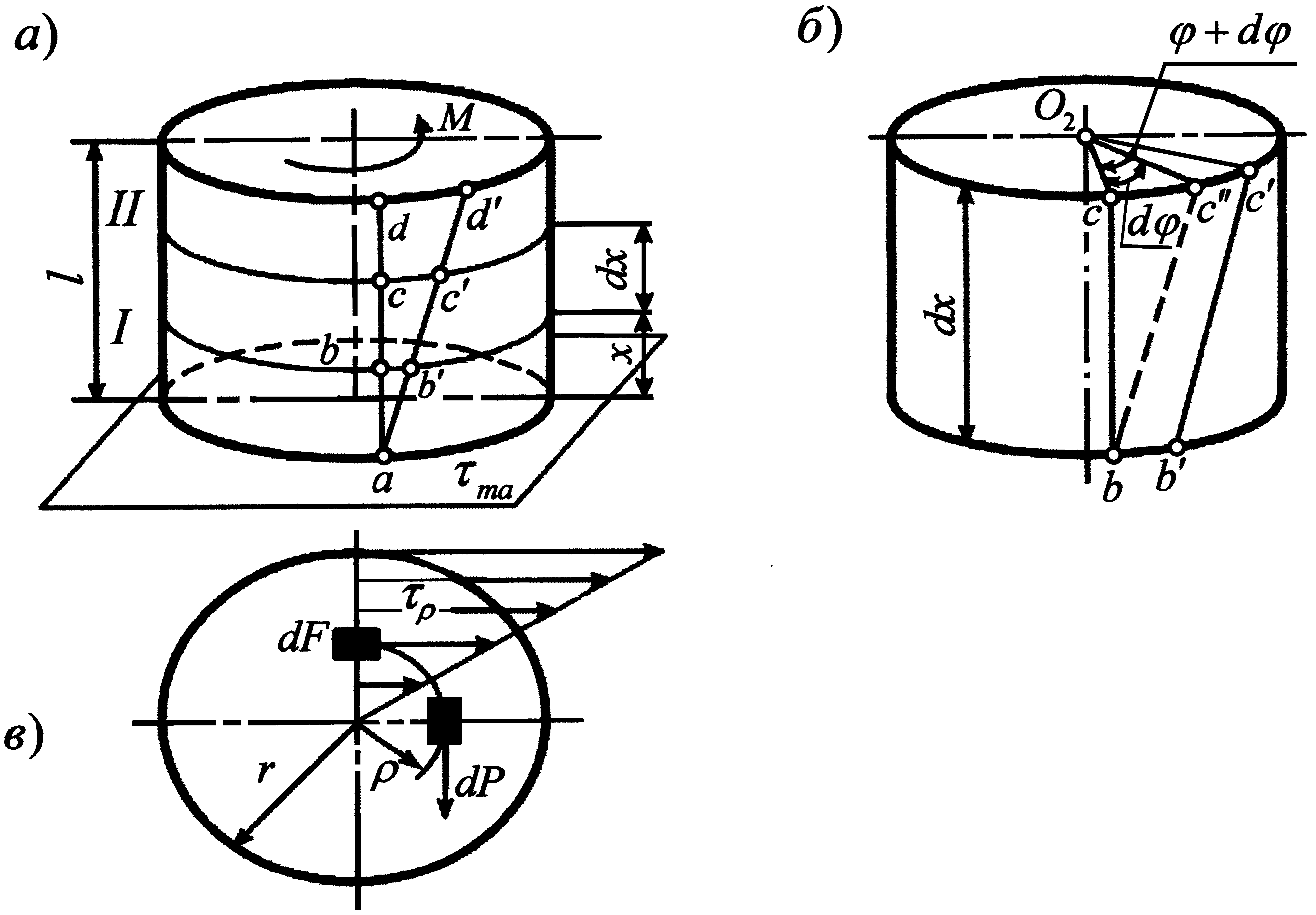
Рисунок 3.1 До умов міцності і жорсткості стрижнів при крученні

Розглянемо елемент циліндру, виділений перерізами I і II, кінець якого закріплений нерухомо на вказаній площині, а інший навантажений парою сил з моментом М (рисунок 3.1, а). В результаті дії зовнішнього моменту М виникає деформація кручення, при якій твірна циліндра adcd займе положення abcd (рисунок 3.1, а).

Якщо переріз I–I, що знаходиться на відстані х від нижнього кінця циліндра, обернувся на кут , то переріз II–II, що знаходиться на відстані від нижнього перерізу, обернеться на кут (рисунок 3.1, б). Проведемо з точки b пряму bс паралельно до прямої bс. Тоді кут  сО₂с = d. Елемент bссb до повороту перерізу II щодо перерізу I мав вертикальні бічні сторони, отже, абсолютний зсув елементу: .

Відносний зсув визначається з виразу:

.

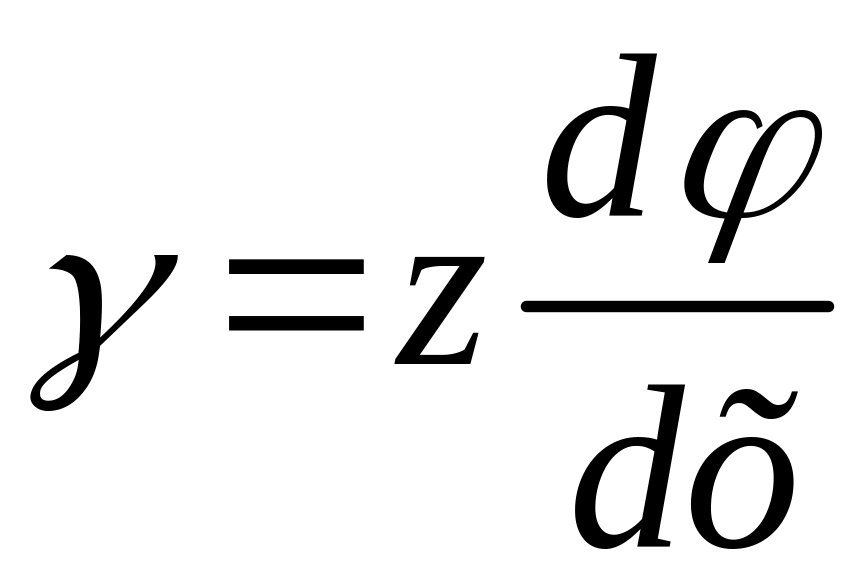Позначимо 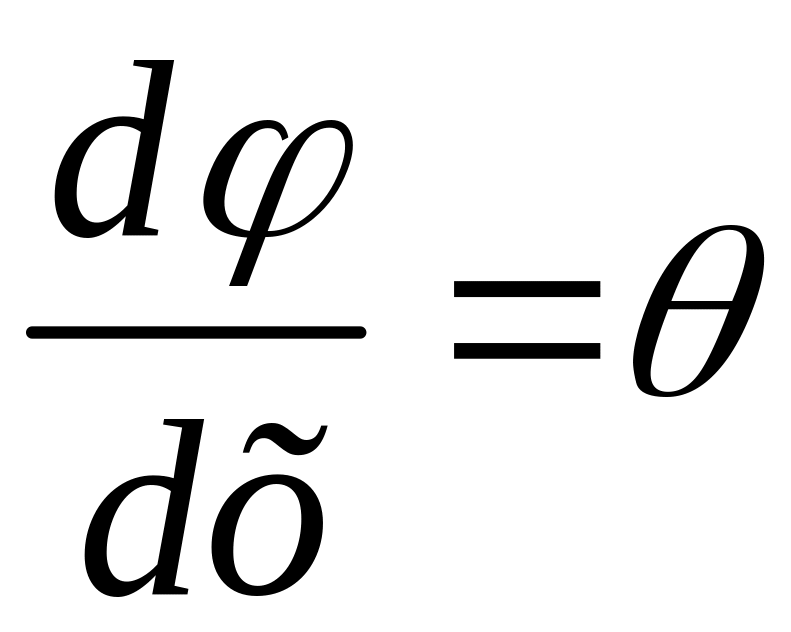, тоді , де – кут закруту, віднесений до одиниці довжини циліндра, називають відносним кутом закруту.

Для циліндрів постійного перерізу, на які діє крутний момент, . Оскільки відповідно до прийнятих допущень радіуси при крученні залишаються прямими, то можна сказати, що для всякого елементу, що розташований усередині циліндра на радіусі відносний зсув визначається за виразом:

. (3.2)

За законом Гукa напруга в перерізі циліндра визначається з виразу:

(3.3)

при ; .

Із співвідношення (3.3) виходить, що напруга усередині циліндра змінюється за лінійним законом пропорційно відстані від осі обертання. Мінімальна напруга, що дорівнює нулю, має місце в центрі поперечного перерізу, а максимальне – на поверхні циліндра (рисунок 3.1, в).

Елементарна дотична сила, перпендикулярна до радіусу перерізу, проведеному до центру тяжіння елементарної площинки dF, що діє на неї, з урахуванням співвідношення (3.3), визначається з виразу:

.

Елементарний момент, що створюється силою щодо центру перерізу визначається з виразу:

.

Сума таких елементарних моментів, узята за всією площею поперечного перерізу циліндра, дорівнює крутному моменту , який діє в даному перерізі циліндра і в даному конкретному випадку дорівнює зовнішньому моменту М:

.

Оскільки і , то

.

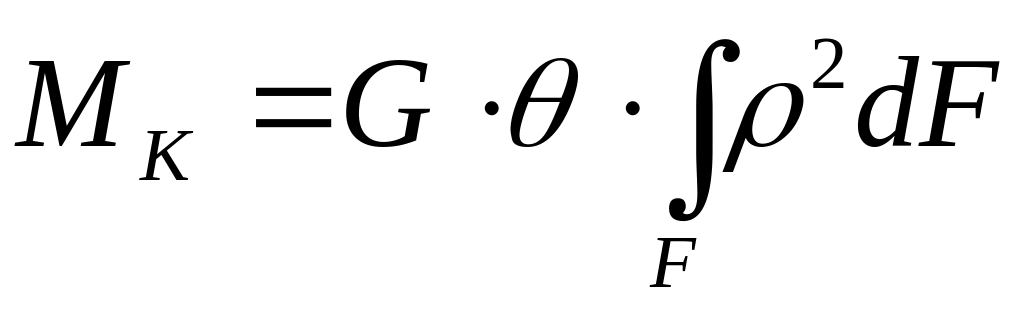Але 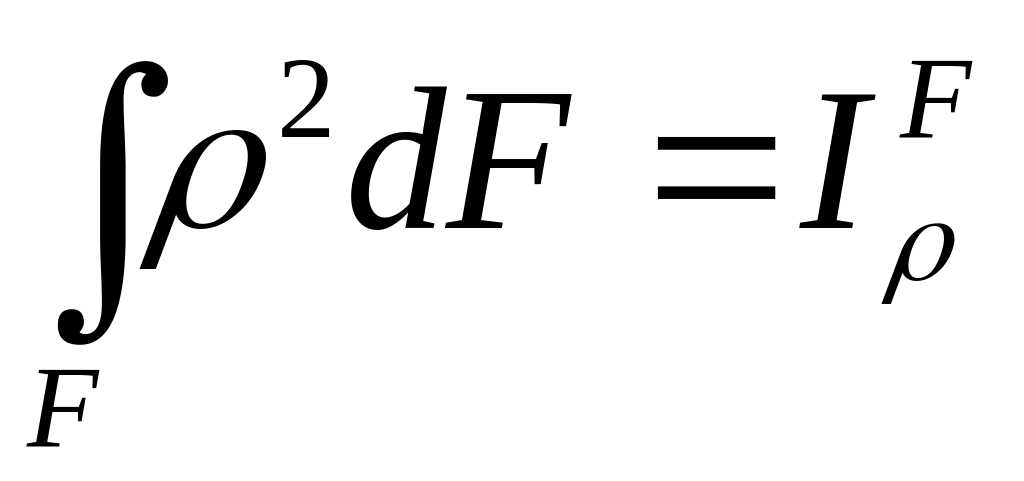– полярний момент інерції площі, тому:

. (3.4)

Із співвідношення (3.4) отримаємо величину кута закруту, віднесеного до одиниці довжина циліндра:

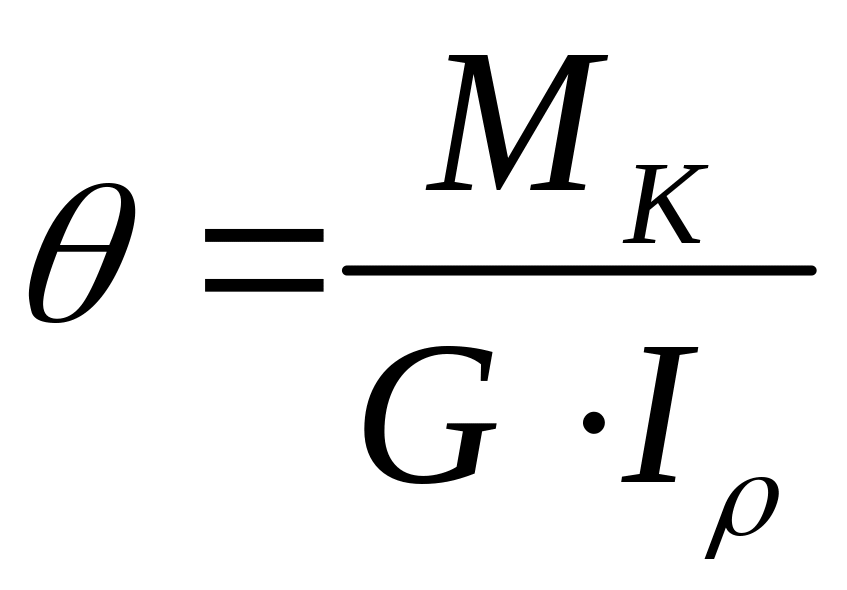. (3.5)

Повний кут закруту в радіанах:

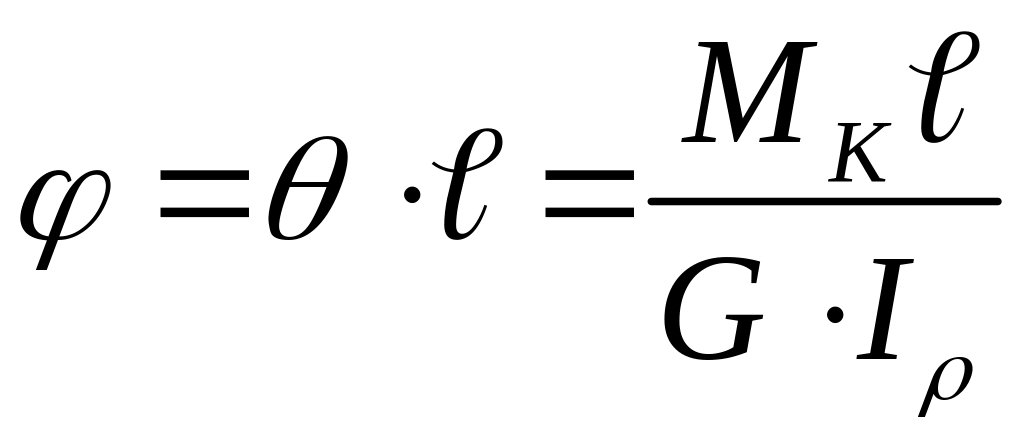, (3.6)

або в градусах:

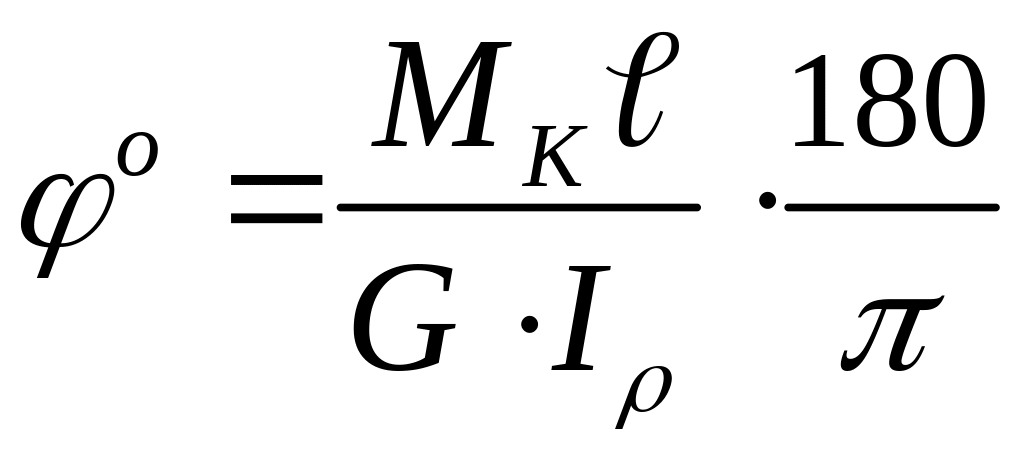(3.7)

Добуток модуля пружності другого роду на полярний момент інерції називають жорсткістю при крученні. Ця величина характеризує здатність тіла з даного матеріалу з поперечним перерізом даного розміру і форми чинити опір деформації кручення. Таким чином, повний кут закруту циліндра прямо пропорційний крутному моменту і довжині циліндра і обернено пропорційний жорсткості при крученні.

Знайдемо залежність напруги від крутного моменту. Відповідно до (3.3) замість підставляємо його значення з (3.5):

.

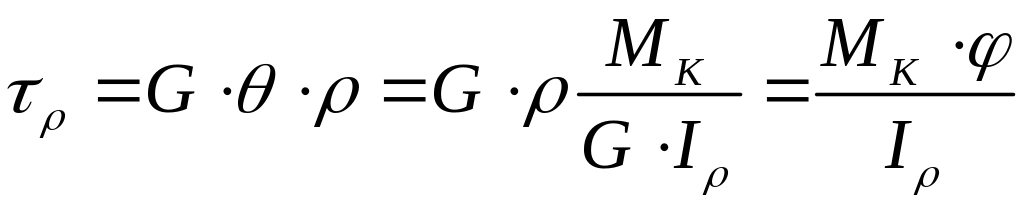Звідси (рисунок 3.1, в) найбільша напруга при крученні:

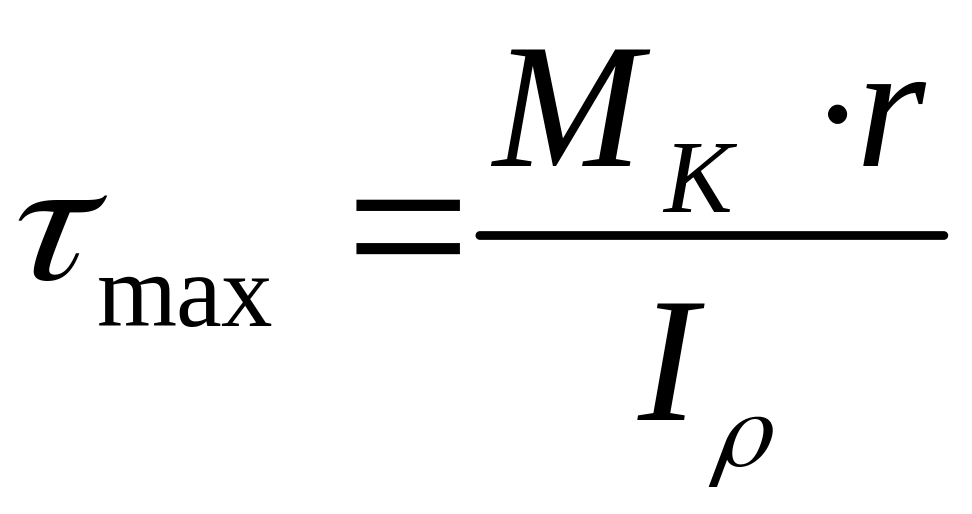, (3.8)

або

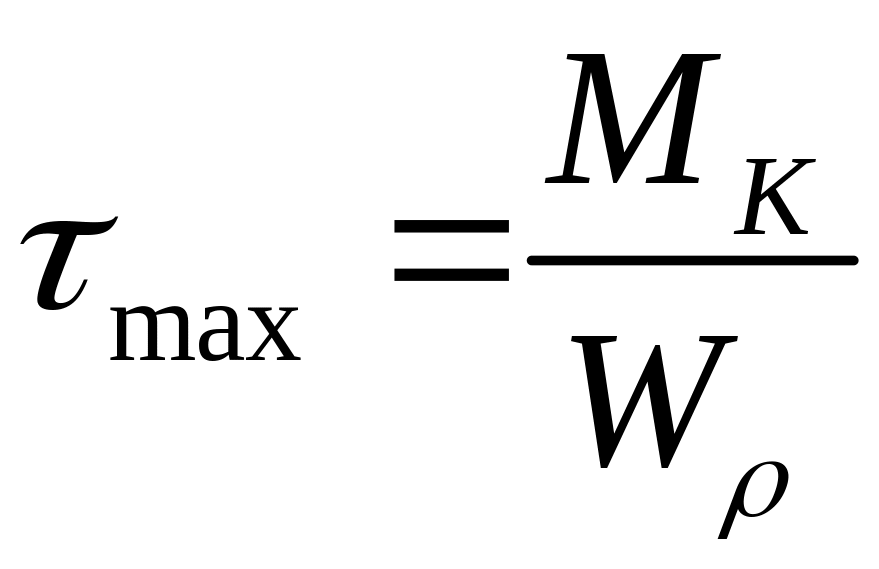, (3.9)

де 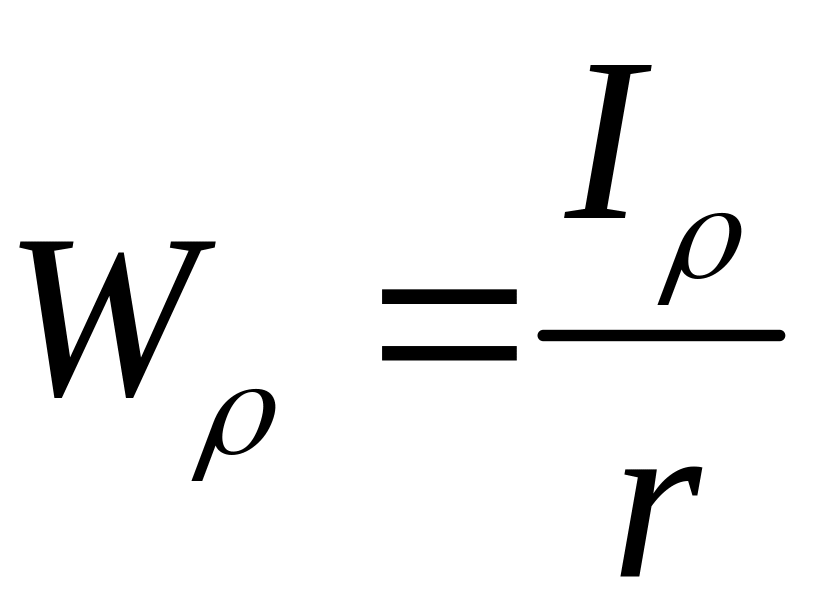– відношення полярного моменту інерції до відстані від осі обертання до найбільш віддаленої точки перерізу; це відношення називають полярним моментом опору.

Умова міцності при крученні буде виконаються в тому випадку, якщо максимальне значення напруги, що виникає при крученні, не перевищує величини напруги, що допускається, тобто рівняння міцності при крученні має вигляд:

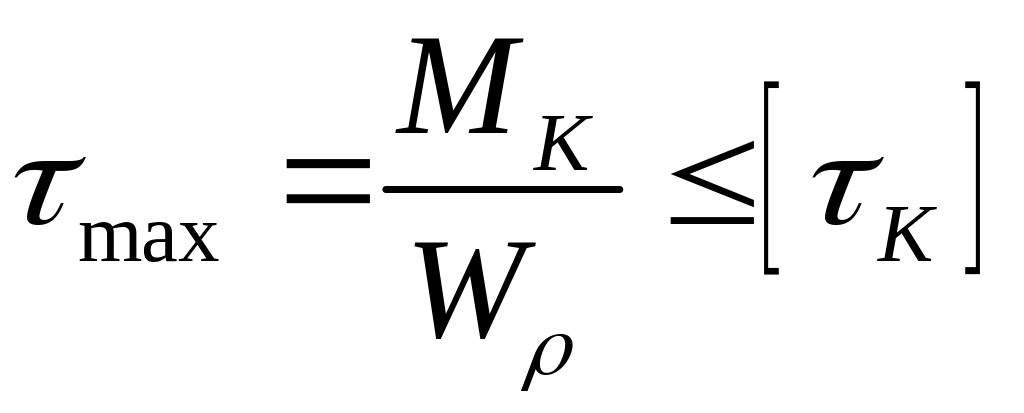. (3.10)

Допускну напругу при крученні для сталі зазвичай приймають:

,

де – допускна напруга при розтягуванні.

Наведемо співвідношення для визначення полярного моменту опору:

 для круга діаметром d з урахуванням виразу (3.4):

;

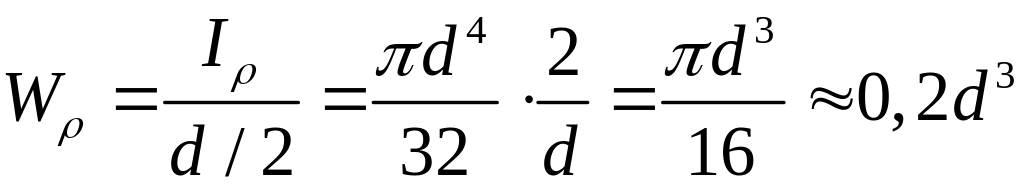 для кільця, з урахуванням співвідношення (3.5):

,

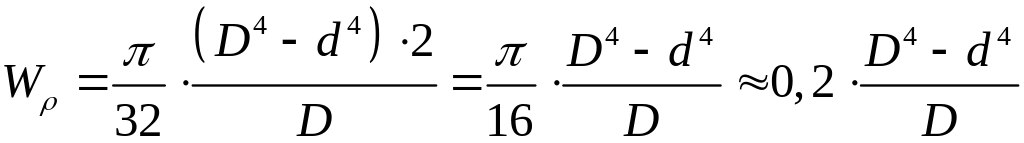де D – зовнішній і – внутрішній діаметр кільця.

При 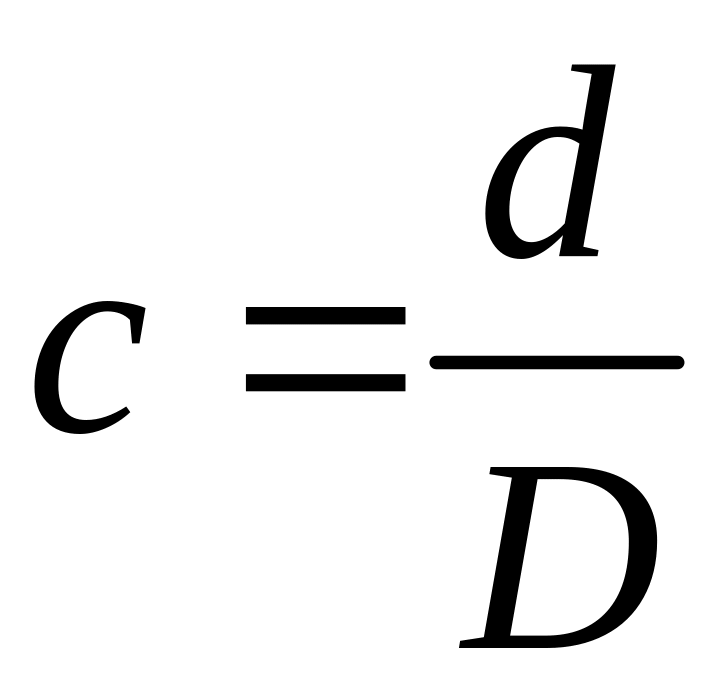полярний момент опору кільця:

.

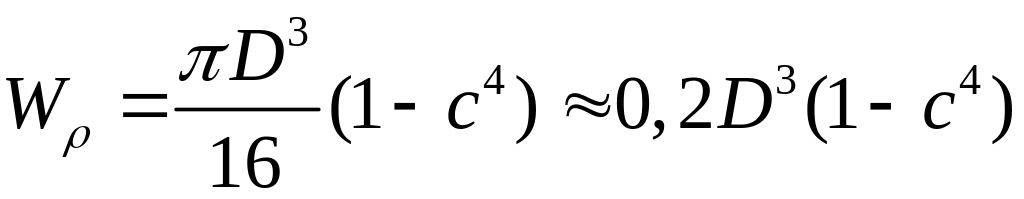До раніше наведеному рівнянню (3.11) міцності при перевірочному розрахунку встановимо рівняння міцності при проектувальному розрахунку, коли необхідно визначити параметри циліндру (зокрема, діаметр валу) при крученні.

Визначити діаметр циліндру , що зазнає деформацію кручення, можна використовуючи два припущення. У тих випадках, коли визначною є міцність циліндру, розрахунок ведуть за виразом (3.10) для суцільного циліндру:

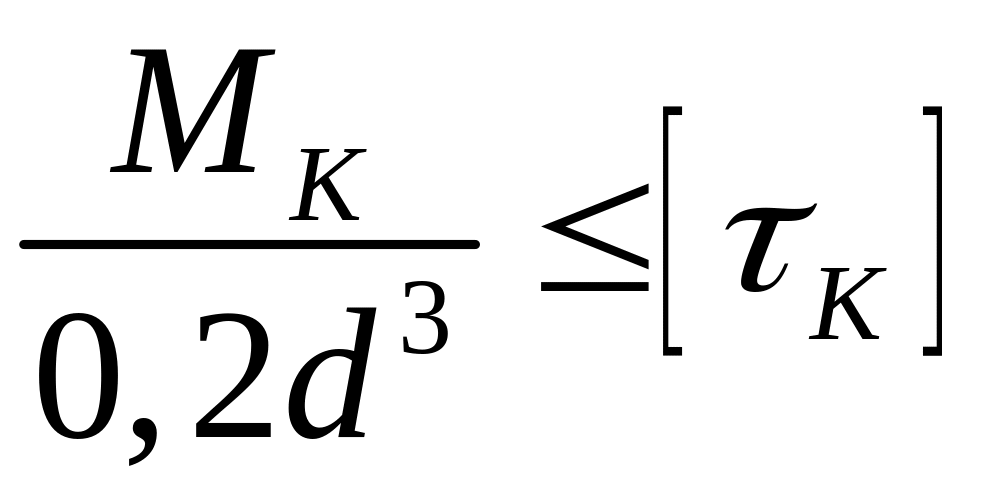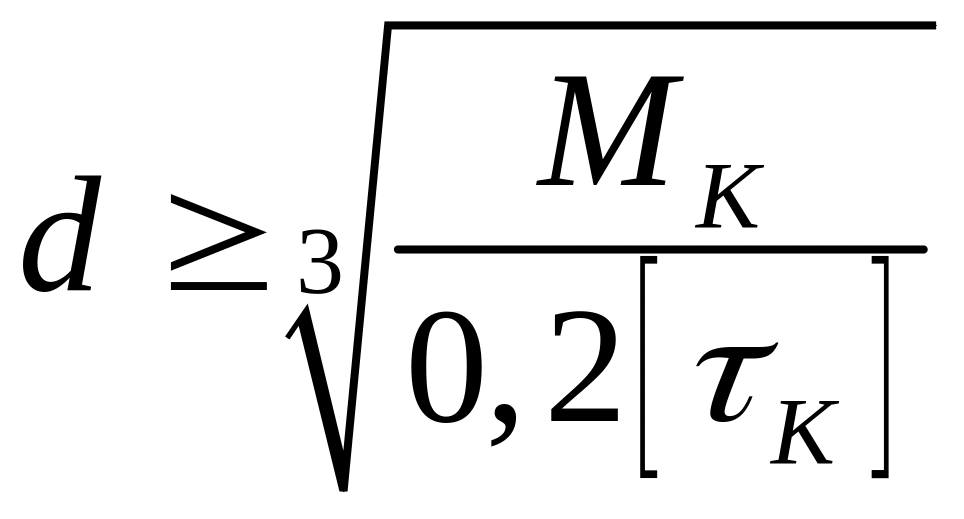; . (3.11)

Коли визначальним є гранична деформація (кут закруту), розрахунок ведуть на жорсткість. З рівняння (3.7) маємо:

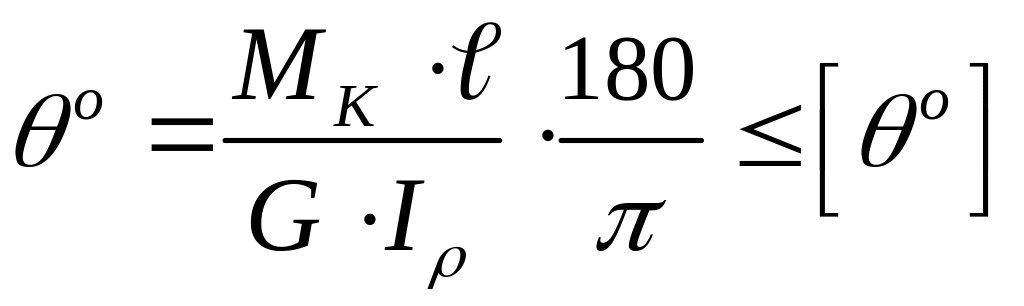, (3.12)

де – допускний кут закруту на одиницю довжини, який залежно від призначення валу приймають в межах 0,25 . . . 1,0 град/м;

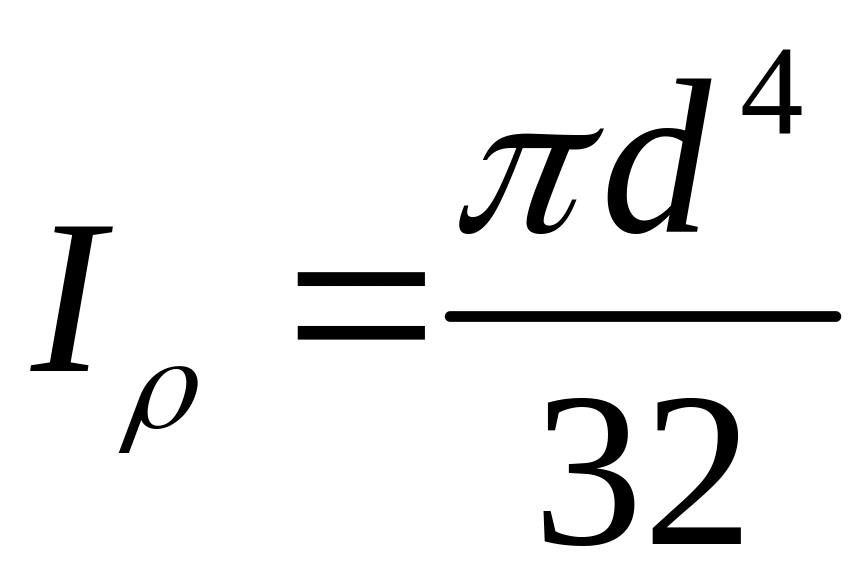– полярний момент інерції суцільного циліндру.

Тоді діаметр валу суцільного перерізу на підставі рівняння жорсткості дорівнюватиме :

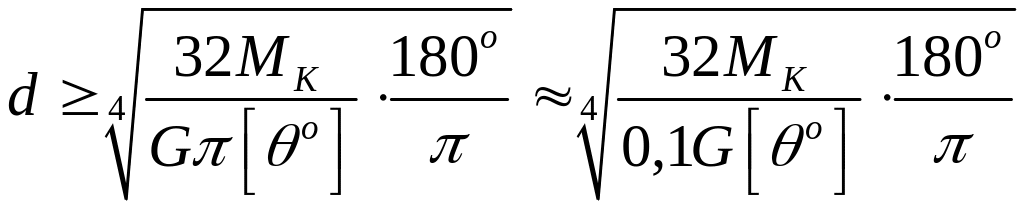. (3.13)

Користуючись рівняннями (3.10) і (3.12), можна вирішити і іншу задачу: визначити безпечну величину крутного моменту бруса, при якому забезпечується необхідна міцність або жорсткість.

Таким чином, за двома видами напруженого стану – гнутті й крученні визначають основний параметр, що впливає на величину напруги – момент, з метою з'ясування, чи виконується умова міцності і чи лінійні і кутові параметри деформації відповідають допускним.

Запитання для самоперевірки

1 Яке деформування тіла називають крученням? Що таке закручувальний момент?

2 Що таке зсув? Наведіть приклади роботи елементів конструкцій на зсув. Як називають руйнування при зсуві?

3 Яка існує в'язь між напругами і деформаціями при чистому зсуві? За якого обтягу прямий стрижень зазнає кручення?

4 Сформулюйте вихідні передумови теорії кручення прямого стрижня кругло­го попереччя.

5 Які напруги виникають в поперечному перерізі круглого стрижня при кру­ченні?

6 Чи виникають при крученні круглого стрижня нормальні напруги?

7 Напишіть формулу для напруг при крученні круглого стрижня.

8 Напишіть формули для відносного і повного кута закруту круглого стрижня.

9 Що називають жорсткістю попереччя при крученні?

10 Напишіть вирази полярних моментів інерції круглого попереччя (суцільного і кільцевого).

11 Що називають полярним моментом опору і чому він дорівнює для круга і кільця?

12 Чим пояснити, що стрижень кільцевого попереччя при крученні економіч­ніший, ніж суцільного ?

13 Запишіть умову міцності при крученні.