Упражнение 1 Определение радиуса кривизны линзы

1.Установите источник света перед конусной насадкой опак-иллюминатора. Подайте с помощью автотрансформатора такое напряжение на лампу, чтобы ток, проходящий через лампу, был около 2 ампер. По мере вхождения в режим ток лампы будет падать. Ток при установившемся режиме (5-7 мин) равен 1,2 А. При меньшем токе лампа может погаснуть, поэтому необходимо некоторое время поддерживать трансформатором ток не ниже и не выше 1,1 – 1,2 А, а затем приступить к выполнению лабораторной работы.

2. Поместив линзу на стеклянную пластинку, устанавливают последнюю так, чтобы точка соприкосновения линзы с пластиной попала точно в поле зрения микроскопа. При этом образующиеся на границе воздушного слоя линзы кольца Ньютона должны быть отчетливо видны. Если этого не будет, то, не снимая линзы, исправляют фокусировку микроскопа. Если в точке соприкосновения вместо темного пятна получится светлое, то это значит, что между поверхностями линзы и стекла имеются пылинки. Необходимо линзу и пластинку протереть мягкой салфеткой.

3. Установить биштрих на середину шкалы окулярного микрометра. Центральное пятно (первое кольцо) установить на перекрестье. Вращая микрометрический винт, устанавливают перекрестье на 20-ое темное кольцо справа и производят отсчет по шкале (мм) и барабану (сотые доли мм) окулярного микрометра. После этого вращая микровинт, устанавливают перекрестье на 19-ое, 18-ое и т. д. До 5-ого включительно и производят отсчет. Затем перемещают перекрестье через центр до 5-ого кольца слева и проделывают те же измерения по 20-ое кольцо включительно.

4. Вычитая из отсчетов, полученных справа, отсчеты, полученные слева, определяют диаметры, а затем и радиусы колец, по формуле (7) определяют радиус кривизны линзы. При этом в целях повышения точности результатов рекомендуется комбинировать радиус кольца номер К с радиусом кольца номер К/2; кольца (К-1) с (К/2-1) и т. д. Из полученных величин берут среднее арифметическое.

Измерения в данном упражнении провести с установленным зеленым светофильтром, длина волны которого λ =5460 Å.

Обязательно учесть, что увеличение микроскопа равно 10.

Упражнение 2 Определение длин волн линий ртути

В окно защитного колпачка лампы вставляют светофильтр, выделяющий сине-фиолетовую линию ртути. Методика измерения та же, что и в упражнении 1.

Все данные измерений и вычислений занести в таблицу.

Таблица

№ кольца	отсчет микромет- ра правый	отсчет микрометра левый	диаметр колец D	радиус колец r	Квадраты диаметров колец D2

Подставляя в формулу (7) значение радиуса кривизны линзы, найденное в упражнении 1, определяют длину волны выделенной ртутной линии.

Можно определить длину волны линий ртути графическим методом. Для этого необходимо посчитать квадраты диаметров измеренных колец и занести в таблицу. Построить график, откладывая по оси ординат квадрат диаметров, а по оси абсцисс – номера колец. График должен быть прямой линией. Длина волны определяется по тангенсу угла наклона прямой к оси абсцисс.

,

где R – радиус кривизны линзы. Если известна длина волны, то таким же образом находится радиус кривизны линзы.

ВОПРОСЫ ПО ТЕМЕ.

1. Нарисуйте схему получения колец Ньютона.

2. Выведите формулу для радиуса m-ого кольца Ньютона (светлого).

3. Покажите лучи, создающие кольца Ньютона в отраженном свете.

4. Покажите лучи, создающие кольца Ньютона в проходящем свете

5. Объясните необходимость добавления к разности хода лучей добавки λ/2.

6. Почему при освещении систем белым светом кольца приобретают радужную окраску?

7. Почему кольца Ньютона исчезают при увеличении расстояния между линзой и пластинкой?

8. Что наблюдается в центре колец Ньютона (темное или светлое пятно), если наблюдения производятся в отраженном свете?

ЛИТЕРАТУРА.

1. Г. С. Ландсберг, Оптика, 1976, §§25-32, стр. 120-149.

2. Д. В. Сивухин, Оптика, 1980, §§33-38, стр. 228-261.

3. Ф. А. Королев, Курс физики,1974, §§15-18,стр. 85-112.

4. А. Н. Матвеев,Оптика, 1985, §29,стр. 148-161, 180-190.

5. И. В. Савельев, Курс общей физики, 1967, т. 3, §§19-20, стр. 68-75.

Лабораторная работа №7

Исследование зависимости показателя преломления растворов от их концентрации и газов от их давления интерферометром Релея

Устройство интерферометра Релея основано на дифракции Фраунгофера на двух щелях.

Пусть на экран с двумя щелями нормально падает плоская монохроматическая волна. Рассмотрим дифракционную картину Фраунгофера за экраном. Рассчитаем интенсивность световых колебаний в волне, направление распространения которой составляет угол φ с нормалью к экрану (рис. 1).

Применим для расчета принцип Гюйгенса – Френеля.

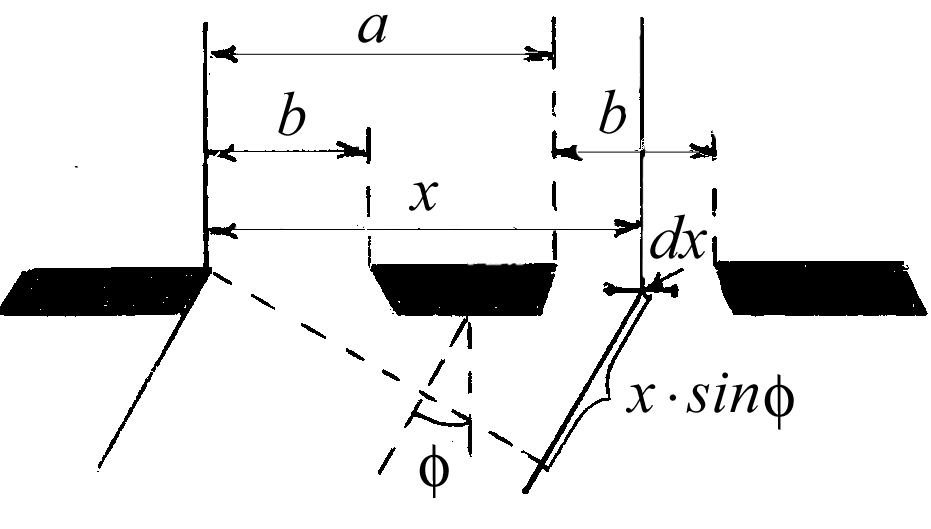
Рис. 1 .

Элемент щели dx посылает в направлении φ волну с амплитудой, пропорциональной dx. Фаза колебаний, приходящих в точку наблюдения от элемента с координатой x, отстает от колебаний, исходящих из элемента с x=0, на величину kx sinφ (k=2π/λ – волновое число). Колебание в точке наблюдения, вызванное нашим элементом, поэтому может быть написано в виде:

, (1)

где c – некоторый коэффициент пропорциональности.

Найдем результат S суммарного действия всех элементов обеих щелей. Для этого нужно проинтегрировать выражение (1) по значениям x, соответствующим открытым частям экрана.

При этом будем считать, что угол φ достаточно мал ( ) и что в правой щели создана дополнительная разность хода Δ, одинаковая для всех её элементов. Это позволяет описать смещение интерференционных полос, используемое для измерений в интерферометре Релея. Интегрируя (1), найдем:

. (2)

Элементарные вычисления дают:

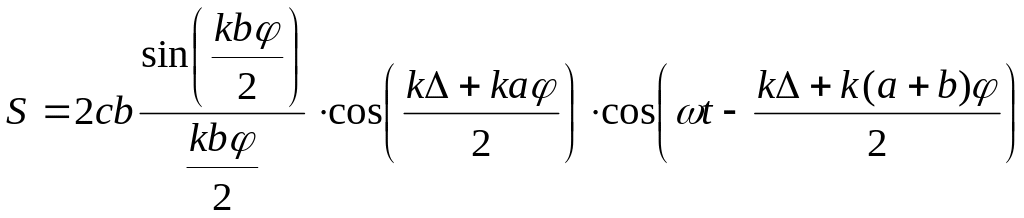. (3)

Интенсивность световых колебаний пропорциональна квадрату амплитуды:

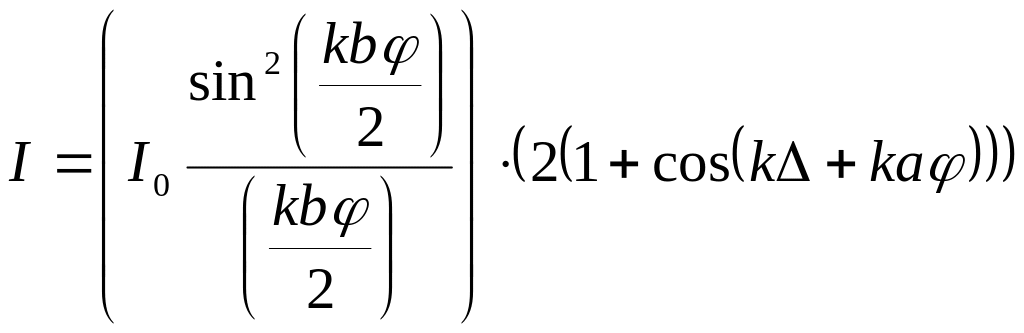. (4)

здесь I₀  c²b² – интенсивность света, возникающего в центре дифракционного пятна в том случае, когда открыта только одна из щелей.

Как видно из (4), зависимость I от φ распадается на произведение двух сомножителей. Первый из них описывает распределение интенсивности в дифракционной картине Фраунгофера от одной щели. Второй сомножитель обусловлен интерференцией световых колебаний, приходящих в точку наблюдения от разных щелей. Практический интерес представляют яркие интерференционные полосы, расположенные в пределах первого дифракционного максимума, то есть в области

.

так как углы φ и φ₀ малы и , .

Интерференционные максимумы отстоят друг от друга на расстоянии:

.

Убедиться в этом можно следующим образом: для n-го максимума , для (n+1)-го максимума . Вычитая из первого равенства второе, получим:

.

При малых углах дифракции последнее равенство можно приблизительно записать:

.

Откуда

.