
- •Дискретные случайные величины.
- •Непрерывные случайные величины.
- •Многомерные случайные величины.
- •Предельные теоремы теории вероятностей.
- •Математическая статистика.
- •Дискретные случайные величины.
- •Непрерывные случайные величины.
- •Многомерные случайные величины.
- •Предельные теоремы теории вероятностей.
- •Математическая статистика.
- •По данному распределению выборки построить эмпирическую функцию распределения, гистограмму и полигон:
- •Дискретные случайные величины.
- •Непрерывные случайные величины.
- •Многомерные случайные величины.
- •Математическая статистика.
- •По данному распределению выборки построить эмпирическую функцию распределения, гистограмму и полигон:
- •Вариант 4. Операции над событиями.
- •Классическое определение вероятности.
- •Формула сложения и умножения вероятностей. Формула полной вероятности.
- •Дискретные случайные величины.
- •Непрерывные случайные величины.
- •Многомерные случайные величины.
- •Математическая статистика.
- •По данному распределению выборки построить эмпирическую функцию распределения, гистограмму и полигон:
- •Вариант 5. Операции над событиями.
- •Формула сложения и умножения вероятностей. Формула полной вероятности.
- •Дискретные случайные величины.
- •Непрерывные случайные величины.
- •Многомерные случайные величины.
- •Предельные теоремы теории вероятностей.
- •Математическая статистика.
- •По данному распределению выборки построить эмпирическую функцию распределения, гистограмму и полигон:
Вариант 1.
Операции над событиями.
Из таблицы случайных чисел наудачу взято число. Событие А – взятое число четное, событие В – число оканчивается нулем. Что означают события: АВ,
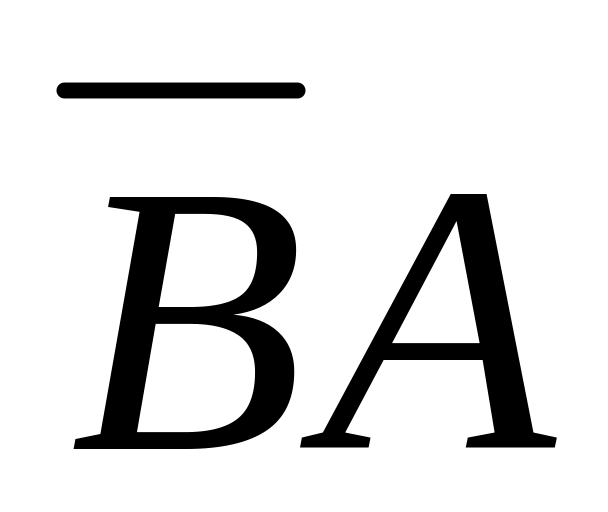 ,
,
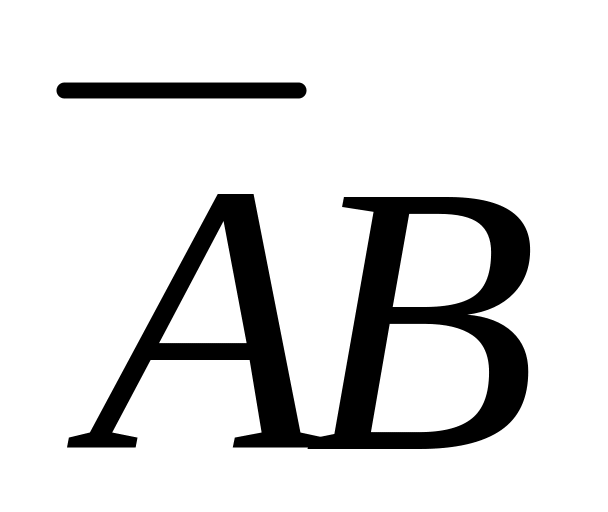 ,
А+В?
,
А+В?Рабочий изготовил 5 деталей. Пусть событие Аi, i=1,…,5, заключается в том, что i–ая изготовленная им деталь имеет дефект. Записать событие, состоящее в том, что все детали хорошие.
Классическое определение вероятности.
Из 15 билетов выигрышными являются 3. Определить вероятность того, что среди наудачу взятых 5 билетов 2 выигрышных.
Игральная кость бросается 2 раза. Найти вероятность того, что сумма очков не менее 10.
Формула сложения и умножения вероятностей.
Формула полной вероятности.
Схема Бернулли
По каналу связи передаются независимо два сообщения. Вероятность передачи без искажений первого сообщения равна 0,95, второго – 0,92. Найти вероятность того, что хотя бы одно из сообщений будет искажено.
В спортивной секции 80% студентов младших курсов и 20% старшекурсников. Среди спортсменов младших курсов разрядники составляют 20%, а среди старшекурсников – 90%. Найти вероятность того, что наудачу выбранный спортсмен окажется разрядником.
Чему равна вероятность выигрыша у равносильного соперника не менее 4 партий из 8?
Дискретные случайные величины.
Дискретная случайная величина Х задана законом распределения, представленным в таблице:
xi |
-2 |
-1 |
1 |
2 |
4 |
pi |
5/16 |
c2 |
3/8 |
c/16 |
c/16 |
1.Найти константу с. Ответ обосновать.
2.Найти математическое ожидание случайной величины Х.
3.Найти дисперсию случайной величины Х.
4.Построить график функции распределения случайной величины Х.
5.Найти вероятность Р{-1 X 4}.
Непрерывные случайные величины.
Плотность распределения непрерывной случайной величины Х имеет вид:
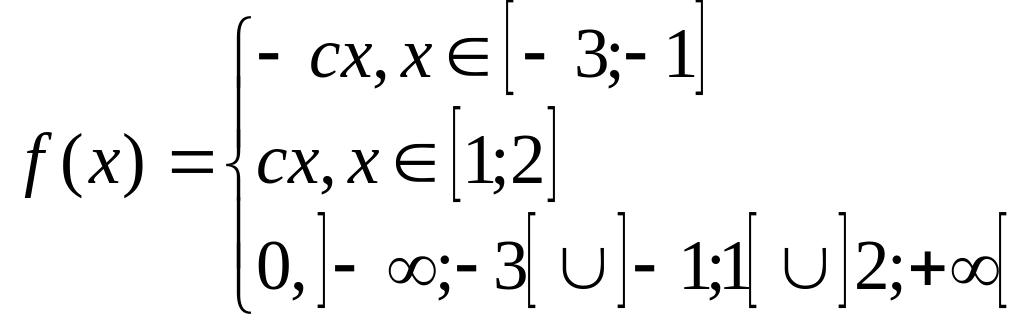
1.Найти константу с.
2.Найти математическое ожидание случайной величины Х.
3.Найти дисперсию случайной величины Х.
4.Построить графики плотности распределения и функции распределения случайной величины Х.
5. Найти P{X>0}, P{-2<X<1,5}.
Многомерные случайные величины.
Найти функцию распределения случайной величины Z=2X+Y, где X-дискретная случайная величина, принимающая два значения: 1 с вероятностью 0,7 и -1 c вероятностью 0,3, а Y имеет нормальное распределение с математическим ожиданием 0 и дисперсией 1; X и Y- независимы. Вычислить вероятность Р(Z<0).
Указание: воспользоваться формулой полной вероятности.
Непрерывная двумерная случайная величина (X,Y) равномерно распределена внутри прямоугольного треугольника с вершинами (-2;-1), (4;-1), (-2;1). Найти двумерную плотность совместного распределения и плотности распределения случайных величин X и Y. Вычислить коэффициент корреляции.
Предельные теоремы теории вероятностей.
Учебник издан тиражом 100000 экземпляров. Вероятность того, что учебник сброшюрован неправильно, равна 0,0001. Найти вероятность того, что тираж содержит ровно 5 бракованных книг.
Всхожесть семян данного растения равна 0,9.Найти вероятность того, что из 900 посаженных семян число проросших заключено между 790 и 830.
Устройство состоит из 10 независимо работающих элементов. Вероятность отказа каждого элемента за время Т равна 0,05. С помощью неравенства Чебышева оценить вероятность того, что абсолютная величина разности между числом отказавших элементов и средним числом отказов за время Т не меньше двух.
Математическая статистика.
По данному распределению выборки построить эмпирическую функцию распределения, гистограмму и полигон:
xi |
1 |
2 |
3 |
4 |
5 |
6 |
ni |
15 |
25 |
10 |
20 |
10 |
20 |
Найти точечную оценку параметра p биномиального распределения (схема Бернулли) по выборке (0,0,1,0,0,1,1,0,0,0,1,0), где Х
 принимает
значения: 1 с вероятностью р и 0 с
вероятностью 1-р: а) методом моментов и
б) методом максимального правдоподобия.
принимает
значения: 1 с вероятностью р и 0 с
вероятностью 1-р: а) методом моментов и
б) методом максимального правдоподобия.Найти доверительный интервал надежности 1-α=0,95 для неизвестного математического ожидания при неизвестной дисперсии по выборке Х
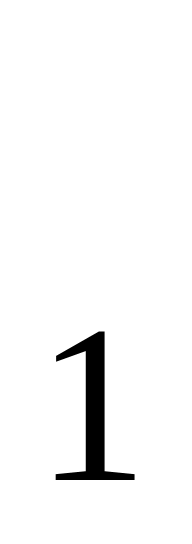 =0,464,
Х
=0,464,
Х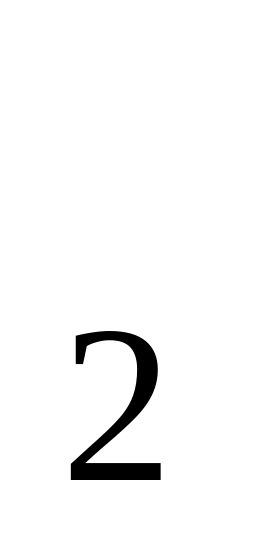 =0,137,
Х
=0,137,
Х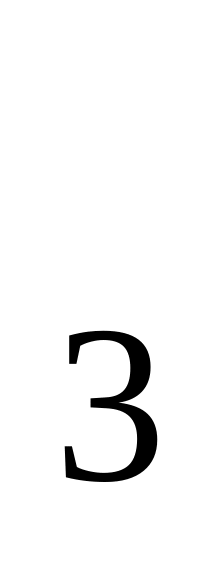 =2,455,
Х
=2,455,
Х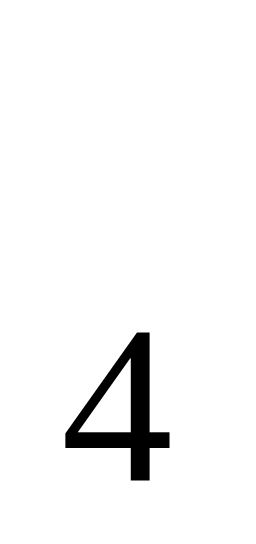 =-0,323.
Распределение нормальное. Какова
точность этого интервала? Как изменится
точность, если дисперсия известна и
равна 1,5?
=-0,323.
Распределение нормальное. Какова
точность этого интервала? Как изменится
точность, если дисперсия известна и
равна 1,5?Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза об экспоненциальном распределении генеральной совокупности с результатами наблюдений, представленными в таблице:
X |
0,1 |
0,3 |
0,5 |
0,7 |
0,9 |
1,3 |
1,5 |
1,7 |
1,9 |
2,4 |
2,9 |
3,8 |
n |
22 |
12 |
10 |
11 |
12 |
10 |
2 |
1 |
7 |
5 |
3 |
5 |
Вариант 2.
Операции над событиями.
Событие А – хотя бы одно из имеющихся изделий - бракованное , событие В – бракованных изделий не менее двух. Что означают события: АВ,
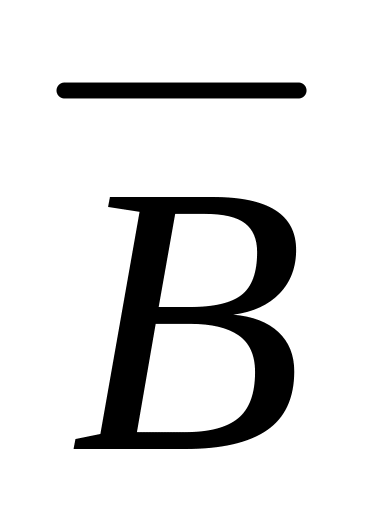 ,
,
 ,
А+В?
,
А+В?
Рабочий изготовил 5 деталей. Пусть событие Аi, i=1,…,5, заключается в том, что i–ая изготовленная им деталь имеет дефект. Записать событие, состоящее в том, что только третья деталь имеет дефект.
Классическое определение вероятности.
На полке стоят 6 книг в красном переплете и 4 книги в зеленом переплете. Наугад взято 7 книг. Найти вероятность того, что среди взятых книг 4 в красном переплете и 3 в зеленом.
Игральная кость бросается 2 раза. Найти вероятность того, что сумма очков заключена в интервале от 5 до 7 очков, включая эти значения.
Формула сложения и умножения вероятностей.
Формула полной вероятности.
Схема Бернулли.
Прибор проверяется контролером по двум независимым параметрам. Вероятность того, что прибор будет забракован по первому параметру, равно 0,1, а по второму – 0,15. Определить вероятность того, что прибор будет забракован хотя бы по одному параметру.
В вузе обучаются 70% юношей и 30% девушек. Среди юношей курят 20%, среди девушек – 5%. Найти вероятность того, что наудачу выбранный студент не курит.
Вероятность изготовления детали отличного качества равна 0,9. Какова вероятность того, что среди 10 деталей изготовленных деталей не менее 9 отличного качества.
