Виконання арифметичних операцій у пристроях із „плавучою” комою

Операція додавання у пристроях із „плавучою” комою відбувається у чотири етапи:

1. Порівнюються порядки доданків: менший порядок збільшується до більшого. При цьому відповідним чином корегується мантиса числа, яке перетворюється.

2. Виконується перетворення мантис у додаткові коди.

3. Виконується додавання мантис за правилами, розглянутими вище для чисел із фіксованої комою.

4. До суми приписується порядок доданків і, в разі необхідності, виконується нормалізація результату.

Операція множення чисел, поданих у формі з „плавучою” комою також виконується у чотири етапи:

1. Визначається знак добутку.

2. Перемножуються мантиси співмножників за правилами для чисел із фіксованою комою.

3. Обчислюється порядок добутку алгебраїчним додаванням порядків співмножників за правилами додавання цілих чисел із знаком.

4. Виконується нормалізація отриманого результату у випадку її необхідності.

Ділення чисел у пристроях із „плавучою” комою виконується так само, як і множення.

Висновки:

Операція віднімання в обчислювальних пристроях завжди заміняється операцією додавання з числом протилежного знака (доповненням модуля від’ємника).

Операції множення і ділення в обчислювальних пристроях виконуються у вигляді послідовності операцій додавання і зсування.

Таким чином, виконання усіх арифметичних операцій у ЕОМ так чи інакше зводиться до виконання послідовності дій, серед яких основною є додавання чисел, допоміжними – зсування, інверсія та ін. Тому всі ЦА, що виконують арифметичні операції, містять у своєму складі один або декілька суматорів.

5.2. Суматори

Суматором називається ЦА, що здійснює операції арифметичного додавання кодів двох чисел.

Суматори широко застосовуються у цифровій техніці. Наприклад, головна частина МП – АЛП, основою якого є багаторозрядний суматор. Суматори по модулю два (схеми згортки) використовуються як елементи ЛЗЗ у рекурентних регістрах та у складі лічильників, що працюють у коді Грея, в різноманітних перетворювачах кодів. У радіозв’язку цифрові пристрої формування сітки частот і різні пристрої цифрової обробки сигналів, зокрема цифрові фільтри, також містять пристрої додавання різних типів.

За ознакою реалізованої мікрооперації суматори поділяють на суматор за модулем два; напівсуматор та повний суматор.

За кількістю розрядів оброблюваних двійкових чисел суматори бувають однорозрядні і багаторозрядні.

За способом подання вхідних і вихідних кодових слів суматори можуть бути паралельні і послідовні.

За способом функціонування, суматори можуть бути як комбінаційними, так і послідовнісними (накопичувальними).

За ознакою використовуваної системи числення суматори діляться на двійкові і десяткові.

Комбінаційні однорозрядні суматори

Я

Таблиця 5.1

кщо подати правила додавання двійкових чисел, що були розглянуті раніше, у табличному вигляді, отримуємо таблицю функціонування двійкового однорозрядного суматора (табл. 5.1), у якій: A_i, B_i – однорозрядні доданки, S_i – молодший розряд суми, P_i – перенос до i‑го розряду із попереднього, P_i+1 – перенос до наступного старшого розряду із i‑го (старший розряд суми).

Pi	Ai	Bi	Si	Pi+1
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

З аналізу цієї таблиці видно, що її верхня половина без урахування стовпчиків P_i і P_i+1 (виділений фрагмент) є таблицею істинності логічного елемента „виключальне АБО” (суматора за модулем два), логічна функція якого має вигляд:

P i+1		Pi
	Ai
+	Bi
	Si

З аналізу значень стовпчика P_i+1 тієї ж верхньої половини таблиці (для P_i = 0) очевидно, що для реалізації операції додавання двох однорозрядних двійкових чисел з урахуванням переносу одиниці до старшого розряду (P_i+1 = 1 тільки при A_i = B_i = 1, таким чином P_i+1 = A_iB_i), суматор по модулю два треба доповнити елементом ТА, як показано на рисунку 5.1а. Такий функціональний елемент отримав назву однорозрядного напівсуматора або однорозрядного суматора на два входи (ОС-2). УГП напівсуматора показано на рисунку 5.1б.

Очевидним недоліком однорозрядного напівсуматора є те, що він при виконанні операції додавання не враховує переносу із попереднього розряду P_i. Цей недолік усунено у схемі повного однорозрядного суматора або однорозрядного суматора на три входи - (ОС‑3).

а) б)

Рис. 5.1. Двійковий однорозрядний напівсуматор

На підставі таблиці 5.1 запишемо логічні функції виходів S_i і P_i+1:

;

.

Використовуючи різні варіанти перетворення цих функцій, можна реалізувати велику кількість структур однорозрядних двійкових суматорів. Як приклад розглянемо побудову схеми суматора з використанням суматорів по модулю два і елементів ТА-НІ.

Застосовуючи розподільний закон і правило де Моргана, отримаємо:

Таким чином, для формування молодшого розряду суми S_i, у схемі ОС‑3 необхідно мати два суматори по модулю два.

Аналізуючи стовпчики A_i, B_i, P_i, P_i+1 таблиці 5.1, можна помітити, що вихідний сигнал схеми формування переносу до старшого розряду (старшого розряду суми) P_i+1 співпадає з більшістю вхідних сигналів A_i, B_i, P_i (якщо на входах одиниць більше, ніж нулів, то вихідний сигнал дорівнює 1 і навпаки). Такий комбінаційний вузол називають мажоритарним елементом.

Мінімізуємо логічну функцію для P_i+1 за допомогою карти Карно (рис. 5.2).

	1	1	1	0
	0	1	0	0

Рис. 5.2. Карта Карно для мажоритарного елемента з трьома входами

Отримаємо ЛФ мажоритарного елемента з трьома входами у вигляді мінімальної ДНФ:

.

Подамо отриману функцію у базисі ТА-НІ:

.

Схема однорозрядного комбінаційного суматора, побудованого на основі отриманих виразів, подана на рисунку 5.3.

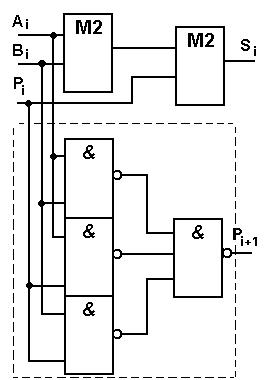
Рис. 5.3. Однорозрядний комбінаційний суматор

Інший варіант побудови однорозрядного комбінаційного суматора можна отримати, якщо, використовуючи розподільний закон і операцію склеювання, подати вираз для P_i+1 у вигляді:

.

Якщо взяти до уваги, що

, а ,

де S_iОС-2 і P_i+1ОС-2 – логічні функції суми і переносу на виході однорозрядного напівсуматора, остаточно отримаємо:

.

Відповідно, схема однорозрядного суматора на напівсуматорах має вигляд, показаний на рисунку 5.4а. УГП однорозрядного суматора показано на рисунку 5.4б.

а) б)

Рис. 5.4. Однорозрядний комбінаційний суматор та його УГП

В УГП напівсуматора і суматора дозволяється використовувати замість сполучень літер HS і SM символ .

Накопичувальний однорозрядний суматор

Розглянутий раніше Т ‑ тригер має цікаву властивість: відповідно до свого попереднього стану Q^t та вхідного сигналу Т він виконує операцію додавання за модулем 2, що пояснюється таблицею 5.2. Відповідно, цю властивість можна використати для побудови накопичувального (послідовнісного) двійкового суматора.

Очевидно, що для формування суми S_i за три такти (доданки повинні надходити на вхід тригера по черзі, по одному у кожному такті синхронізації) можна використати схему, що зображена на р исунку 5.5.

Qt	T	Qt+1
0	0	0
0	1	1
1	0	1
1	1	0

Таблиця 5.2

Рис. 5.5. Схема формування суми на основі Т-тригера

Отримати перенесення Р_і+1 можна за допомогою розглянутого раніше мажоритарного елемента на три входи, але ж наявність інверсного виходу тригера, де формується , дозволяє додатково спростити схему суматора.

Для синтезу схеми формування перенесення із таблиці 5.2, вважаючи Р_і, А_і, В_і, S_i аргументами функції Р_і+1, запишемо:

.

Враховуючи, що

(тому, що ), отримуємо:

Використовуючи розподільний закон та правила додатковості і повторення остаточно маємо:

Логічна схема накопичувального суматора, що реалізовує отримані вирази, зображена на рисунку 5.6.

Рис. 5.6. Схема накопичувального суматора

Багаторозрядні комбінаційні суматори

Принцип додавання багаторозрядних двійкових чисел полягає у тому, що у кожному з розрядів виконуються однотипні дії: визначається цифра суми шляхом додавання по модулю два цифр доданків і переносу з попереднього розряду та формується перенос до наступного розряду. Ці дії реалізовуються двійковим однорозрядним суматором. Така однотипність дій при додаванні окремих розрядів багаторозрядних чисел дозволяє реалізувати багаторозрядні суматори як у послідовному вигляді – за рахунок послідовного виконання додавання розрядів за допомогою одного однорозрядного суматора, так і у паралельному – за допомогою схеми, що вміщує кілька однотипних фрагментів (відповідно до кількості розрядів доданків), кожен з яких містить свій однорозрядний суматор.

Паралельний багаторозрядний суматор складається з такої кількості однорозрядних суматорів, яка дорівнює кількості розрядів чисел, які додаються.

Усі розряди доданків повинні одночасно надходити до пристрою додавання. Сигнал переносу передається від розряду до розряду послідовно, утворюючи на виході значення старшого розряду суми. Схема паралельного дворозрядного комбінаційного суматора з послідовним переносом показана на рисунку 5.7.

Рис. 5.7. Дворозрядний комбінаційний паралельний суматор з послідовним переносом

Недоліком суматора з послідовним переносом є те, що отримання результату у старшому розряді суматора можливе тільки після завершення розповсюдження переносу по усіх розрядах, що знижує швидкодію пристрою. Тому інколи у схемах паралельних суматорів організовують прискорений перенос. Для цього у кожному однорозрядному двійковому суматорі додатково формується сигнал розповсюдження переносу. Ідея прискорення переносу полягає у тому, що при А_i = B_i = 1 у i-му розряді буде мати місце перенос до наступного розряду, незалежно від наявності переносу із попереднього розряду (і навпаки – при А_i = B_i = 0 у i-му розряді не буде переносу до наступного розряду, незалежно від наявності переносу із попереднього розряду). Таким чином у деяких випадках можна формувати сигнал переносу для обчислення старших розрядів, не чекаючи закінчення формування переносу із молодших розрядів. Перевірка умов, за якими можливе формування „прискореного” переносу, може бути виконана за допомогою додаткових елементів ТА і АБО.

Послідовний багаторозрядний суматор складається з одного однорозрядного суматора та елемента затримки – D-тригера, що здійснює затримку сигналу переносу на один робочий такт – до надходження до входів суматора наступних (старших) розрядів доданків. Схема такого суматора показана на рисунку 5.8.

Регістри зсуву в схемі призначені для передавання до входів суматора розрядів доданків у послідовному коді, починаючи з молодшого розряду, та приймання обчислених суматором розрядів суми.

Рис. 5.8. Послідовний багаторозрядний суматор

З першим тактовим імпульсом на входи суматора надходять із регістрів 1 і 2 молодші розряди доданків А_i і B_i, а до входу переносу подається із D-тригера логічний 0. Додаючи подані на входи цифри, однорозрядний суматор формує молодший розряд суми, який надходить до регістра зсуву 3 і перенос, який надходить до D-тригера. Другий тактовий імпульс реалізовує в усіх регістрах зсув їхнього вмісту на один розряд праворуч; при цьому на входи однорозрядного суматора надходять цифри наступних розрядів доданків, і значення переносу із D-тригера. У подальшому робочий цикл повторюється до тих пір, поки не будуть підсумовані усі розряди доданків.

Явна перевага суматора послідовної дії полягає у малих апаратних витратах на його побудову. Але такий суматор, у порівнянні з більш складним паралельним, має меншу швидкодію.

Пристрій додавання та віднімання чисел із знаком

Комбінаційний суматор у сукупності з деякими допоміжними елементами може бути використаний не тільки для додавання, але також для віднімання двійкових чисел із знаком. Зокрема для виконання віднімання у додаткових кодах за допомогою суматора до від’ємника необхідно застосувати операцію доповнення, що відповідає зміні знака операнда на протилежний. Для цього в схемі пристрою додавання і віднімання необхідно мати пристрій, що виконує при необхідності доповнення від’ємника (інверсію всіх розрядів вихідного коду, включаючи знаковий, та додавання одиниці до молодшого розряду).

Схема чотирирозрядного пристрою додавання і віднімання двійкових чисел у додаткових кодах подана на рисунку 5.9.

Тут:

– додатковий код операнда Х;

– додатковий код операнда Y;

– додатковий код результату.

Суматор SM виконує операцію:

.

Якщо сигнал керування Z = P1 = 0, то коди операндів подаються на входи суматора без зміни, і відбувається їх додавання:

.

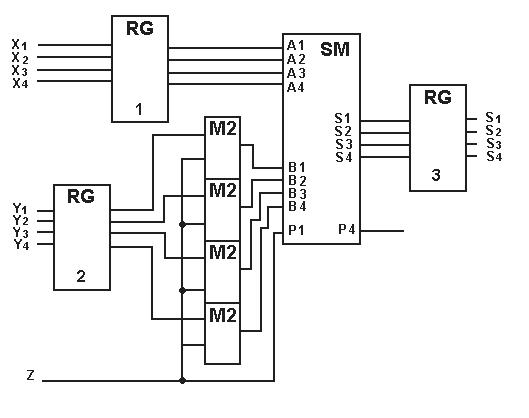
Рис. 5.9. Схема пристрою додавання і віднімання двійкових чисел

Якщо сигнал керування Z = P1 = 1, то відбувається інвертування значень усіх розрядів коду і по каналу переносу P1 у молодший розряд додається одиниця:

.

Враховуючи те, що , остаточно отримуємо:

,

що рівнозначно виконанню операції віднімання.

Розглянемо виконання операції віднімання чисел із знаком на прикладі 5-(-3) = -2:

_X= - 0,101

Y= - 0,011

S= - 0,010

На вхід пристрою операнди надходять у додаткових кодах: ; . Після інверсії коду ( ) і додавання одиниці до молодшого розряду одержимо .

Додатковий код різниці знайдемо як суму і :

1.011

+0.011

1.110

Отриманий код дійсно є додатковим кодом результату -0.010₂.