3. Решение систем нелинейных уравнений

Положим, имеется система двух нелинейных уравнений:

которые надо решить, т.е. найти точки их пересечения.

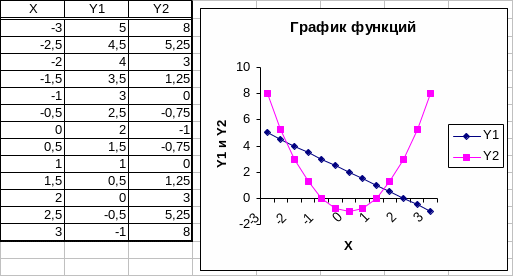
Как видно на графике, такая система имеет две точки пересечения. Для решения системы надо построить таблицу, где в клетках В2 и В3 ввести обе функции, которые в качестве аргумента Х ссылаются на ячейку А2. Кроме того, для контроля вычислений в С2 вводится целевая функция, которая вычисляет среднее отклонение значений функций друг от друга. Очевидно, если эти функции пересекаются (т.е. имеются решения), С2=0. Для розыска корня в окно Поиск решения вводятся необходимые параметры процесса. Результат вычислений существенно зависит от начального значения, заданного в качестве решения. Ниже приведен исходный и конечный вид таблицы, если задать его равным +10.

Начальное значение	Формулы	Целевая функция		Начальное значение	Формулы	Целевая функция
10	99	53,5		1,302776	0,697224	2,07E-08
	-8				0,697224

Если начальное значение задать равным –10, то исходный и конечный вид таблицы будет иметь вид:

Начальное значение	Формулы	Целевая функция		Начальное значение	Формулы	Целевая функция
-10	99	43,5		-2,30278	4,302776	2,44E-08
	12				4,302776

Таким образом, в обоих случаях найдены два разных решения.

4. Решение систем линейных уравнений

Нужно найти решение (корни) следующей системы линейных алгебраических уравнений:

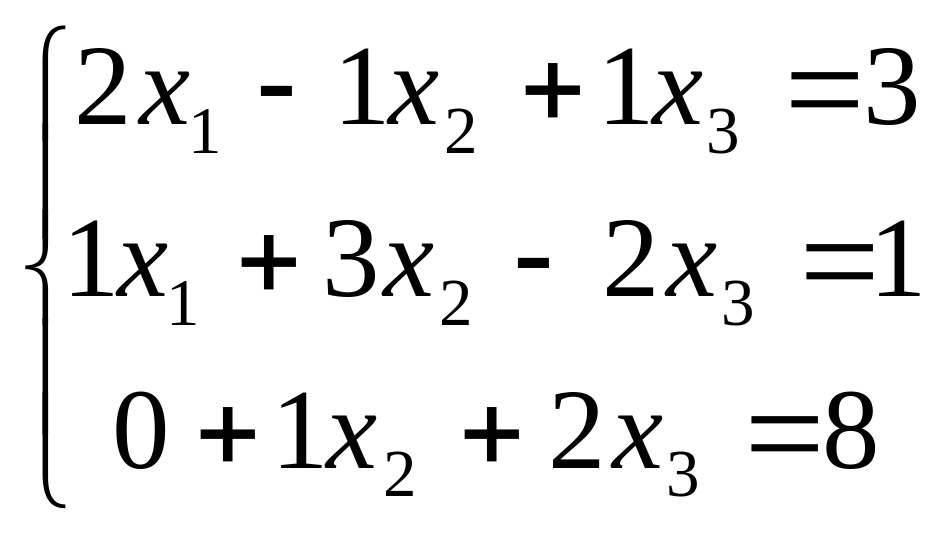
Внести коэффициенты системы в таблицу в столбцы А, В и С. Свободные члены внести в столбец Е. В столбец D внести формулы вычисления свободных членов (D2=СУММПРОИЗВ($A$6:$C$6;A2:C2)). Задача состоит в том, чтобы добиться совпадения значений вычисленных и фактических значений столбцов D и Е. В качестве изменяемых значений используем ячейки А6, В6,С6. Первоначально они остаются пустыми, т.е. равными нулю. В окне Поиск решения вводятся значения только параметров: Изменяемые ячейки ($A$6:$C$6;A2:C2) и Ограничения ($D$2:$D$4=$E$2:$E$4).

X1	X2	X3	Левая часть	Свободные члены
2	-1	1	3	3
1	3	-2	1	1
0	1	2	8	8
Корни:
1	2	3

Получены три корня: Х1=1, Х2=2, Х3+3.