Лекція 2 Перехідні процеси в лінійному ланцюзі з ємністю

Розглянемо перехідні процеси в ланцюзі, що складається з елементів ємності й активного опору, при вмиканні його під постійну й синусоїдальну напруги, а також при замиканні накоротко.

Включення ланцюга з елементами R і С під постійну напругу. При вмиканні ланцюга з R і C (рис. 2.1, а) під постійну напругу U, відповідно до другого закону Кірхгофа, можна записати:

(2.1)

Тому що сила струму в ланцюзі являє собою швидкість зміни заряду , то рівняння (2.1) можна переписати у виді:

Розділюючи змінні, отримаємо:

де – електромагнітна постійна часу ланцюга.

Інтегруючи останнє диференціальне рівняння і потім зробивши потенціювання результату, знайдемо:

(2.2)

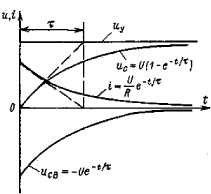
Рис. 2.1. Ввімкнення ланцюга з елементами R, С під постійну напругу:

a — схема ланцюга; б — криві напруги й струму

Постійна інтегрування А знаходиться з початкових умов: при t=0 та u_C(0)=0 і, отже, А =U. Підставляючи це у вираз (1.17) і, вирішуючи його щодо напруги и_с, одержимо:

(2.3)

Сила струму в ланцюзі визначиться рівнянням:

(2.4)

На рис. 2.1, б побудовані криві u_C=f(t) та i =f(t). Напруга u_C плавно зростає до сталого значення, а сила струму i у міру заряду конденсатора поступово зменшується, асимптотична наближаючись до нуля.

Теоретично заряд конденсатора закінчується при . Практично ж заряд конденсатора вважається закінченим, коли , що має місце при .

Замикання ланцюга з елементами R і С накоротко. Якщо ланцюг з елементами R, C (рис. 2.2, а) увімкнути до джерела живлення, а потім замкнути накоротко, то елемент ємності буде розряджатися. У цьому випадку рівняння електричної рівноваги запишеться у наступному виді:

Розділяючи змінні, отримаємо:

Інтегруючи це рівняння і потім здійснюючи потенціювання, відповідно знайдемо:

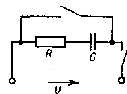
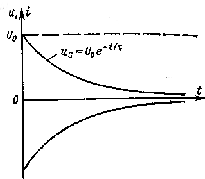
Рис. 2.2. Коротке замикання ланцюга з елементами R i C:

а — схема ланцюга; б — криві напруги й струму

Постійну інтегрування А визначають із початкових умов: при t=0, u_с(0) = U₀ і, отже, напруга при розряді конденсатора буде дорівнювати:

(2.5)

Сила струму в ланцюзі при розряді конденсатора знаходиться за виразом:

На рис. 2.2, б зображені криві . Вважається, що при t=4,6·τ , коли u_с = 0,01·U₀ та і=0,01·І, розряд конденсатора практично закінчується.

Енергетичні процеси у ланцюзі з елементами R і С. З енергетичної точки зору перехідні процеси при заряді конденсатора відбуваються за рахунок перетворення енергії системи. Дійсно, при вмиканні ланцюга струм, проходячи по елементові опору R, нагріває його, а напруга на елементі ємності C створює електричне поле, у якому накопичується енергія. Справді, звертаючись до рівняння (1.16) і, множачи обидві його частини на idt, одержимо:

(2.6)

Де – енергія, що витрачається джерелом живлення; – енергія, перетворена в теплоту; – енергія, що накопичується в електричному полі. Таким чином, одна половина енергії, що витрачається джерелом, перетвориться у теплоту, а інша накопичується у електричному полі конденсатора. Процес розряду конденсатора з енергетичної точки зору характеризується перетворенням енергії, накопиченої в електричному полі конденсатора, у теплоту.

Вмикання ланцюга з елементами R і C під синусоїдальну напругу. При вмиканні ланцюга з елементами R і C (рис. 2.3, а) під синусоїдальну напругу рівняння електричної рівноваги для миттєвих значень матиме вид:

(2.7)

а) б) в)

Рис. 2.3. Вмикання ланцюга з елементами R, C під синусоїдальну напругу:

а – схема ланцюга; б – криві напруги; в – криві струму

Напруга на конденсаторі буде являти собою суму сталої u_Cс і вільної u_Cв напруг. Ці складові відповідно дорівнюють:

де

Отже, перехідна напруга на конденсаторі буде дорівнювати:

Постійна інтегрування А визначається за початковими умовами: якщо при t=0 та u_с(0) =0, то

Таким чином, закон зміни напруги буде наступний:

(2.8)

Звідси випливає, що під час перехідного процесу на синусоїдальну сталу напругу накладається вільна напруга, абсолютна величина якої зменшується по показовому законі. На рис. 2.3, б приведені криві їхньої зміни.

Процес заряду закінчується при t=4,6·, коли и_с практично досягає сталого значення. Варто враховувати, що значення u_C залежить не тільки від амплітуди напруги на затисках ланцюга, але й від моменту вмикання. Найбільше сприятливо процес протікає, коли у момент вмикання u_Cу = 0. У цьому випадку, як видно з рівняння (2.8), перехідний процес є відсутній, і у ланцюзі відразу настає сталий режим роботи.

Найбільшого можливого значення и_с досягає у тому випадку, якщо в момент вмикання u_Cc (0) = U_Cm, що може бути за умови ψ=φ або ψ-φ=π. У цьому випадку, якщо активний опір дорівнює нулю, через напівперіод після вмикання ланцюга напруга на конденсаторі може досягти значення:

Сила струму в ланцюзі при перехідному процесі визначається виразом:

Звідси випливає, що на початку процесу струм має несинусоїдний характер, а через час t=4,6τ практично приймає синусоїдальну форму. На рис. 2.3, в зображені криві сили струму при ψ=φ. У момент t=0 стала складова струму проходить через нуль, а вільна складова робить стрибок, який дорівнює , і потім спадає за експоненціальним законом. При малому значенні R початкові кидки сили токи можуть бути значними викликати в установці небажані динамічні зусилля.