Модель идеального смешения (мис)

Другой крайне идеализированной, но противоположной по смыслу моделью является МИС. Предполагается, что любая порция входящего в аппарат потока мгновенно равномерно перемешивается во всем объеме. Координаты и скорость отдельного элемента потока в каждый момент времени, а также время его пребывания в аппарате имеют чисто случайное значение. Концентрация меченых элементов потока одинакова во всех точках аппарата.

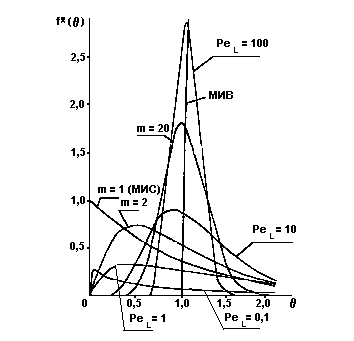
Рис.6 Вид функций распределения для различных моделей при определенных значениях параметров: m - числа ячеек (ячеечная модель) и

Ре_L - критерия Пекле для продольного перемещения (диффузионная модель).

Для получения математической модели МИС нет необходимости использовать исчерпывающее описание, представляющее собой локальную форму законов сохранения. Поскольку концентрация меченых элементов потока предполагается одинаковой во всех точках аппарата проще воспользоваться интегральной формой закона сохранения массы (то есть для всего аппарата) или точнее его аналогом - законом сохранения количества меченых элементов потока.

По аналогии с (21) можно записать

(84)

G_Nвх, G_Nвых - количество меченых элементов потока, входящих в аппарат и выходящих из него за единицу времени. Как и при рассмотрении МИВ, пометим элементы потока лишь в начальный момент времени. При любых t > 0 входа меченых элементов в аппарат не будет (G_Nвх=0,t>0). G_Nвых можно определить через объемный расход выходящего потока G_v и концентрацию в нем меченых элементов (она будет соответствовать их концентрации в самом аппарате). Так как концентрация c(x,t) одинакова во всех точках аппарата, то ее можно считать функцией одного аргумента c(x,t)=c(L,t)=c(t), обозначив для краткости c. (85)

С начальными условиями c(0) = c₀ решение получим в виде

; (86)

Наиболее близка к МИС структура мало вязкого потока, движущегося с небольшой расходной скоростью через аппарат с интенсивно работающей мешалкой.

Ячеечная модель (мя)

Более реалистичной моделью является МЯ, в соответствии с которой предполагается последовательное прохождение потоком ряда ячеек идеального смешения. Параметром модели является число таких ячеек m. Учитывая, что объем каждой ячейки равен отношению объема всего аппарата к числу ячеек, а концентрация меченых элементов потока на входе в ячейку соответствует их концентрации на выходе из предыдущей, можно получить для i-й ячейки

(87)

Решение системы m дифференциальных уравнений (87) дает выражение для концентрации меченых элементов в последней ячейке, то есть на выходе из аппарата c_m(t).

Нетрудно убедиться, что при m=1 МЯ переходит в МИС, а при m= в МИВ (рис.6). Наиболее приемлемое описание МЯ дает для каскада аппаратов с мешалками и других аппаратов ступенчатого типа.

Диффузионная модель (мд)

Другой моделью промежуточного типа является МД. Считается, что отклонение в движении элементов потока от идеального вытеснения осуществляется за счет их случайных блужданий, которые могут быть описаны по аналогии с молекулярным или турбулентным механизмами переноса. Это позволяет воспользоваться уравнением нестационарной конвективной диффузии для определения концентрации меченых элементов потока c(x,t), полагая конвективную скорость, равной для всех элементов, а перемешивание вне зависимости от причин его вызывающих учитывать с помощью коэффициента обратного (продольного) перемешивания D_L. Тогда получим (88)

где D_L может быть найдено из Pe_L=W_xL/D_L - критерий Пекле для продольного перемешивания (параметр модели). При Pe_L=0 МД переходит в МИС, а при Pe_L= в МИВ (рис.6).

Необходимо помнить, что D_L учитывает суммарное отклонение от идеального вытеснения за счет всех механизмов переноса (конвективного, турбулентного, молекулярного) и не может отождествляться с коэффициентом турбулентной или молекулярной диффузии. Обычно МД применяют для аппаратов, характеристики потоков в которых изменяются по длине непрерывно.

Нами рассмотрены наиболее простые модели структуры потоков в аппаратах. Существуют и более сложные, например, двухпараметрическая диффузионная модель учитывает перемешивание не только в продольном, но и в радиальном направлении коэффициентом D_r (двумерная постановка задачи c(x,r,t)). В сложных случаях применяют комбинированные модели, описывая различные характерные зоны аппарата разными математическими моделями. Однако, предоставляя возможность более точно воспроизвести структуру потока в реальном аппарате, сложные модели обладают и недостатком - трудностью определения большого числа параметров. Таким образом, мы подходим ко второму этапу математического моделирования.