Математическое моделирование структуры потоков

Наиболее корректной математической моделью структуры потоков в аппарате является исчерпывающее описание. Решение системы уравнений неразрывности и движения совместно с условиями однозначности позволило бы найти поле скоростей в аппарате. Однако получить такое решение для большинства случаев невозможно. Поэтому на практике идут по пути упрощения модели, используя для характеристики структуры потока функцию распределения времени пребывания элементов потока в аппарате. Рассмотрим последовательно этапы математического моделирования на примере полого цилиндрического проточного аппарата.

На рис.4. показаны экспериментально найденные профили скоростей W_х в некоторых сечениях. Поскольку движение считается осесимметричным в верхней половине аппарата распределение скоростей будет иметь аналогичный вид. Как видим, поле скорости даже такого простого аппарата имеет существенную неоднородность.

Можно выделить две наиболее упрощенные идеализированные модели, характеризующие предельные ситуации: идеальное вытеснение и идеальное смешение, а также более реалистичные модели промежуточного типа, к которым относятся ячеечная и диффузионная модели.

Рис.4. Поле скорости W_x и характерные зоны в горизонтальном цилиндрическом проточном аппарате: 1,7 - застойные зоны; 2,6 - зоны смешения; 3 - пограничный слой; 4,5,8 - ядро потока.

Модель идеального вытеснения (мив)

Согласно этой модели все элементы потока движутся по параллельным траекториям с одинаковыми скоростями (рис.5). Время пребывания в аппарате для всех элементов такого потока одинаково.

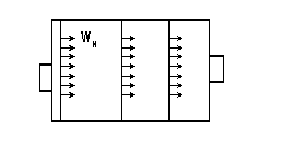
Рис.5 Поле скорости W_x для модели идеального вытеснения.

Следовательно, во-первых, допущение о равенстве и постоянстве скоростей всех элементов потока позволяет сократить размерность задачи до одномерной, совместив ось X с направлением вектора скорости, во-вторых, отпадает необходимость решения уравнений неразрывности и движения для определения скорости, так как она может считаться заданной, в-третьих, отсутствие перемешивания элементов потока позволяет считать равными нулю коэффициенты диффузии (D_ij, D_т =0). Тогда

(81)

или для одномерного случая (82)

где c=c(x,t) - концентрация меченых элементов потока в сечении аппарата с координатой x в момент времени t. Для нахождения решения необходимо дополнить уравнение (82) начальными и граничными условиями.

Для достижения нашей цели достаточно знать решение в сечении x=L, то есть на выходе из аппарата. Оно имеет вид

(83)

Полученные результаты имеют достаточно простой физический смысл. Поскольку все элементы потока движутся с одинаковой скоростью, то будут иметь одинаковое время пребывания в аппарате, совпадающее со средним. И если мы пометим элементы потока в узком слое на входе в аппарат, то выйдут они из аппарата все вместе через промежуток времени t = . Разумеется, на практике такая ситуация никогда не реализуется, так как для этого необходимо движение потока без трения на границах. Наиболее близка к МИВ структура турбулентного потока, движущегося по трубе при L/d>>1.