
Министерство образования Российской федерации
Южно-Уральский государственный университет
Кафедра математического анализа
Резников Е.А.
ВЫСШАЯ МАТЕМАТИКА
Сборник домашних контрольных заданий
для студентов-заочников
Челябинск
Издательство ЮУрГУ
2007
УДК 510(022)(076.5)
Резников Е.А. Высшая математика: Сборник домашних контрольных заданий для студентов-заочников. – Челябинск: Изд-во ЮУрГУ, 2007. – 19 с.
Сборник домашних контрольных работ состоит из четырех контрольных работ по следующим темам: «Элементы линейной алгебры, векторная алгебра и аналитическая геометрия», «Введение в анализ», «Дифференциальное исчисление функции одной переменной», «Интегральной исчисление функции одной переменной».
Задания составлены в соответствии с требованиями государственного общеобразовательного стандарта высшего профессионального образования.
Одобрено объединенным научно-методическим советом по математике и механике.
Рецензенты:
© Издательство ЮУрГУ, 2007.
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
В соответствии с учебным планом студенты-заочники выполняют контрольные работы по курсу высшей математики. Данный сборник контрольных заданий содержит контрольные работы, выполняемые на первом курсе. В первом семестре выполняются первая и вторая, во втором семестре - третья и четвертая контрольные работы.
Контрольная работа должна удовлетворять следующим требованиям:
Работу рекомендуется выполнять в ученической тетради в клеточку, авторучкой с синей или черной пастой. Цветную пасту можно употреблять для рисунков, графиков и т.п.
Нужно оставить свободное место за полями. Если в тетради нет черты, ограничивающей поле, ее следует провести.
Обязательно записать полностью условия всех решаемых задач – по тексту методического пособия.
Задачи (и их решения) следует располагать в том порядке, в каком они даны в методическом пособии.
Записи вести аккуратно, разборчивым почерком. Зачеркивания, помарки, обширные исправления не допускаются. Графики рисовать аккуратно, с указанием (и соблюдением) масштаба. Черновики не присылать!
Решения должны сопровождаться краткими, но вразумительными объяснениями, в необходимых случаях должны быть ссылки на учебник. Например, “составляем уравнение прямой, проходящей через две точки…”, ”в силу геометрического смысла векторного произведения…”, “По определению непрерывности функции в точке…” и т.п.
Объяснения должны относиться строго к тексту задачи и, соответственно, к теме разделу вузовского учебника. Формулы сокращенного умножения, решение квадратных уравнений и теорему Пифагора объяснять не нужно.
При работе над ошибками – читать замечания и указания проверяющего и, по возможности, выполнять их в работе, присылаемой на повторную проверку – вместе с предыдущей работой!
Перед отправкой работы необходимо проверить (по учебнику или словарю) правильность написания таких слов как “предел”, “эллипс”, “асимптота”, “дифференциал” и т.п. Грамматические ошибки в математических терминах приравниваются к ошибкам в ходе решения.
10) Берегите время! При несоблюдении требований 1-9 работа может быть возвращена без проверки для повторного выполнения.
На внешней обложке тетради следует указать фамилию и инициалы студента, полный учебный шифр и дату отправки работы в университет.
Студент выполняет тот вариант задачи контрольной работы, который совпадает с последней цифрой его учебного шифра. Цифра 0 соответствует варианту № 10.
Литература:
1.Письменный Д.Т. Конспект лекций по высшей математике. 1 часть.
2.Лунгу К.Н. и др. Сборник задач по высшей математике. Линейная алгебра. Аналитическая геометрия. Основы математического анализа.
3.Данко П.Е. и др. Высшая математика в упражнениях и задачах. Часть 1.
4.Пискунов Н.С. Дифференциальное и интегральное исчисления. Том 1.
КОНТРОЛЬНАЯ РАБОТА № 1
Линейная алгебра
ЗАДАЧА 1
Вычислить определитель.
1.1.
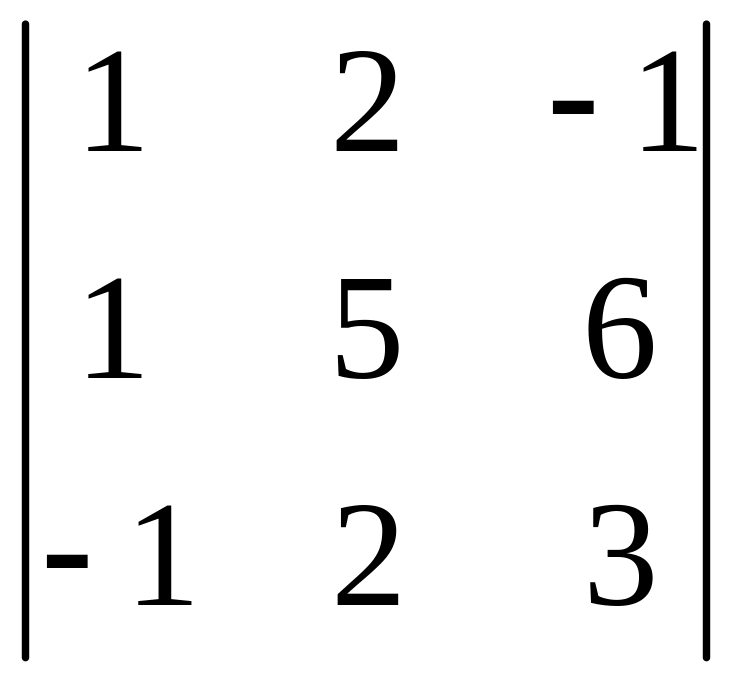 .
1.2.
.
1.2.
 .
1.3.
.
1.3.
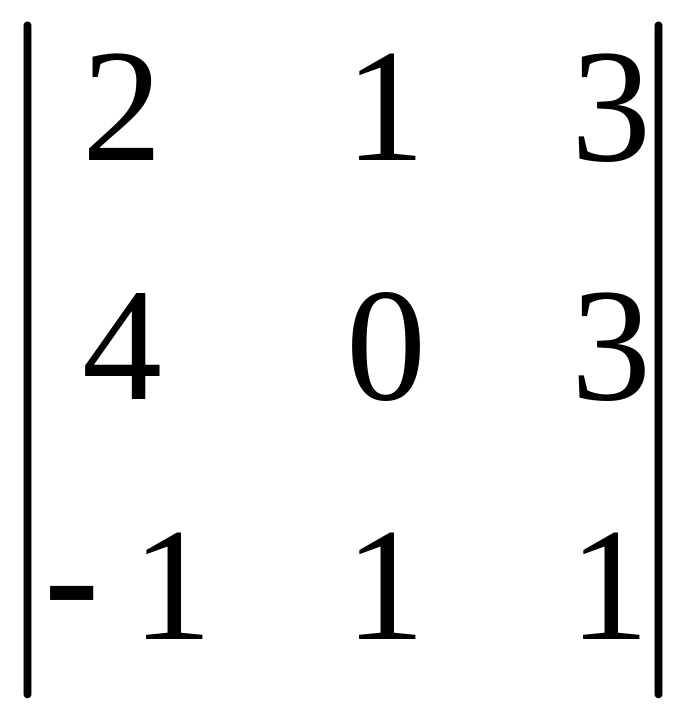 .
1.4.
.
1.4.
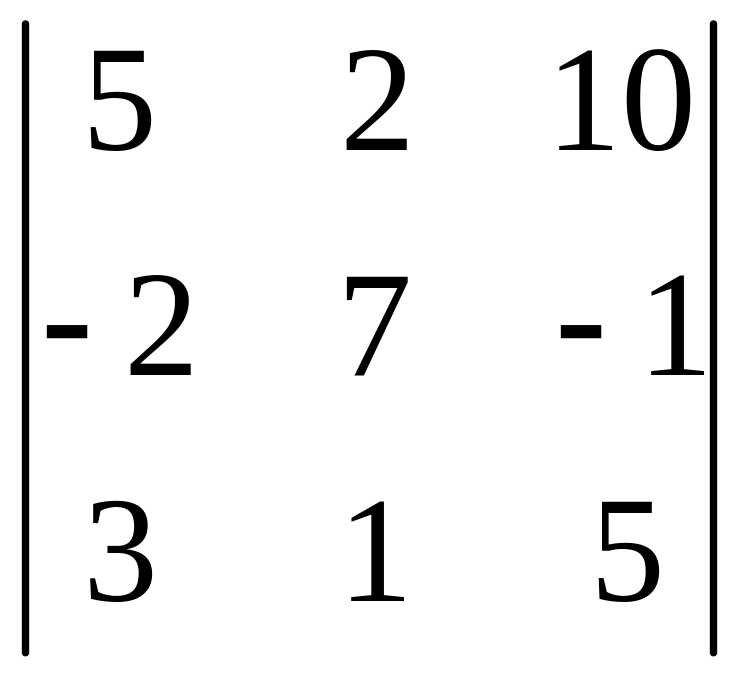 .
.
1.5.
 .
1.6.
.
1.6.
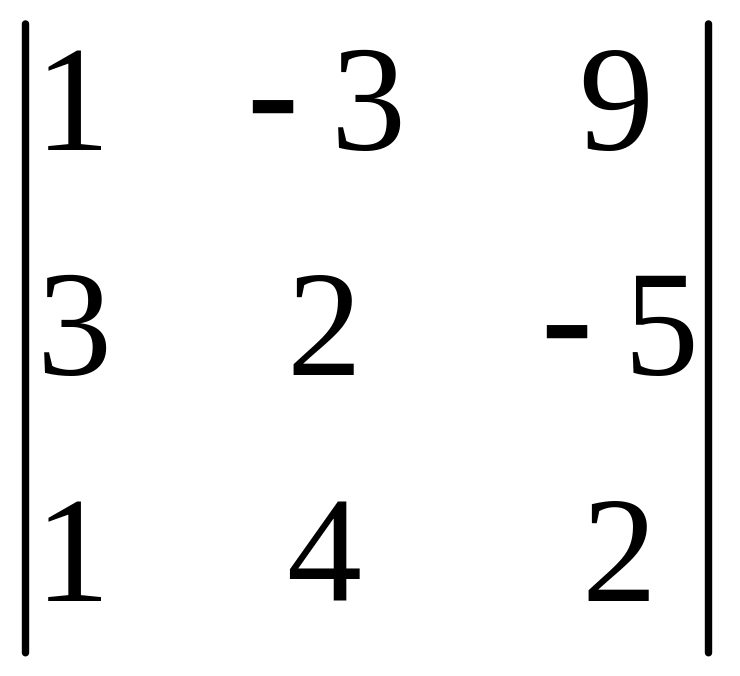 .
1.7.
.
1.7.
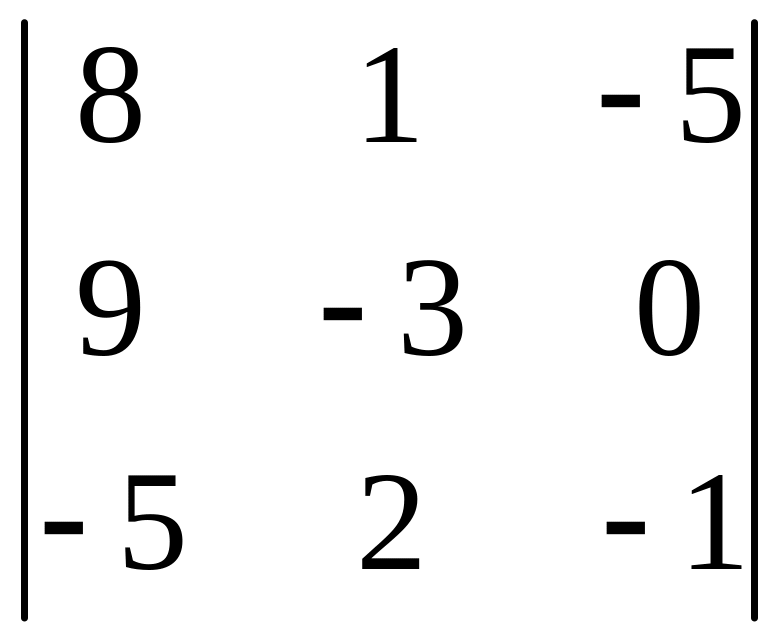 .
1.8.
.
1.8.
 .
1.9.
.
1.9.
 .
1.10.
.
1.10.
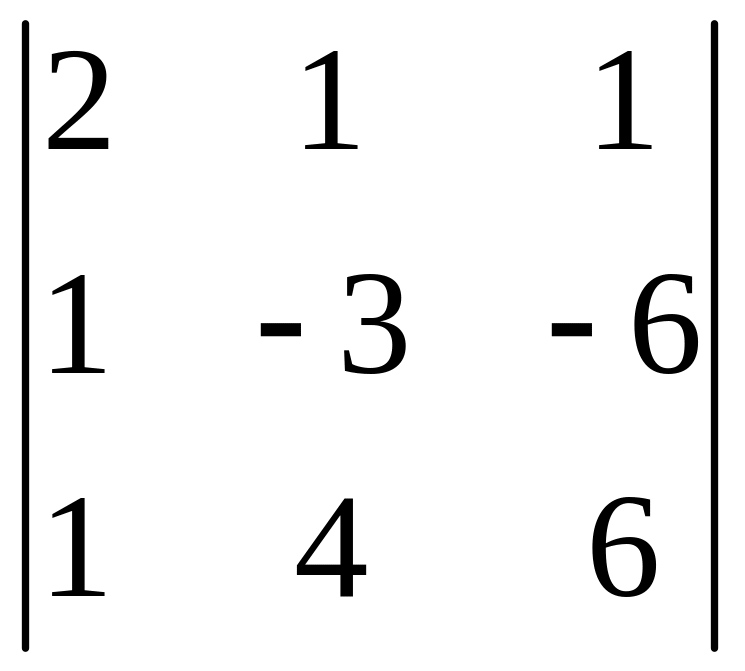 .
.
ЗАДАЧА 2
Найти матрицу Х из матричного уравнения (решать, используя обратную матрицу).
2.1.
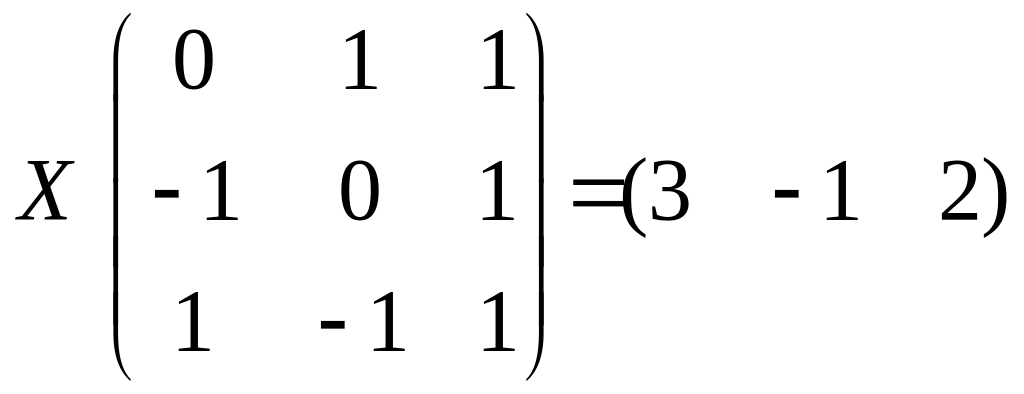 .
2.2.
.
2.2.
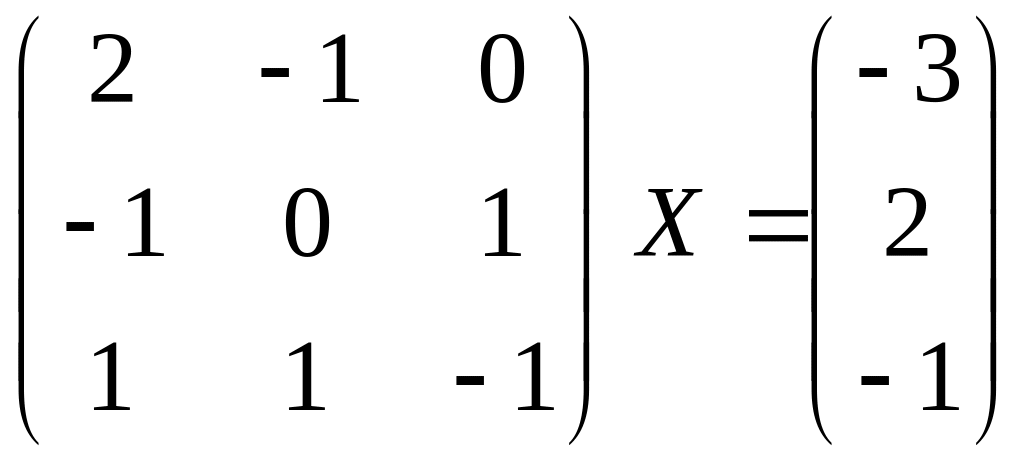 .
.
2.3.
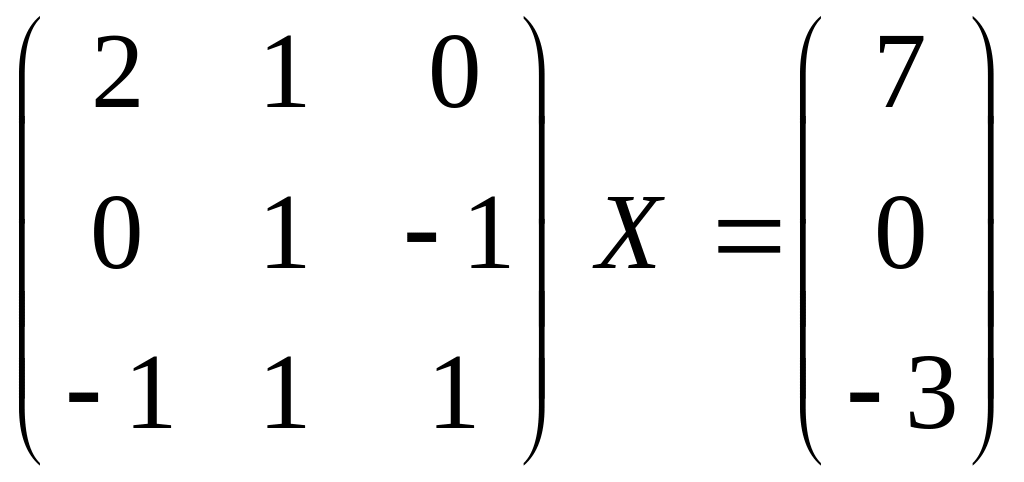 .
2.4.
.
2.4.
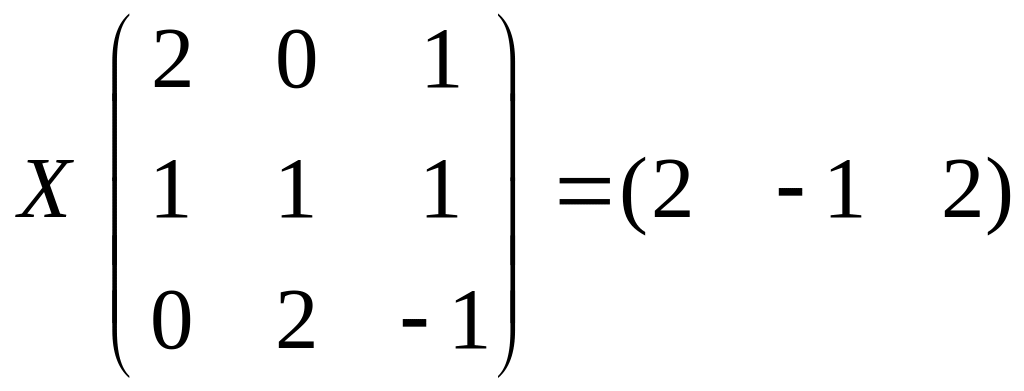 .
.
2.5.
 .
2.6.
.
2.6.
 .
.
2.7.
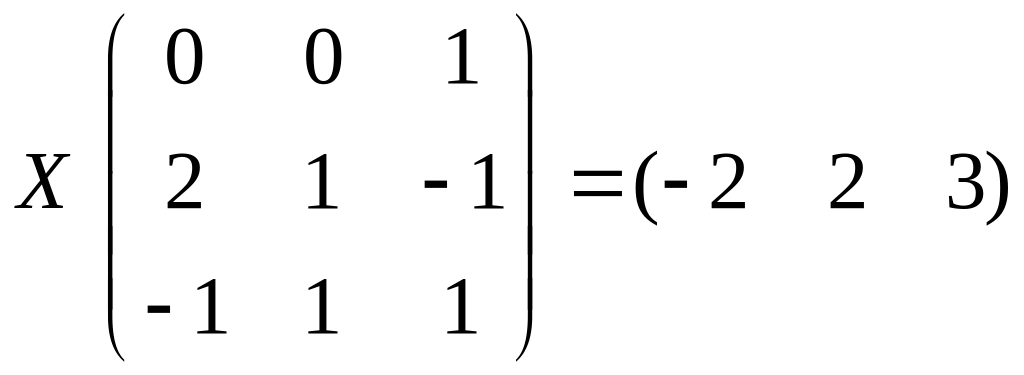 .
2.8.
.
2.8.
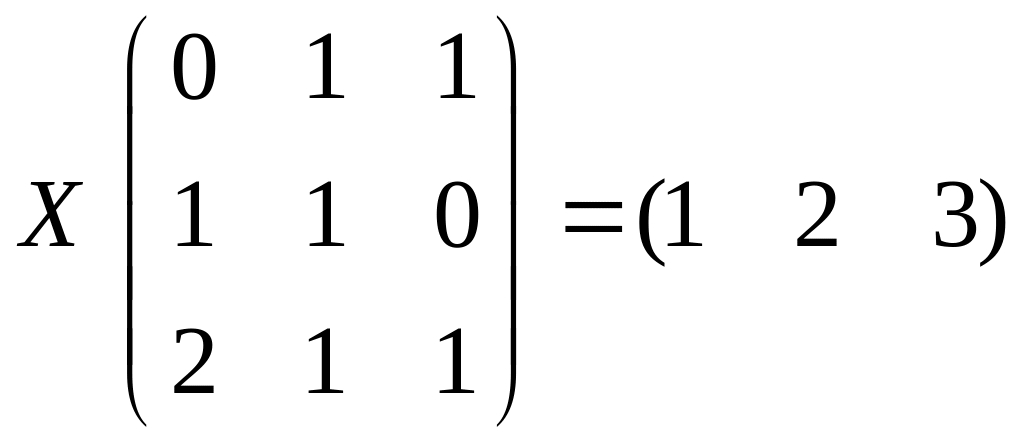 .
.
2.9.
 .
2.10.
.
2.10.
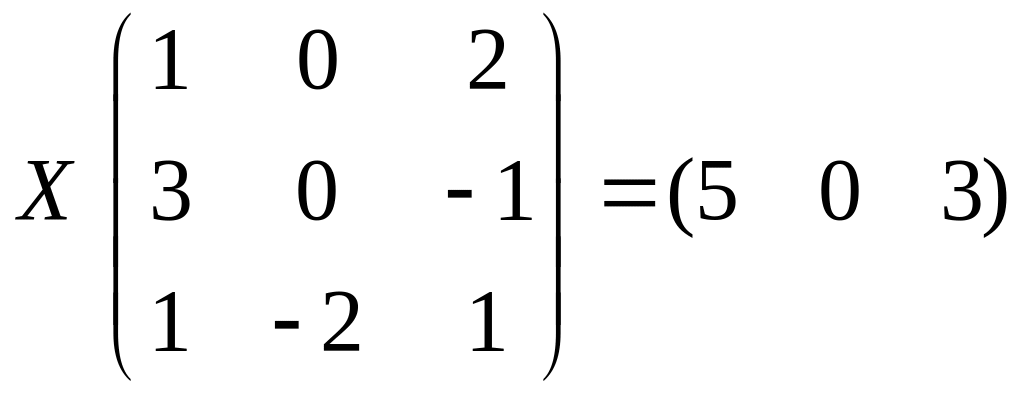 .
.
ЗАДАЧА 3
Решить систему уравнений методом Гаусса.
3.1.
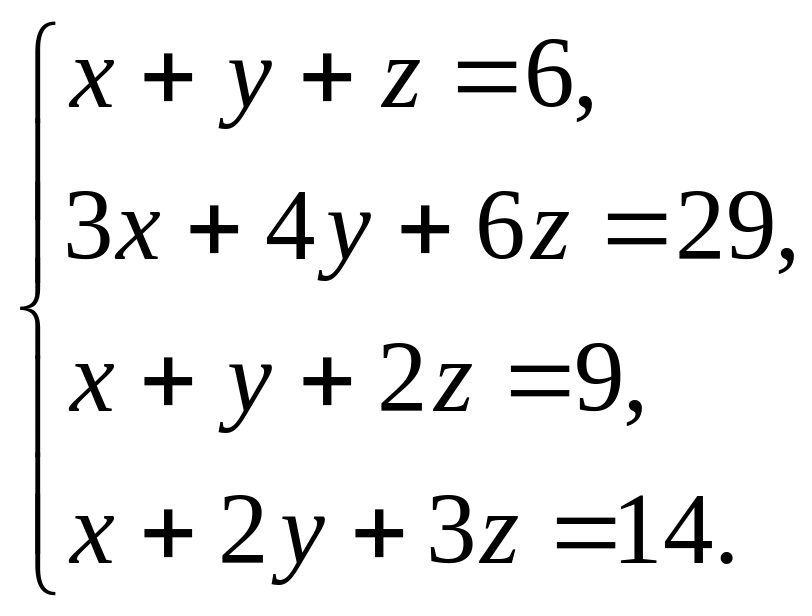 .
3.2.
.
3.2.
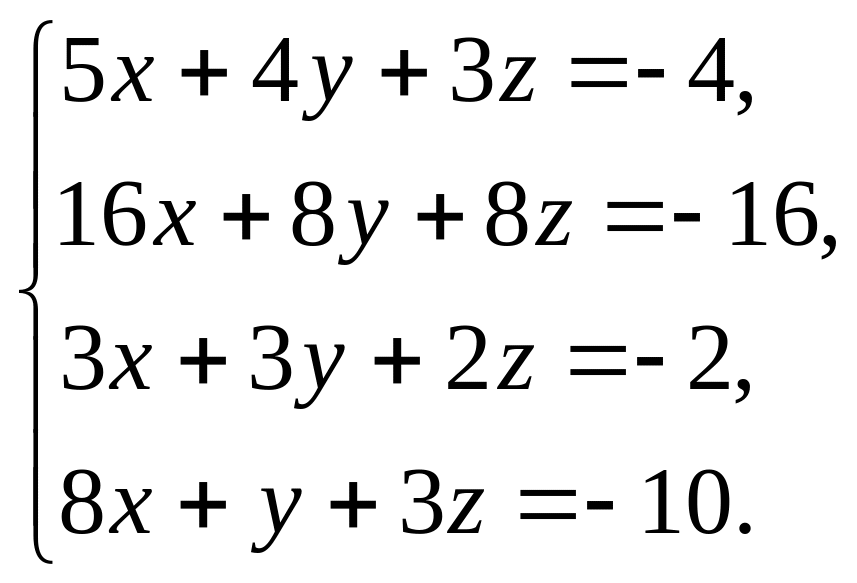 .
3.3.
.
3.3.
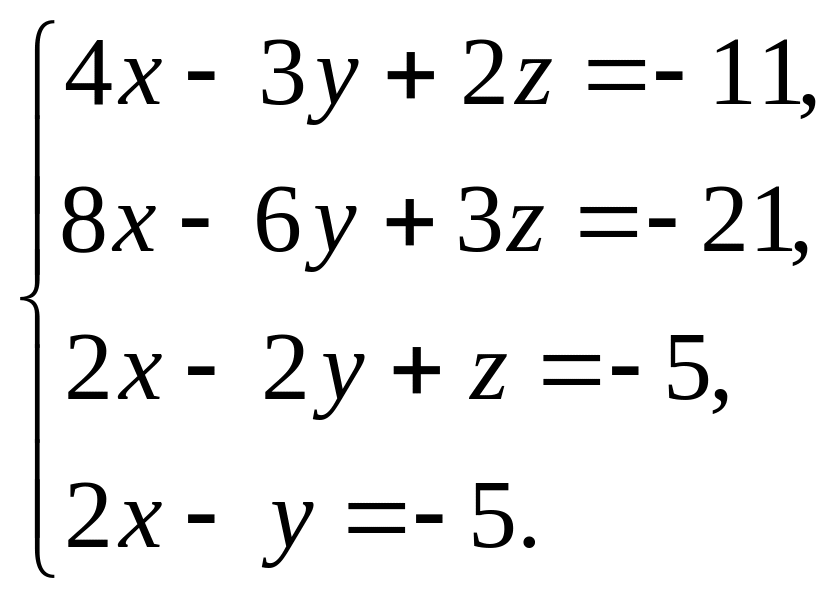 .
.
3.4.
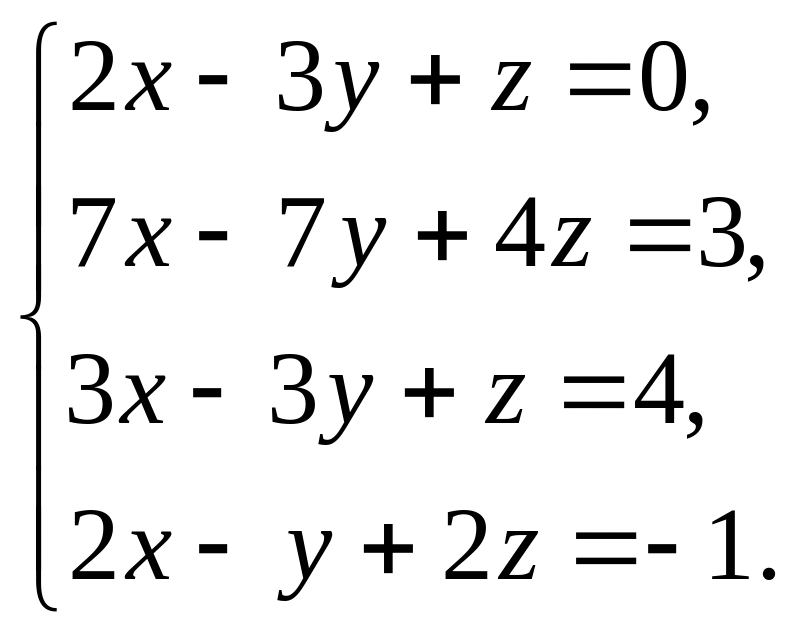 .
3.5.
.
3.5.
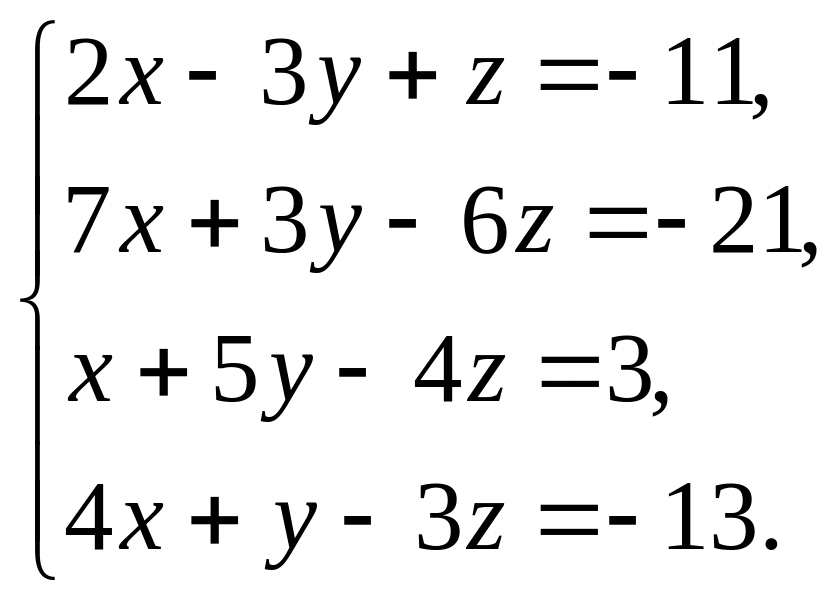 .
3.6.
.
3.6.
 .
.
3.7.
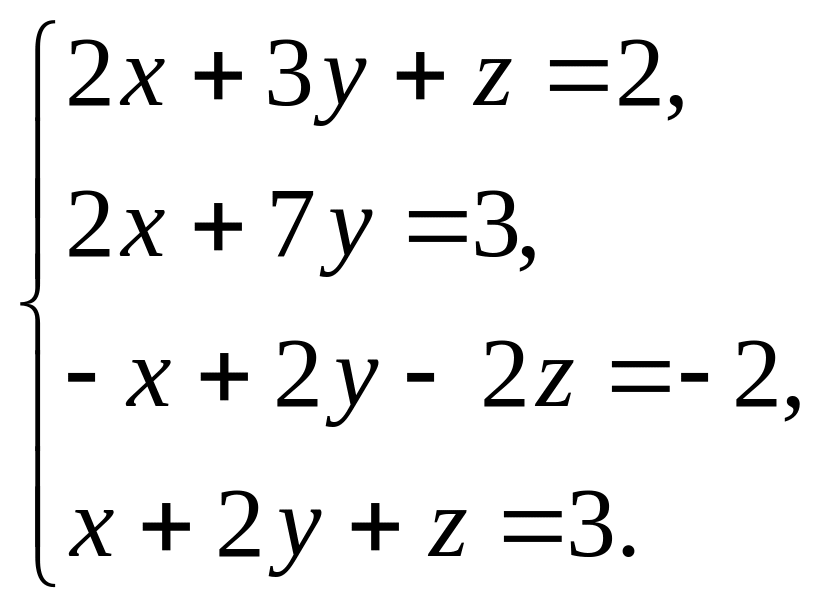 .
3.8.
.
3.8.
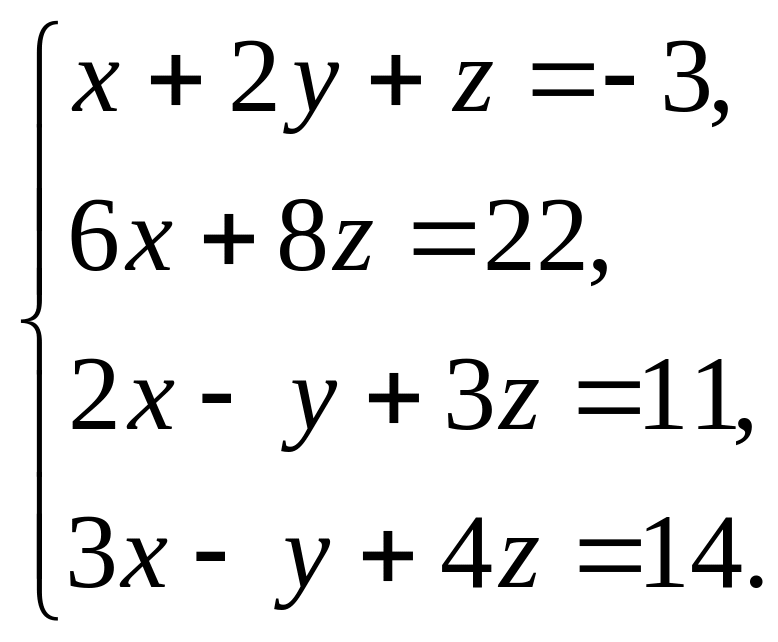 .
3.9.
.
3.9.
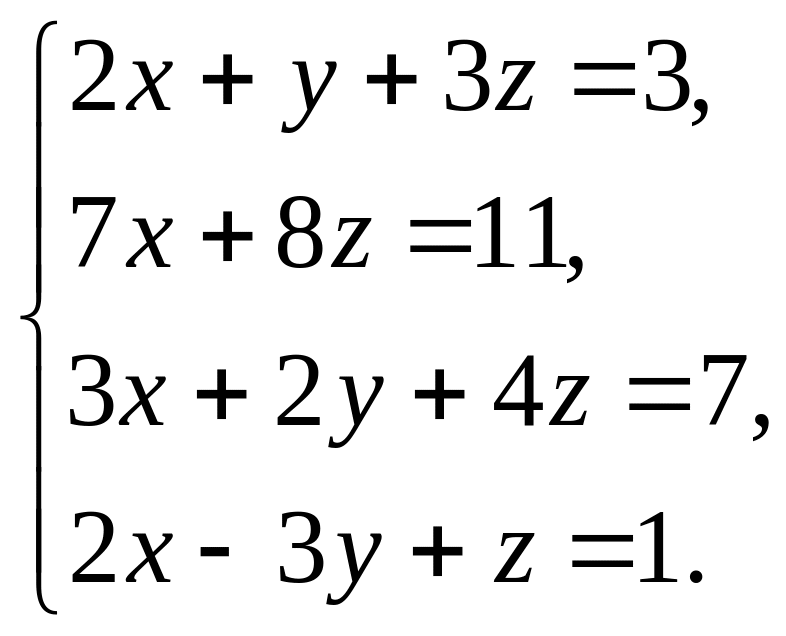 .
.
3.10.
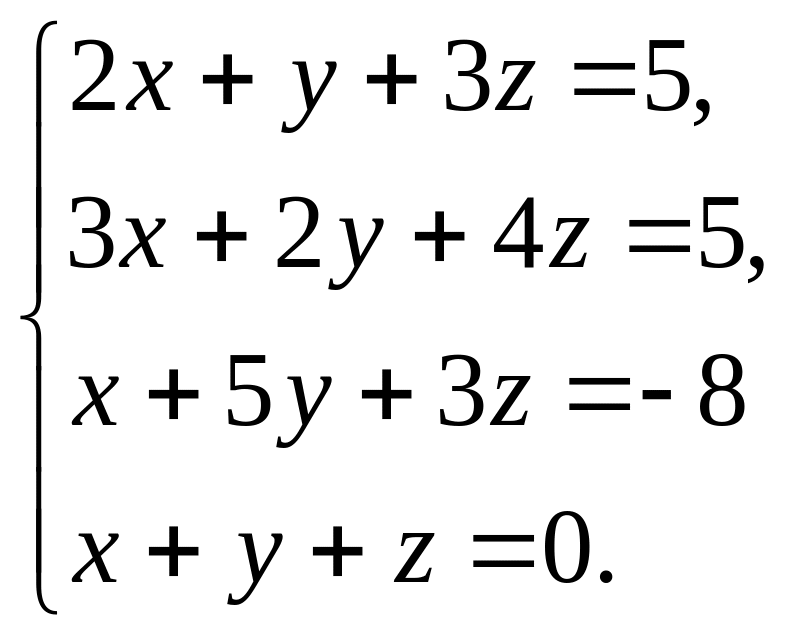 .
.
Векторная алгебра
ЗАДАЧА 4
Найти площадь и
длины диагоналей параллелограмма,
построенного на векторах
![]() .
.
4.1.
![]() .
.
4.2.
![]() .
.
4.3.
![]() .
.
4.4.
![]() .
.
4.5.
![]() .
.
4.6.
![]() .
.
4.7.
![]() .
.
4.8.
![]() .
.
4.9.
![]() .
.
4.10.
![]() .
.
ЗАДАЧА 5
Даны вершины треугольника А, В, С. Найти косинус угла ВАС, проекцию стороны АВ на сторону АС и площадь треугольника АВС.
5.1. A(1;–2;3); B(0;–1;2); C(4;0;4). 5.2. A(0;–3;6); B(–12;–3;–3); C(–9; –3;–6).
5.3. A(3;3;–1); B(5;5;–2); C(4;1; 1). 5.4. A(–1;2;–3); B(3;4;–6); C(1;1;–1).
5.5. A(–4;–2;0); B(–1;–2;4); C(3;–2;1). 5.6. A(5;3;–1); B(5;2;0); C(6;4;–1).
5.7. A(–3;–7;–5); B(0;–1;–2); C(-5;-6;-6). 5.8. A(3;3;–1); B(1;–5;2); C(4;4;1).
5.9. A(2;1;–1); B(6;–1;–4); C(4;2;1). 5.10. A(3;–6;9); B(0;–3;6); C(5;-3;7).
Задача 6
Вычислить объем тетраэдра с вершинами в точках A, B, C, D.
6.1. A(14;4;5), B(–5;–3;2), C(–2;–6;–3), D(–2;2;–1).
6.2. A(1;2;0), B(3;0;–3), C(5;2;6), D(8;4;–9).
6.3. A(2;–1;2), B(1;2;–1), C(3;2;1), D(–4;2;5).
6.4. A(2;–1;2), B(1;2;–1), C(3;2;1), D(–4;2;5).
6.5. A(1;1;2), B(–1;1;3), C(2;–2;4), D(–1;0;–2).
6.6. A(2;3;1), B(4;1;–2), C(6;3;7), D(7;5;–3).
6.7. A(1;5;–7), B(–3;6;3), C(–2;7;3), D(–4;8;–12).
6.8. A(–3;4;–7), B(1;5;–4), C(–5;–2;0), D(2;5;4).
6.9. A(–1;2;–3), B(4;–1;0), C(2;1;–2), D(3;4;5).
6.10. A(4;–1;3), B(–2;1;0), C(0;–5;1), D(3;2;–6).
Аналитическая геометрия задача 7
7.1. Даны вершины треугольника А(1;2), В(5;10), С(11;4). Найти уравнение высоты, опущенной из вершины В.
7.2. Даны вершина треугольника А(3;4), В(8;12), С(11;8). Найти уравнение медианы треугольника, проведенной из вершины В.
7.3. Даны вершины треугольника А(4;5), В(8,13), С(14;7). Найти координаты центра описанной около треугольника окружности.
7.4. Даны вершины треугольника А(–3;3), В(4;4), С(–1;12). Найти уравнение прямой, проходящей через точку В параллельно стороне АС.
7.5. Даны вершины треугольника А(1;1), В(7;9), С(–3;2). Найти длину высоты, опущенной из вершины С.
7.6.
Даны уравнения двух сторон прямоугольника
![]() ,
,
![]() и одна из его вершин А(1;–1).
Найти уравнения двух других его сторон.
и одна из его вершин А(1;–1).
Найти уравнения двух других его сторон.
7.7. Даны вершины треугольника А(0;1), В(4;9), С(10;3). Найти острый угол между высотой, опущенной из вершины А и стороной АВ.
7.8.
Найти проекцию точки Р(–8;2)
на прямую
![]() .
.
7.9. Даны две вершины треугольника А(–10;2), В(6;4). Его высоты пересекаются в точке D(5;2). Определить координаты третьей вершины С.
7.10.
Найти острый угол между прямой
![]() и прямой, проходящей через точки А(1;–1)
и В(5;7).
и прямой, проходящей через точки А(1;–1)
и В(5;7).
Задача 8
8.1.
Найти уравнение плоскости, проходящей
через точки
![]() .
.
8.2.
Найти уравнение плоскости, проходящей
через точки
![]() и параллельной оси ОХ.
и параллельной оси ОХ.
8.3.
Найти уравнение плоскости, проходящей
через точки
![]() и параллельной оси ОУ.
и параллельной оси ОУ.
8.4.
Найти уравнение плоскости, проходящей
через точки
![]() и параллельной оси ОZ.
и параллельной оси ОZ.
8.5.
Найти уравнение плоскости, проходящей
через точку
![]() и ось ОХ.
и ось ОХ.
8.6.
Найти уравнение плоскости, проходящей
через точку
![]() и ось ОУ.
и ось ОУ.
8.7.
Найти уравнение плоскости, проходящей
через точку
![]() и ось ОZ.
и ось ОZ.
8.8.
Найти уравнение плоскости, проходящей
через точку
![]() и перпендикулярной плоскостям
и перпендикулярной плоскостям
![]()
8.9.
Найти уравнение плоскости, проходящей
через точку
![]() и параллельной векторам
и параллельной векторам
![]() .
.
8.10.
Найти уравнение плоскости, проходящей
через начало координат и точки
![]() .
.
Задача 9
9.1.
Найти проекцию точки Р(6;4;7)
на плоскость
![]() .
.
9.2.
Найти проекцию точки Р(10;6;7)
на плоскость
![]() .
.
9.3.
Найти проекцию точки Р(–2;11;7)
на плоскость
![]() .
.
9.4.
Найти проекцию точки Р(10;7;–7)
на плоскость
![]() .
.
9.5.
Найти проекцию точки Р(–4;7;5)
на плоскость
![]() .
.
9.6.
Найти проекцию точки Р(2;–1;3)
на прямую
![]() .
.
9.7.
Найти проекцию точки Р(5;6;–9)
на прямую
![]() .
.
9.8.
Найти проекцию точки Р(5;5;–4)
на прямую
![]() .
.
9.9.
Найти проекцию точки Р(6;–16;5)
на прямую
![]() .
.
9.10.
Найти проекцию точки Р(3;2;6) на прямую
![]() .
.
