2. Представление графов в turbo prolog
Графы в Прологе могут представляться многими способами. Рассмотрим некоторые из них на модельном графе (рис. 8.2).
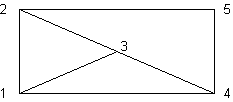
рис. 8.2
Первый способ — перечислить ребра графа в виде утверждений базы данных (для неориентированного графа каждое ребро повторяется дважды):
after(1,2). after(2,1). after(1,3). after(3,1).
after(1,4). after(4,1). after(2,3). after(3,2).
after(2,5). after(5,2). after(3,4). after(4,3).
after(5,4). after(4,5).
Однако, для многих алгоритмов более предпочтительным представлением являются СПИСКИ ИНЦИДЕНТНОСТИ (когда к каждой вершине прицеплен список соседок — смежных с ней вершин):
graph([1,2,3,4]).
graph([2,3,1,5]).
graph([3,1,2,4]).
graph([4,1,3,5]).
graph([5,2,4]).
Голова списка — сама вершина, хвост — список ее соседок.
Граф можно хранить в виде динамической структуры — списка списков — и передавать ее в качестве аргумента из процедуры в процедуру:
domains
uzl=integer
list=uzl*
llist=list*
<.............>
goal
Graph = [[1,2,3,4],[2,1,3,5],[3,1,2,4],[4,1,3,5],[5,2,4] ], <....>.
Для «нагруженных» графов, ребрам которых приписаны веса (или стоимости) нужно произвести некоторые изменения:
у предиката after появится третий аргумент — вес ребра:
after1(1,2,3).
after1(2,1,3). /* вес ребра 1-2 равен 3*/;
у предиката graph появится второй аргумент — список весов соответствующих ребер:
graph1([5,2,4], [5,1]).
/* вес ребра 5-2 равен 5, ребра 5-4 равен 1 */.
К динамическому списку списков, представляющему граф, нужно добавить еще один список списков — с весами соответствующих ребер.
Количество вершин и ребер графа можно запрашивать во время выполнения программы и передавать в качестве параметра, а лучше — хранить в виде утверждений базы данных:
num_reb(7).
num_uzl(5).
3. Поиск пути на неориентированном графе
Пусть требуется найти всевозможные пути между парой фиксированных вершин: началом(A) и концом(Z). Путь от A до Z будем хранить в виде списка вершин, где Z будет головой списка:
[Z|Solution]
Алгоритм с возвратом будет искать пути следующим образом:
— начальный путь будет состоять из единственной вершины [A];
— пусть текущий путь оборвался на вершине X. Чтобы продолжить текущий путь на один шаг, найдем соседку вершины X — вершину Y. Если она не принадлежит текущему пути, продолжим его до вершины Y:
[Y,X|Was] /* Was — текущий путь до вершины X */;
— если из очередной вершины Y попали в Z (нашли решение) или в тупик (у вершины Y нет допустимых соседок), то производим возврат:
вместо вершины Y находим другую допустимую соседку Y’ вершины X и продолжаем путь из Y’.
Дерево поиска, построенное алгоритмом с возвратом, показано на рис. 8.3.
рис. 8.3
Составим процедуру поиска пути way.Она будет иметь три аргумента:
вершина — конец пути; текущий (частичный) путь; решение (полный путь)
и состоять из двух правил: правила окончания рекурсии, когда путь заканчивается вершиной Z:
way(Z, [Z|Was], [Z|Was]).
и правила продолжения пути на один шаг с вызовом дальнейшей рекурсии
way(Z, [X|Was], Sol):-
sosed(X,Y),
not(member(Y,Was)),
way(Z, [Y,X|Was], Sol).
Все возможные пути будут получаться из-за недетерминированности процедуры sosed, которая при возвратах будет подставлять на место Y поочередно всех соседок вершины X.
/* Программа 8.3 «Поиск всех путей от A до Z» */
domains
uzl=integer
list=uzl*
predicates
graph(list)
show_way
way(uzl,list,list)
sosed(uzl,uzl)
member(uzl,list)
goal
show_way.
clauses
num_uzl(5).
graph([1,2,3,4]).
graph([2,1,3,5]).
graph([3,1,2,4]) .
graph([4,1,3,5]).
graph([5,2,4]).
show_way:-
write("Начало пути "), readint(A),
write("Конец пути "), readint(Z),
way(Z, [A], Solution), write(Solution),
nl, fail.
% путь окончился в Z
way(Z, [Z|Was], [Z|Was]).
way(Z, [X|Was], Sol):-
sosed(X,Y),
% Y не содержится в пути
not(member(Y,Was)),
% продолжили путь до Y
way(Z, [Y,X|Was], Sol).
sosed(X,Y):-
graph([X|T]), % T — список соседок X
% Y — принадлежит списку соседок X
member(Y,T).
member(H,[H|_]). % недетерминированная
member(X,[_|T]):- % процедура
member(X,T). % отыщет при возвратах
% всех соседок
/* Конец программы */
Процедура sosed обязана своей недетерминированностью процедуре member, входящей в ее состав. Эта процедура при возвратах будет пропускать первую вершину из списка соседок и искать соседку в хвосте списка.