9. Добавление и удаление элемента

Рассмотрим случай, когда элемент X добавляется к началу списка L:

add(X,L,[X|L])

Случай, когда элемент добавляется к концу списка, можно описать аналогично правилу conc:

вначале рассмотреть добавление X к пустому списку;

если список не пуст, то его элементы временно пересылаются в стек, а затем поочередно добавляются к голове списка [X].

Можно воспользоваться процедурой conc:

add_end(X, L, L1):-

conc(L, X, L1).

Удаление заданного элемента X из списка L описывается следующей недетерминированной процедурой:

del(X, [X|T], T).

del(X, [H|T], [H|T1]):-

del(X, T, T1).

Первое правило соответствует случаю, когда X совпадает с головой списка, второе — вызывает рекурсию для поиска X в хвосте. При возвратах будет удаляться каждый раз новое вхождение X. На внешний запрос del(2, [2,3,2,1]) система ответит

L=[3,2,1]

L=[2,3,1]

Упражнение 6.3.

1. Напишите процедуру удаления элемента из конца списка без использования процедуры conc.

2. Напишите процедуру удаления ВСЕХ вхождений элемента.

10. Подсписок

Составим процедуру, определяющую, является ли список S подсписком списка L:

sublist(S, L)

Б удем считать, что список L состоит из трех списков L1, S, L3, а списки S и L3 составляют список L2 (рис. 6.2).

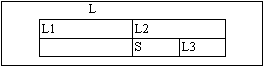
рис. 6.2

Отметим, что списки L1, S, L3 могут быть пустыми. Исходя из наглядных геометрических соображений, запишем правило принадлежности списка S списку L:

sublist(S, L):-

conc(L1, L2, L),

conc(S, L3, L2).

Это правило имеет чисто декларативный смысл. В нем утверждается, что если список L состоит из списков L1 и L2, и список L2 состоит из списков S и L3, то S есть подсписок L.

Интересно, что это правило может работать в обе стороны — если S является переменной, то правило генерирует всевозможные подсписки данного списка.

Упражнение 6.4.

Сгенерировать все подсписки списка [1,2,3], подавляя печать пустого списка [].

11. Перестановки списка

Составим процедуру, генерирующую всевозможные перестановки P заданного списка L:

perest(L, P)

Весь процесс можно представить себе в виде такой совокупности действий:

1. Отсекаем от списка голову H.

2. Переставляем хвост.

3. Вносим H в произвольное место переставленного хвоста.

Граничным условием рекурсии будет перестановка пустого списка:

perest([],[]).

Рекурсивное правило:

perest([X|T]):-

perest(T, T1),

into(X, T1, P).

Недетерминированная процедура вставки элемента в произвольное место списка выглядит так:

/* или X становится головой списка, или элементом хвоста */

into(X, L, [X|L]).

into(X, [H|T], [H|T1]):-

into(X, T, T1).

Упражнение 6.5.

Соберите в одну программу все рассмотренные нами правила работы со списками применительно к спискам из целых чисел.

Глава 7. Сортировка списков

1. Разделение списка на два

При работе со списками достаточно часто требуется разделить список на несколько частей. Это бывает необходимо, когда для целей текущей обработки нужна лишь определенная часть исходного списка.

Рассмотрим предикат div1, аргументами которого являются элемент данных и три списка:

div1(Middle,L,L1,L2)

Элемент Middle здесь является разделителем, L — это исходный список, а L1 и L2 — подсписки, получающиеся в результате деления списка L. Если элемент исходного списка меньше или равен Middle, то он помещается в список L1; если больше, то в список L2.

Предположим, что вначале значением переменной Middle является число 40, переменной L присвоен список [30,50,20,25,65,95], а переменные L1 и L2 свободные.

div1(40,[30,50,20,25,65,95],L1,L2)

Идея разделения следующая:

1. Извлекаем из списка голову H, а потом сравнивается с элементом Middle.

2. Если значение H меньше или равно значению Middle, то элемент помещается в список L1, в противном случае — в список L2.

3. Повторяем эту последовательность действий для хвоста.

В результате применения правила к списку [30,50,20,25,65,95] значениями списков L1 и L2 станут соответственно [30,20,25] и [50,65,95].

Само правило для разделения списка записывается следующим образом:

div1(_,[],[],[]):-!.

div1(Middle,[H|T],[H|T1],L2) :-

H <= Middle,!,

div1(Middle,T,T1,L2).

div1(Middle,[H|T],L1,[H|T2]) :-

div1(Middle,T,L1,T2).

Отметим, что метод деления списка на голову и хвост используется в данном правиле, как для разделения исходного списка, так и для формирования выходных списков.

Приведенное правило годится для любых базовых типов данных. Если список состоит из символических имен, то разделение будет происходить исходя из старшинства ASCII кодов.

/* Программа 7.1 «Деление списка». */

/* Назначение: Разделение списка на два. */

domains

list = integer *

predicates

div1(integer,list,list,list)

clauses

div1(_,[],[],[]):-!.

div1(Middle,[H|T],[H|T1],L2) :-

H <= Middle,

div1(Middle,T,T1,L2).

div1(Middle,[H|T],L1,[H|T2]) :-

div1(Middle,T,L1,T2).

/* Конец программы */