I уровень
1.1. Найдите число, логарифм которого по основанию 2 равен:
1) –2; 2) –1; 3)
4)
5)
6) 0;
7)
8)
9)
10)
11)
1; 12) 2.
1.2. Найдите логарифм числа 729 по основанию:
1) 9; 2) 3; 3)
4)
1.3. Найдите логарифм числа по основанию 3:
1) 1; 2) 3; 3) 9; 4) 27;
5)
6)
7)
8)
9)
10)
11)
12)
1.4. Найдите число b, если:
1)
2)
3)
4)
5)
6)
7)
8)
9)
1.5. Найдите число а, если:
1)
2)
3)
4)
5)
6)
1.6. Вычислите значение логарифма:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
1.7. Упростите выражение:
1)
2)
3)
4)
5)
6)
7)
8)
1.8. Вычислите:
1)
2)
3)
4)
5)
1.9. Прологарифмируйте выражение по основанию a:
1)
если
2)
если
3)
если
4)
если
5)
если
6)
если
7) Если
1.10. Выполните потенцирование:
1)
2)
3)
II уровень
2.1. Вычислите:
1)
2)
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)
13)
14)
15)
16)
2.2. Докажите неравенство:
1)
2)
2.3.
Известно,
что
Выразите
через
a
и
b
заданный логарифм:
1)
2)
3)
4)
III уровень
3.1. Вычислите:
1)
2)
3)
4)
3.2. Упростите выражение до числа:
3.3. Докажите, что
6.3. Логарифмическая функция
Логарифмической функцией называется функция
Свойства логарифмической функции
Область определения:
Множество значений:
Четность и нечетность: функция не обладает свойством четности.
Периодичность функции: непериодическая.
Нули: функция обращается в нуль при x = 1.
Промежутки знакопостоянства: если то функция положительна для
отрицательна для
если
то функция положительна для
отрицательна для
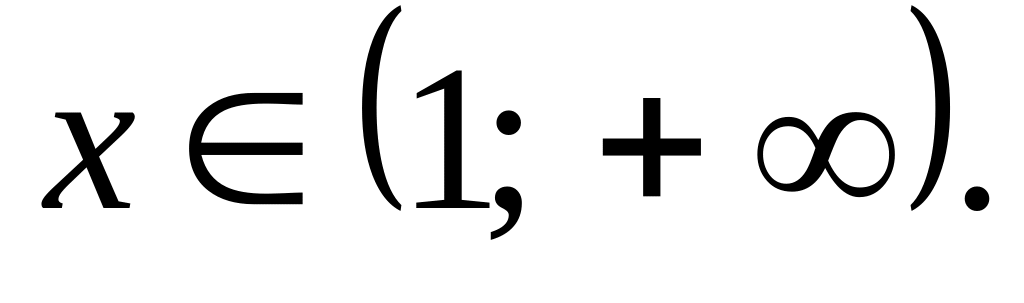
Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.
Промежутки возрастания и убывания: если функция убывает для
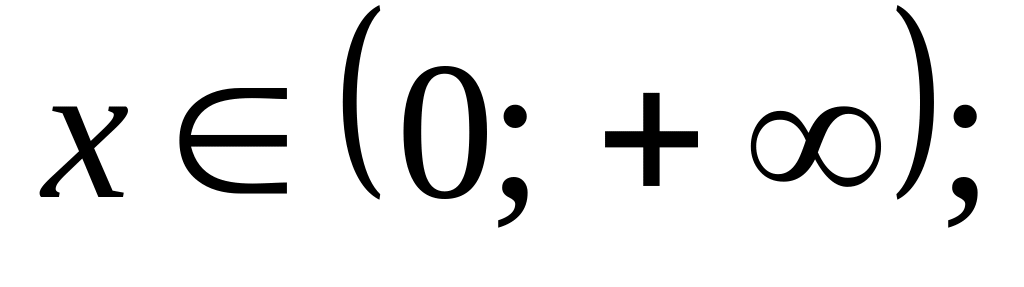если
возрастает для
Асимптоты: прямая x = 0 (ось Oy) – вертикальная асимптота.
График функции для
изображен на рис. 6.9, а для
на рис. 6.10.
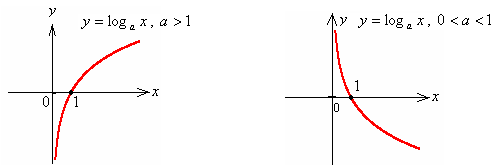
Рис. 6.9 Рис. 6.10
Из свойств функции
следует:
тогда и только тогда, когда
или
Функция
если
является обратной для функции
при
Функция если является обратной для функции при
Пример 1. Определить знак числа:
1)
2)
3)
4)
Решение.
1) Поскольку основание логарифма больше
1 (а = 7)
и значение, стоящее под знаком логарифма,
больше 1 (b = 35),
то из свойств логарифмической функции
2) Для основания
логарифма имеем
и для выражения, стоящего под знаком
логарифма, выполняется
Поэтому
3) Так как основание
логарифма 5 и 5 > 1, а выражение,
стоящее под знаком логарифма, равно
и
то
4) Для основания
логарифма выполняется
а под знаком логарифма число 19 (19 > 1).
Поэтому
Пример 2. Сравнить числа:
1)
и
2)
и
3)
и 3.
Решение. 1) Используем тот факт, что логарифмические функции с основанием 11 и 13 монотонно возрастают. Поэтому
Тогда
2) Рассмотрим числа
и
Так как
и
то
следовательно,
3) Известно, что
или
если a 0, b 0.
В нашем случае
тогда
т. е.
Пример 3.
Установить, между какими последовательными
целыми числами находится число
Решение. Поскольку логарифмическая функция с основанием 7 монотонно возрастает, то
Пример 4.
Найти функцию, обратную функции
Построить графики обеих функций в одной
системе координат.
Решение. Найдем функцию, обратную данной:
Построим графики функций:
а) строим график
функции
график функции
переносим параллельно на две единицы
вправо по оси Ox
и на две единицы вниз по оси Oy;
б) график обратной
функции
симметричен графику данной функции
относительно прямой
(рис. 6.11).
Рис. 6.11
Задания