
- •5. Степени и корни
- •5.1. Корень n-й степени
- •8) Где в случае
- •I уровень
- •II уровень
- •III уровень
- •5.2. Степень с произвольным действительным
- •I уровень
- •II уровень
- •III уровень
- •5.3. Степенная функция
- •I уровень
- •II уровень
- •III уровень
- •5.4. Иррациональные уравнения
- •I уровень
- •II уровень
- •III уровень
III уровень
3.1. Избавьтесь от иррациональности в знаменателе:
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]() 9)
9)
![]()
10)
![]() 11)
11)
![]() 12)
12)
![]()
13)
![]()
3.2. Упростите выражение:
1)
![]() 2)
2)

3)
![]() 4)
4)
![]()
5)
 6)
6)
![]()
7)
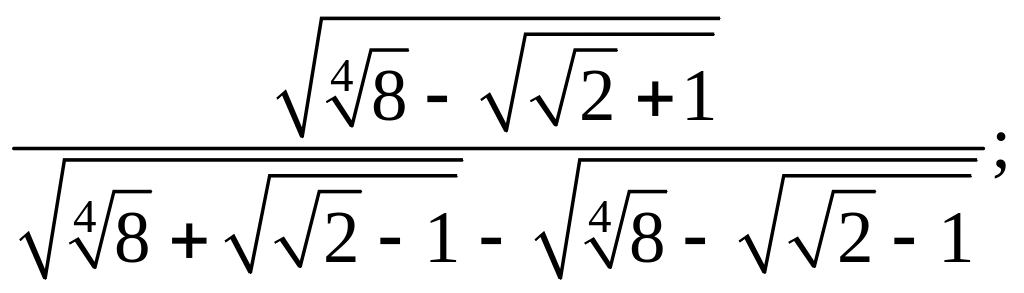 8)
8)
![]()
9)
![]()
10)
![]()
5.2. Степень с произвольным действительным
показателем
Во множестве R определена степень ax с действительным показателем.
В выражении ax число а называют основанием степени, число x – показателем степени. Нахождение значения степени называют возведением в степень.
Степень с действительным показателем
Пусть a R, тогда:
1)
![]() n
N;
n
N;
2)
![]()
3)
![]()
4)
![]() и a
0, если
и a
0, если
![]()
5)
![]() и если
и если
![]() то a
0;
то a
0;
6)
 и если
и если
![]()
7)
![]() где
где
![]() определяется следующим образом.
определяется следующим образом.
Пусть иррациональное
число k
записано в виде десятичной дроби,
![]() – последовательность его десятичных
приближений с недостатком (или с
избытком). Для любого действительного
числа а
0 степень
– последовательность его десятичных
приближений с недостатком (или с
избытком). Для любого действительного
числа а
0 степень
![]() с иррациональным показателем определяется
равенством
с иррациональным показателем определяется
равенством
![]()
На множестве R
не определены отрицательная и нулевая
степень числа 0, а также
![]() если
если
![]()
![]()
Свойства степеней
Допустим, что a, b, c R и это такие числа, что все степени имеют смысл. Тогда:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
5)
![]()
6) если a
> 1 и x
< y,
то
![]()
если 0 < a
< 1 и x
< y,
то
![]()
7) если 0 <
a
< b
и x
>0, то
![]()
если 0 < a
< b
и x
< 0, то
![]()
Пример 1.
Вычислить
![]()
Решение. Используем свойства степеней

Пришли к ответу:
![]()
Задания
I уровень
1.1. Представьте выражение в виде степени с рациональным показателем:
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
5)
 6)
6)
![]()
7)
![]() 8)
8)
![]()
9)
![]() 10)
10)
![]()
11)
![]() 12)
12)
![]()
13)
![]() 14)
14)
![]()
1.2. Выполните действия:
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
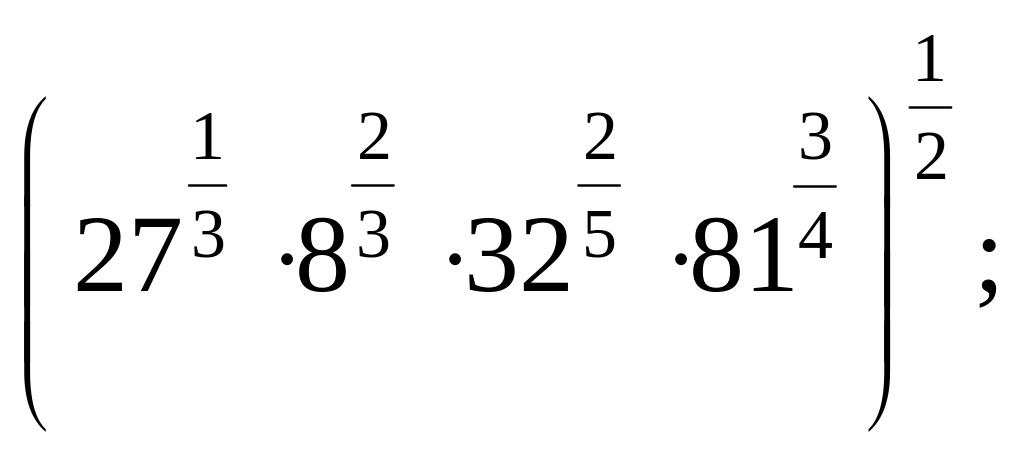
7)
![]() 8)
8)

9)

1.3.
Найдите
![]() из уравнения:
из уравнения:
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
1.4. Упростите выражение

II уровень
2.1. Вычислите:
1)

2)
![]()
3)
![]()
4)
![]()
5)
![]()
6)
![]()
2.2. Упростите выражение:
1)

2)

3)

III уровень
3.1. Вычислите:
1)
![]()
2)
![]()
3)
![]()
4)
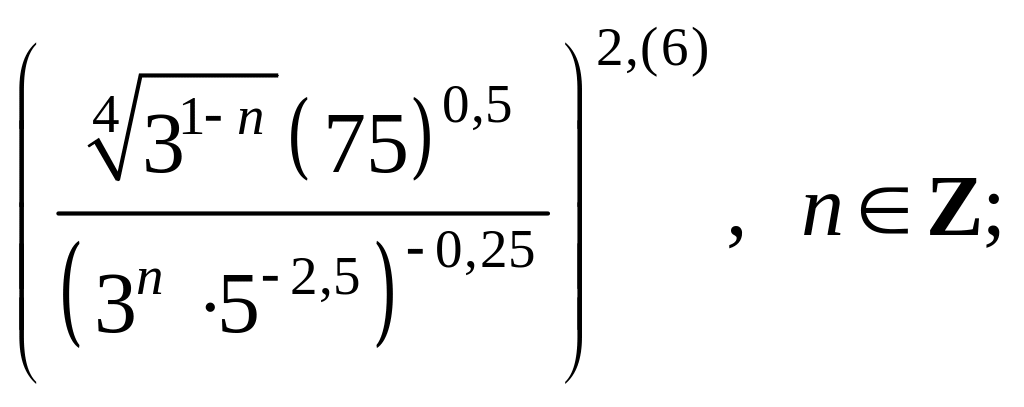
5)

3.2. Найдите значение выражения:
1)
 при
при
![]()
2)

5.3. Степенная функция
Функция
![]() где х
– переменная величина,
– заданное число, называется степенной
функцией.
где х
– переменная величина,
– заданное число, называется степенной
функцией.
Если
![]() то
то
![]() – линейная функция, ее график – прямая
линия (см. параграф 4.3, рис. 4.7).
– линейная функция, ее график – прямая
линия (см. параграф 4.3, рис. 4.7).
Если
![]() то
то
![]() – квадратичная функция, ее график –
парабола (см. параграф 4.3, рис. 4.8).
– квадратичная функция, ее график –
парабола (см. параграф 4.3, рис. 4.8).
Если
![]() то
то
![]() ее график – кубическая парабола (см.
параграф 4.3, рис. 4.9).
ее график – кубическая парабола (см.
параграф 4.3, рис. 4.9).
Степенная функция
![]()
Это обратная
функция для
![]()
Область определения:

Множество значений:

Четность и нечетность: функция нечетная.
Периодичность функции: непериодическая.
Нули функции: x = 0 – единственный нуль.
Наибольшее и наименьшее значения функции: наибольшего и наименьшего значений функция не имеет.
Промежутки возрастания и убывания: функция является возрастающей на всей области определения.
График функции симметричен графику кубической параболы относительно прямой y = x и изображен на рис. 5.1.

Рис. 5.1
Степенная функция
![]()
![]()
Область определения:
Множество значений:

Четность и нечетность: функция четная.
Периодичность функции: непериодическая.
Нули функции: единственный нуль x = 0.
Наибольшее и наименьшее значения функции: принимает наименьшее значение для x = 0, оно равно 0.
Промежутки возрастания и убывания: функция является убывающей на промежутке
 и возрастающей на промежутке
и возрастающей на промежутке

График функции (для каждого n N) «похож» на график квадратичной параболы (графики функций

 изображены на рис. 5.2).
изображены на рис. 5.2).

Рис. 5.2
Степенная функция
![]()
Область определения:
Множество значений:

Четность и нечетность: функция нечетная.
Периодичность функции: непериодическая.
Нули функции: x = 0 – единственный нуль.
Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет при любом
Промежутки возрастания и убывания: функция является возрастающей на всей области определения.
График функции (для каждого
 )
«похож» на график кубической параболы
(графики функций
)
«похож» на график кубической параболы
(графики функций
 изображены на рис. 5.3).
изображены на рис. 5.3).

Рис. 5.3
Степенная функция
![]()
Область определения:

Множество значений:

Четность и нечетность: функция нечетная.
Периодичность функции: непериодическая.
Нули функции: нулей не имеет.
Наибольшее и наименьшее значения функции: наибольшего и наименьшего значений функция не имеет при любом
Промежутки возрастания и убывания: функция является убывающей в области определения.
Асимптоты:
 (ось Оу)
– вертикальная асимптота;
(ось Оу)
– вертикальная асимптота;
![]() (ось Ох)
– горизонтальная асимптота.
(ось Ох)
– горизонтальная асимптота.
График функции (для любого n) «похож» на график гиперболы (графики функций
 изображены на рис. 5.4).
изображены на рис. 5.4).

Рис. 5.4
Степенная функция
![]()
Область определения:
Множество значений:

Четность и нечетность: функция четная.
Периодичность функции: непериодическая.
Наибольшее и наименьшее значения функции: наибольшего и наименьшего значений функция не имеет при любом
Промежутки возрастания и убывания: функция является возрастающей на
 и убывающей на
и убывающей на

Асимптоты: x = 0 (ось Оу) – вертикальная асимптота;
y = 0 (ось Ох) – горизонтальная асимптота.
Графиками функций являются квадратичные гиперболы (рис. 5.5).
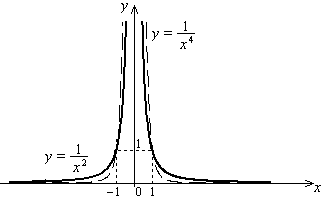
Рис. 5.5
Степенная функция
![]()
Область определения:

Множество значений:

Четность и нечетность: функция не обладает свойством четности и нечетности.
Периодичность функции: непериодическая.
Нули функции: x = 0 – единственный нуль.
Наибольшее и наименьшее значения функции: наименьшее значение, равное 0, функция принимает в точке x = 0; наибольшего значения не имеет.
Промежутки возрастания и убывания: функция является возрастающей на всей области определения.
Каждая такая функция при определенном показателе является обратной для функции
 при условии
при условии

График функции «похож» на график функции
 при любом n
и изображен на рис. 5.6.
при любом n
и изображен на рис. 5.6.

Рис. 5.6
Степенная функция
![]()
Область определения:
Множество значений:
Четность и нечетность: функция нечетная.
Периодичность функции: непериодическая.
Нули функции: x = 0 – единственный нуль.
Наибольшее и наименьшее значения функции: наибольшего и наименьшего значений функция не имеет при любом
Промежутки возрастания и убывания: функция является возрастающей на всей области определения.
График функции изображен на рис. 5.7.

Рис. 5.7
Пример 1. Построить график функции:
1)
![]() 2)
2)
![]()
Решение. 1) Для построения графика данной функции используем правила преобразования графиков:
строим график функции
 (он показан на рис. 5.7);
(он показан на рис. 5.7);график функции
 получаем из графика функции
путем параллельного переноса его на
одну единицу вправо по оси Ох
и на две единицы вниз по оси Оу;
получаем из графика функции
путем параллельного переноса его на
одну единицу вправо по оси Ох
и на две единицы вниз по оси Оу;график исходной функции получаем из графика функции
 оставляем ту часть графика, которая
находится справа от оси Оу
и на оси Оу,
другую – отбрасываем (на рис. 5.8 она
показана пунктиром). Оставшуюся часть
графика дополняем симметричной ей
относительно оси Оу
(рис. 5.8).
оставляем ту часть графика, которая
находится справа от оси Оу
и на оси Оу,
другую – отбрасываем (на рис. 5.8 она
показана пунктиром). Оставшуюся часть
графика дополняем симметричной ей
относительно оси Оу
(рис. 5.8).

Рис. 5.8
2) Преобразуем
функцию к виду
![]() Заметим, что
Заметим, что
![]() График этой функции получаем путем
следующих преобразований:
График этой функции получаем путем
следующих преобразований:
строим график функции

график
 получаем из предыдущего симметричным
отображением относительно оси Оу;
получаем из предыдущего симметричным
отображением относительно оси Оу;график функции
 получаем из предыдущего смещением на
4 единицы вправо по оси Ох;
получаем из предыдущего смещением на
4 единицы вправо по оси Ох;график заданной функции получаем из графика функции параллельным переносом его на две единицы вниз по оси Оу (рис. 5.9).

Рис. 5.9
Задания
