§23. Вынужденное рассеяние мандельштама-бриллюэна (врмб)

Примером нелинейного взаимодействия волн - электромагнитной и звуковой – является эффект ВРМБ. Известно, что при малых интенсивностях света происходит процесс рассеяния на флуктуациях плотности среды. Элементарный акт рассеяния электромагнитной волны на акустических колебаниях состоит из поглощения фотона, падающего на среду, и из одновременного испуская фотона рассеянного излучения и акустического фонона (стоксово рассеяние). Из законов сохранения энергии и импульса

(23.1)

,

где ; ; - векторы и частоты фотонов и фонона, следует, что смещение частоты составит величину:

, (23.2)

где - показатель преломления среды; и - фазовые скорости звука в среде и света в вакууме; - угол между векторами и (угол рассеяния).

Аналогичный сдвиг происходит при поглощении падающего фотона и акустического фонона и последующего рождения рассеянного фотона (антистоксово рассеяние). Таким образом, относительно несмещенной частоты рассеянного излучения (рэлеевское рассеяние) возникают две компоненты – дублет Мандельштама-Бриллюэна, а сам эффект носит название – спонтанное Мандельштама-Бриллюэна рассеяние. Заметим, что если аналогичное рассеяние излучения происходит с поглощением или испусканием оптического фонона, то эффект носит название – спонтанное комбинационное (рамановское) рассеяние.

При спонтанном рассеянии флуктуации плотности в среде не зависят от проходящей через нее световой волны, что характерно для достаточно малых интенсивностей.

Однако положение резко меняется при мощном когерентном излучении. Интерференция мощных световых волн – падающей и рассеянной – вызывает заметный эффект электрострикции, который приводит к усилению звуковых волн, а последние, в свою очередь, влияют на рассеяние излучения. Весь процесс становится нелинейным, а эффект называют – вынужденное рассеяние Мандельштама-Бриллюэна (ВРМБ)

Кратко изложим основные результаты использования теории ВРМБ в жидкости. Движение вязкой жидкости описывается уравнением Навье-Стокса:

, (23.3)

где и – плотность и скорость жидкости; - давление; и - сдвиговый и объемный коэффициенты вязкости; - внешняя сила, действующая на единицу объема жидкости ( в переменном электрическом поле) [2]:

(23.4)

Индекс “0” означает равновесное состояние. Эта сила вызывает изменение плотности среды, с учетом которого волновое уравнение для электромагнитного поля записывается в форме

, (23.5)

где есть отклонение от равновесной плотности. Полагая, что , можно провести линеаризацию уравнения (23.3). Учитывая также уравнение непрерывности и связь между давлением и плотностью ( , - скорость звука), получим

(23.6)

где ; . Чтобы учесть поглощение световой волны, введем в уравнение (23.5) дополнительное слагаемое с проводимостью, и представим уравнение в виде

. (23.7)

Уравнения (23.6) и (23.7) образуют замкнутую систему для электрического поля и давления при акустических колебаниях среды с учетом поглощения.

Будем искать решение для падающей и рассеянной световых волн в виде

(23.8)

а звуковую волну запишем так

(23.9)

Предположим, что падающая волна фиксирована по фазе и амплитуде, а для стоксовой и звуковой волн считаем и постоянными. Тогда после подстановки (23.8) и (23.9) в (23.6) и (23.7) получим систему однородных алгебраических уравнений для нахождения и , условие разрешимости которой приводит к дисперсионному уравнению

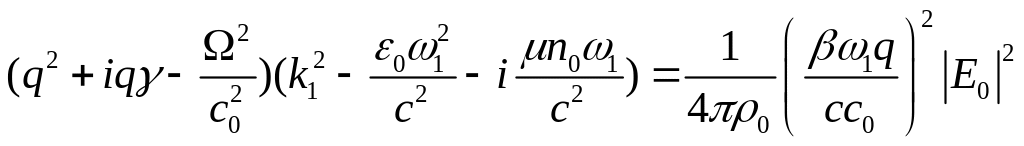, (23.10)

где введены обозначения

; , (23.11)

здесь - показатель преломления среды. Если , то получаем известные законы дисперсии для акустических колебаний и электромагнитных волн:

, ;

, . (23.12)

В общем случае при уравнение (23.10) представляет собой определение новых возбуждений в среде, которые невозможно разделить лишь на звуковую и электромагнитную ветви.

Вышеприведенный анализ показывает, что рассматриваемая задача взаимодействия световой и звуковой волн в некотором смысле аналогична задаче параметрического усиления. Поэтому должен существовать порог генерации стоксовой и звуковой волн.

Последующий анализ можно выполнить по той же методике, что изложена в § 21. Из дидактических соображений приведем этот анализ через укороченную систему уравнений. Покажем это на примере рассеяния назад, когда угол . За положительное направление возьмем направление стоксовой компоненты и будем искать решение уравнений (23.6) и (23.7) в виде

(23.13)

Допустим, что звуковая волна и волна накачки движутся в отрицательном направлении, тогда связь волновых векторов и частот можно представить в виде

(23.14)

Амплитуды , и представляют собой функции координаты и времени . Рассмотрим случай, когда они мало меняются на расстояниях порядка длин волн (звука и света) и за времена порядка периодов колебаний в волнах. Подставим в (23.13) в уравнения (23.6) и (23.7) и сохраним лишь первые производные по переменным. Получим систему уравнений

(23.15)

где введены коэффициенты поглощения.

Пусть . Решение системы уравнений ищем в виде

(23.16)

подставляя (23.16) в (23.15), получим систему алгебраических уравнений для нахождения и , условие разрешимости которой дает следующее дисперсионное уравнение:

, (23.17)

где . Обычно коэффициент поглощения звука относительно превосходит коэффициент поглощения света. В стационарном режиме ( ) при условии, что , уравнение (23.17) легко решается и дает два корня

,

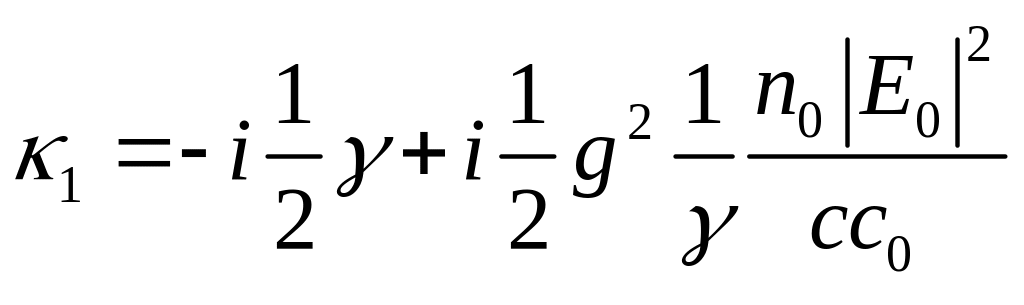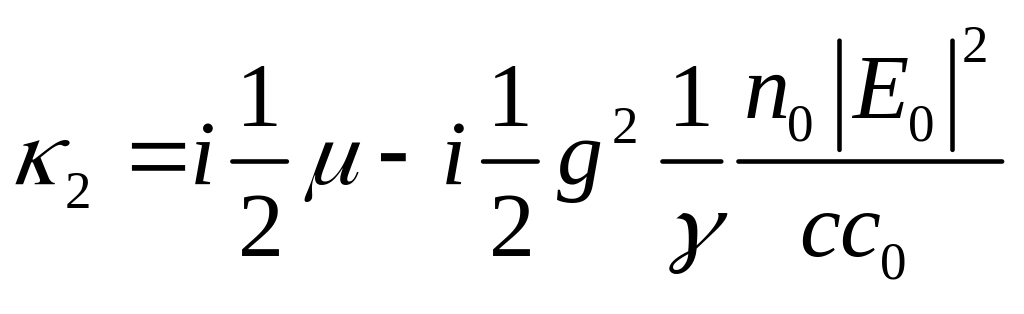, (23.18)

причем считаем также, что поле слабое ( ) . Из (23.18) следует, что поглощение стоксовой компоненты ослабляется, и при условии

(23.19)

возникает усиление, тогда как звуковая волна по-прежнему сильно поглощается.

ПРИЛОЖЕНИЕ

ПОСТУЛАТЫ КЛАСИЧЕСКОЙ МЕХАНИКИ

1.Материальная точка и траектория.

Материальной точкой считается любое тело, размерами которого можно пренебречь. Положение в пространстве и во времени определяется её радиус-вектором r=r(t),компоненты которого есть декартовы координаты x,y,z.Траектория представляет собой линию, описываемую в пространстве материальной точкой при своём движении.

2.Состояние механической системы

Состояние совокупности материальных точек (механической системы) полностью определяется заданием в некоторый момент времени всех координат и скоростей (скорость точки есть производная по времени от её радиус-вектора v=dr/dt).

3.Принцип относительности Галилея.

Существует бесконечное множество инерциальных систем отсчёта (в которых пространство является однородным и изотропным, а время-однородным), движущихся друг относительно друга равномерно и прямолинейно. Во всех инерциальных системах отсчёта законы механики одинаковы.

4.Уравнение движения.

Эволюция механической системы однозначно определяется её состоянием в начальный момент времени и динамическими уравнениями Ньютона:(d/dt)p=f, где p=mv есть импульс материальной точки, m-её масса, а f-сила, действующая на неё.

5.Критерий измеримости.

Не существует принципиальных ограничений на точность и одновременность измерения физических величин, определяющих динамику механических систем.

ПОСТУЛАТЫ НЕРЕЛЯТИВИСТКОЙ КВАНТОВОЙ МЕХАНИКИ

1.Критерий измеримости. Наблюдаемые

Измеримыми на опыте величинами (наблюдаемыми) являются собственные значения соответствующего данной физической величине линейного оператора. Измерение носит статистический характер, и каждое измерение даёт только одно из собственных значений. Искомые собственные значения и собственные функции находятся из уравнения вида: N|n>=n|n>, где n-собственное значение, |n>-собственная функция оператора N наблюдаемой. {Если наблюдаемая есть действительная величина, то оператор N -эрмитовый (N=N⁺), а его собственные функции |n> ортонормированы: (<n|m>=δ_nm) и образуют полную систему: (1=Σ_n |n><n| )}.

2.Принцип суперпозиции.

Динамическое состояние изолированной квантовой системы полностью определяется функцией состояния (x)=<x|ψ> (т.н. волновая функция, или пси-функция), где x обозначает совокупность координат частиц системы. Если волновая функция известна, то при измерении вероятность получить значение n равна: W_n=I<n|ψ>I², где амплитуда вероятности <n|ψ> находится из разложения волновой функции в ряд по собственным функциям наблюдаемой: |ψ>=_n | n><n|ψ>

.3.Уравнениие движения

Изменение во времени волновой функции (x),описывающей состояние кван­товой системы, определяется уравнением Шредингера

ih(d/dt) (x,t)=H(x,t)

где h-постоянная Планка, а H есть оператор полной энергии системы (называемый Гамильтонианом).