
- •Занятие №1 Основы дифференциального исчисления. Производная функции
- •1.1. Таблица некоторых производных элементарных функций.
- •1.2. Правила дифференцирования
- •1.3. Примеры нахождения производных
- •1.4. Найти производные функций
- •1 .5. Решить задачи
- •Занятие №2. Экстремумы функций. Дифференциал функции. Частные производные и полный дифференциал
- •2.1. Примеры и задачи с решениями.
- •2.2. Задания на самостоятельную работу
- •3.7. Задания на самостоятельную работу
- •Занятия №4 и №5. Дифференциальные уравнения
- •Основные определения
- •Примеры решения дифференциальных уравнений методом разделения переменных
- •Примеры решения задач, требующих составления дифференциальных уравнений
- •5.1. Задания на самостоятельную работу
- •Занятие №6. Элементы теории вероятности
- •6.1 Основные определения
- •6.2. Примеры решения задач
- •6.3. Задания на самостоятельную работу
- •Занятие №20. Электропроводимость биологических тканей и жидкостей Лабораторная работа: «Определение зависимости импеданса биологической ткани от частоты тока»
- •20.1. Ток в электролитах
- •20.2. Особенности электропроводимости биологических тканей
- •20.3. Гальванизация и лекарственный электрофорез.
- •20.4. Полное сопротивление (импеданс) цепи переменного тока
- •20.5. Электропроводимость биологических тканей для переменного тока. Импедансные методы в биологических и медицинских исследованиях
- •Порядок выполнения лабораторной работы
- •20.7. Задания на самостоятельную работу
20.4. Полное сопротивление (импеданс) цепи переменного тока
Электропроводимость и сопротивление электрической цепи для переменного тока зависят от вида нагрузок, входящих в состав этой цепи.
1) Если источник переменного напряжения
замкнут активным сопротивлением
![]() ,
то сдвиг фазы между силой тока через
эту нагрузку и напряжением на ней равен
нулю, а величина сопротивления нагрузки
не зависит от частоты тока.
,
то сдвиг фазы между силой тока через
эту нагрузку и напряжением на ней равен
нулю, а величина сопротивления нагрузки
не зависит от частоты тока.
2) Для конденсатора емкости С, замыкающего
источник переменного напряжения частоты
ω, в цепи переменного тока возникает
сдвиг фаз
![]() между током и напряжением. Причем на
емкостной нагрузке ток по фазе опережает
напряжение. Возникающее в такой цепи
емкостное сопротивление
между током и напряжением. Причем на
емкостной нагрузке ток по фазе опережает
напряжение. Возникающее в такой цепи
емкостное сопротивление
![]() обратно пропорционально частоте тока:
обратно пропорционально частоте тока:
![]() .
.
3) Если к источнику переменного напряжения подключена катушка индуктивности L, то наряду с активным сопротивление проводника катушки возникает индуктивное сопротивление XL, прямо пропорциональное частоте тока: XL = L ω. В такой электрической цепи возникает сдвиг фаз между током и напряжением, причем, ток по фазе отстает от напряжения на 900.
4) Когда электрическая цепь включает все три вида нагрузок, соединенных последовательно, то ее импеданс Z определяется соотношением:
![]() ,
,
а сдвиг фаз выражается формулой:
 .
.
20.5. Электропроводимость биологических тканей для переменного тока. Импедансные методы в биологических и медицинских исследованиях
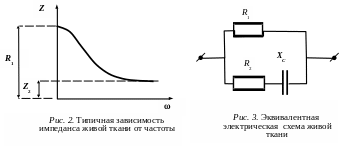
Измерения полного сопротивления (импеданса) биологической ткани, проведенные на разных частотах, показывают, что сопротивление ткани максимально и равно Z1= R1 на постоянном токе (ω = 0), а с увеличением частоты переменного тока импеданс сначала быстро уменьшается, а затем, достигнув некоторого значения Z2, остается практически постоянным (рис. 2). Такая зависимость импеданса от частоты объясняется наличием в ткани элементов, обладающих омическим и емкостным сопротивлением. Заметной индуктивностью биологические ткани не обладают. Простейшая эквивалентная электрическая схема живой ткани, дающая такую частотную зависимость, представлена на рисунке 3.
.
Емкостное сопротивление ткани
![]() определяется ее диэлектрическими
структурными составляющими (клеточными
мембранами, жировой клетчаткой,
эпидермисом), а величина сопротивлений
R1 и R2
(причем R1>>R2)
— омическими составляющими проводящих
структур биологической ткани (кожи,
тканевой жидкости, крови, цитоплазмы и
др.).
определяется ее диэлектрическими
структурными составляющими (клеточными
мембранами, жировой клетчаткой,
эпидермисом), а величина сопротивлений
R1 и R2
(причем R1>>R2)
— омическими составляющими проводящих
структур биологической ткани (кожи,
тканевой жидкости, крови, цитоплазмы и
др.).
В представленной на рисунке 9 эквивалентной схеме постоянный ток может идти только через сопротивление R1, т. к. сопротивление емкости С для него бесконечно велико. Но для переменного тока сопротивление емкости уменьшается с увеличением частоты, а с ним уменьшается и полное сопротивление цепи. На очень высоких частотах сопротивление емкости стремится к нулю (Хс 0), а импеданс — к наименьшему значению, определяемому формулой:
![]() . (3.2)
. (3.2)
Следует иметь в виду, что каждая ткань характеризуется своими значениями параметров R1, R2 и С эквивалентной схемы. Например, для кожи активное сопротивление на постоянном токе очень велико и составляет R1 ~ 104–106 Ом, а на высоких частотах падает в 10–20 раз. Для мягких кровенаполненных тканей R1 мало (R1 ~ 102 Ом) и меньше их емкостного сопротивления на низких частотах, поэтому часто эквивалентные схемы мягких тканей представлены только их активным сопротивлением R1.
На средних и высоких частотах, для которых Хс<<R1, сопротивление нижней ветви цепи (рис. 3), состоящей из R2 и Х2, будет значительно меньше R1, и основной ток будет идти по нижней ветви, поэтому на этих частотах импеданс цепи можно приближенно выразить упрощенной формулой
![]() (3.3)
(3.3)
Зависимость импеданса ткани от частоты переменного тока определяется физиологическим состоянием и морфологическими особенностями ткани, что позволяет использовать измерения их электропроводимости в биологических и медицинских исследованиях. Методы измерения электропроводимости тканей осуществляются при достаточно низких напряжениях (менее 50 мВ) и слабых токах, которые не повреждают ткани и не вносят изменений в их физико-химические процессы.
При действии повреждающих факторов (повышенной температуры, мощного ультразвука, ионизирующих излучений и др.), а также при отмирании ткани, происходит частичное или полное разрушение мембран. Эти процессы приводят к уменьшению роли емкостного сопротивления ткани и зависимость ее импеданса от частоты становится слабой. Поэтому по частотной зависимости импеданса можно оценивать жизнестойкость тканей организма, в частности, для оценки качества трансплантанта при пересадке тканей и органов
На регистрации импеданса тканей, изменяющегося с частотой сердечных сокращений, основан важнейший метода исследования состояния сосудистой системы – импедансная плетизмография (реография). Омическое сопротивление тканей сильно зависит от степени их кровенаполнения. Ткани неоднородны по своей структуре, а ток всегда идет по пути с наименьшим электрическим сопротивлением и прежде всего – по кровеносным сосудам, так как кровь имеет малое удельное сопротивление. Поэтому при увеличении кровенаполнения ткани ее омическая составляющая R импеданса уменьшается, а при уменьшении кровенаполнения – увеличивается. Таким образом, периодическая зависимость импеданса ткани от времени характеризует изменяющуюся степень кровенаполнения тканей, определяемую работой сердца и состоянием сосудистой системы. Регистрация реограмм имеет важное диагностическое значение.
