2. Вычисление пройденного пути

Из соотношения (6) следует, что при малых Δt приближенно выполняется: (7).

Равенство (7) выполняется тем точнее, чем меньше промежуток Δt. Если известно, как скорость зависит от времени, можно вычислить путь, пройденный МТ с момента времени t₁ до момента t₂. Если разбить промежуток времени на N малых промежутков: Δt₁, Δt₂,..., Δt_N. Весь путь s также представим как сумму путей, проходимых за соответственные промежутки Δt_i: Δs₁, Δs₂,..., Δs_N, так что выполняется: (8). Используя (7), можно приближенно представить: (9), где – значение скорости на промежутке Δt_i. Подставляя (9) в (8), получим: (10).

В пределе при стремлении к нулю всех промежутков Δt_i сумма, стоящая в правой части (10), будет точно равна пути: (11). Скорость есть функция времени . В математическом анализе в общем виде для произвольной функции f(x) задают определенный интеграл следующим образом: (12).

Тогда путь, пройденный МТ за промежуток времени от t₁ до t₂, равен определенному интегралу: (13).

Согласно определению геометрического смысла интеграла, путь, пройденный МТ за промежуток времени от t₁ до t₂, численно равен площади фигуры, ограниченной графиком функции , осью времени t и прямыми t₁ и t₂ (Рис. 5).

Рис. 5. Геометрическая интерпретация пути

Равномерное движение – это движение, при котором скорость, изменяясь как угодно по направлению, не меняется по величине. Тогда все значения в формуле (11) будут одинаковыми, и общий множитель можно вынести за знак суммы, при этом сумма временных промежутков равна времени t. Получаем: 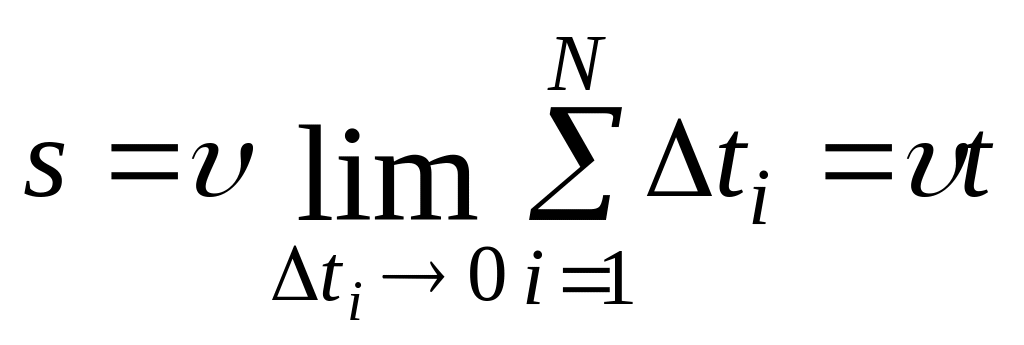(14).

Из (14) следует, что при равномерном движении скорость равна пути, деленному на время: (15).

3. Ускорение

Ускорение – это быстрота изменения скорости МТ со временем, характеризуется величиной: (16).

Если известны ускорение как функция времени и начальная скорость , то можно найти скорость МТ в любой момент времени: (17).

Если ускорение постоянно (движение МТ равноускореннное), то из (17) следует: (18).

При прямолинейном движении вектор скорости все время направлен вдоль одной и той же прямой – траектории, вследствие чего направление вектора ускорения совпадает с вектором скорости или противоположно ему. Если вектор ускорения параллелен вектору скорости, то скорость растет и движение будет ускоренным. Если вектор ускорения антипараллелен вектору скорости, то скорость уменьшается и движение будет замедленным. Прямолинейное движение с постоянным ускорением называют равнопеременным. Взяв соотношение для скорости в проекции на ось х так, что эта ось совпадает с начальной скоростью, имеем: (19).

Проекции , , a_x равны модулям соответствующих векторов, взятых со знаком "плюс", если направление вектора совпадает с осью х, взятых со знаком "минус", если направление вектора противоположно оси х. Интегрируя функцию (19) в пределах от нуля до произвольного момента времени t, получим формулу для пути при равнопеременном движении: (20).